标签：input   原来   有序   探讨   处理   图片   inf   位置   基本   

前言

想象一种现实场景，几个人打扑克牌，在接牌过程中，假设按照扑克牌上的数字大小进行摆牌，假设手中已经有若干张扑克牌（按照牌面大小排好次序），那么下次接到牌之后，我们会把刚接到的牌插入到手中已有的牌序列中的"合适"位置，现实中的这种"接牌"思路，就是我们今天要说的"插入思想"

直接插入排序算法

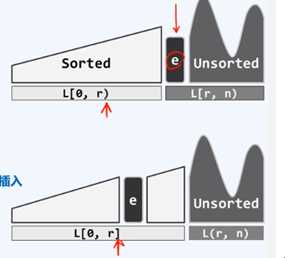
给定一个长度为n的序列L，如何用"接牌"思路把它拍好序呢？我们知道，排序算法涉及的两个基本操作：比较和移动元素。如果序列A是数组，我们会采用"就地排序"(in-place sort),即始终将序列A看做两部分 Sorted+Unsorted L[0,r)+L[r,n),初始化时 |S|=r=0为空序列无所谓有序。在迭代过程中，关注并处理e=L[r],在S中确定适当位置（有序序列中查找），插入e，得到有序序列L[0,r]。

不变性：随着r的递增，L[0,r）始终有序，直到r=n，L即为整体有序。

单调性：初始时，问题规模为n，即无序区间长度为n，有序区间长度为0，随着r的递增，有序序列向右扩展，无序序列区间相应缩小（减治法策略），直至最终整体有序，满足单调性

代码实现

1. void insertionsort(int A[], int lo, int hi)//插入排序 A[lo,hi)
2. {
3.    for (int i = lo + 1; i < hi; ++i)//无序序列每次取第一个元素插入有序序列中
4.    {
5.       int e = A[i]; //有序序列A[lo,i),无序序列A[i,hi),取A[i]插入有序序列合适位置
6.       int j = i - 1;
7.       for (; j >= lo; --j)//从有序序列末尾元素A[i-1]开始，逐步向前取元素与e比较
8.       {
9.          if (A[j] > e) //滚动数组，将比e大的元素向右移一个单位
10.             A[j + 1] = A[j];
11.          else//找到第一个不小于e的最大位置的元素，则结束循环
12.             break;
13.       }
14.       A[j+1] = e; //注意，位置j是不待遇e的最大秩，因此插入元素额要在j之后
15.    }
16. }

分析

算法最好情况下，待排元素全部有序，这样只需比较n-1次，每次比较之后，待插入元素e仍处在原来位置，时间复杂度O(n)，算法最坏情况下，待排元素全部逆序，这样在插入元素时，需要比较1+2+3+4+…+n-1=，同时移动元素次数也是，这样时间复杂度为O(n²)，平均复杂度也为O(n²)

由于在排序过程中，插入元素位置是满足插入依然有序的，即严格意义的大于，所以插入排序算法是稳定的排序算法。

运行结果

为了便于理解，可以将在有序向量中查找不大于元素e的位置和插入元素e这两个步骤分别编成函数，

代码实现2

1. void insertionsort_B(int A[], int lo, int hi)//A[lo,hi)插入排序
2. {
3.    for (int i=lo+1;i < hi;++i)
4.    {
5.       int e = A[i];
6.       int index = search(A, e, lo, i);//在A[lo,i)中查找不大于e的元素下标
7.       for (int j = i - 1; j > index; j--)//将A[index+1,i)元素整体向右移一个单元A(index+1,i]
8.          A[j + 1] = A[j];
9.       A[index + 1] = e;//插入元素e
10.    }
11. }
12. int search(int A[], int e, int lo, int hi)//在向量A[lo,hi)中查找不大于元素e的最大秩并返回
13. {
14.    while (--hi >= lo)
15.       if (A[hi] <= e) //这样如果有多个元素与e相等，则返回最大秩
16.          return hi;
17.    return hi;//此时hi=lo-1，即有序区间越界了
18. }

探索&深究

我们看到，插入排序的时间复杂度不仅与问题的规模n有关，而且与输入序列的逆序对总数I也息息相关，这种输入敏感型算法input-sensitive在排序算法中有着特殊地位。从上面的有序向量查找过程中，我们可以看到，insert（search（A，e）+1，e）这条语句仍然会保持有序向量A的有序性，这得益于我们的search每次返回的都是不大于e的最大秩，即使有序向量中有多个重复元素e，仍然会返回e的最大秩，这样才保证插入不破坏有序性。

创新性思维

    既然向量A是有序的，那么我们采用二分法查找不是更能快速得到结果吗？二分查找使得查找成功的平均时间性能为O(logn)比起顺序查找的O(n)有很大提高，下一篇我将着手探讨有序序列的二分查找奥秘！

排序算法之插入排序

标签：input   原来   有序   探讨   处理   图片   inf   位置   基本   

原文地址：https://www.cnblogs.com/gaochaochao/p/9256596.html