logistic回归学习和C++实现

标签：输出   类别   begin   构造   技术   思想   ++   类方法   先来   

logistic回归是一种分类方法，用于两分类的问题，其基本思想为：

1. 寻找合适的假设函数，即分类函数，用来预测输入数据的结果；
2. 构造损失函数，用来表示预测的输出结果与训练数据中实际类别之间的偏差；
3. 最小化损失函数，从而获得最优的模型参数。

首先来看一下sigmoid函数：

\(g(x)=\frac{1}{1-e^{x}}\)

它的函数图像为：

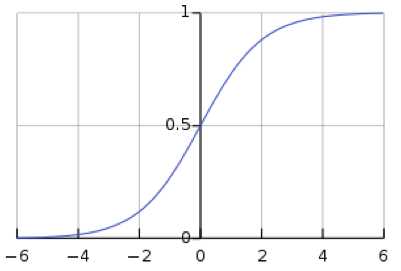
logistic回归中的假设函数（分类函数）：

\(h_{\theta }(x)=g(\theta ^{T}x)=\frac{1}{1+e^{-\theta ^{T}x}}\)

解释：

\(\theta \) —— 我们在后面要求取的参数；

\(T\) —— 向量的转置，默认的向量都是列向量；

\(\theta ^{T}x\) —— 列向量\(theta\)先转置，然后与\(x\)进行点乘，比如：

\(\begin{bmatrix}1\\ -1\\ 3\end{bmatrix}^{T}\begin{bmatrix}1\\ 1\\ -1\end{bmatrix} = \begin{bmatrix}1 & -1 & 3\end{bmatrix}\begin{bmatrix}1\\ 1\\ -1\end{bmatrix}=1\times 1+(-1)\times1+3\times(-1) = -3\)

logistic回归学习和C++实现

标签：输出   类别   begin   构造   技术   思想   ++   类方法   先来   

原文地址：https://www.cnblogs.com/tuhooo/p/9296915.html