标签:img 技术分享 一个 相同 margin 代码 方向 介绍 str
本篇博客我会重点介绍对红-黑树的理解,重点介绍红-黑树的查找,这里我们将要讨论的算法称为自顶向下插入,也就是把沿着树向下查找插入点
平衡树和非平衡树:当插入一组数据关键字是按照升序或者降序插入的话此时就是集中最极端的不平衡树,此时也可看做是一个链表此时对于此树的查找的时间复杂度为O(N),所以搜索不平衡树的时间复杂度介于平衡树时间复杂度O(logN)和O(N)之间时间具体取决于树的不平衡度。
接下来我们要讨论的红-黑树具有以下几个特征(红-黑树规则):
第四条中的“空子节点”指的是有右子节点的节点可能接左子节点的位置,或者说有左子节点的节点可能接右子节点的位置。就是非叶节点本可能有,但是实际上没有的那个子节点(若节点只有右子节点,那么空缺的左子节点就是空子节点,反之亦然)下图中50→25→25的右子节点(空子节点)黑色高度为1,从根到6以及到75的黑色节点数都为2,这样就违背了规则4,此树到叶节点的黑色节点数相同,但是有一个空子节点的黑色节点数为1所以此树不是红-黑树。
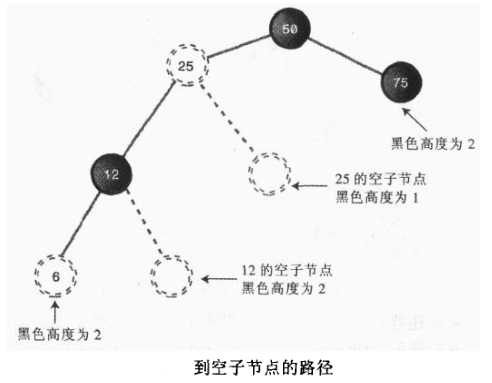
从根节点到叶节点路径上面的黑色节点数目称为黑色高度,所以上面的规则四的另一种陈述方法是:所有从根到叶节点路径上的黑色高度必须相同。
为了满足红黑树规则我们可能会使用到下面两种方式来进行修正,从而使一棵树满足红黑树规则,
为什么保证上面四个红-黑树规则就能保证红-黑树是平衡树呢?从红黑树规则分析我们可以得到若一棵树超过了两层不平衡怎这棵树则不可能满足红-黑树规则,超过两层不平衡则表明有路径的节点数比另外的路径的节点数多一个以上,多出来的要么有更多的黑色节点,若这样则违背了红-黑树规则4,要么至少有两个相邻接的红色节点,这样就违背了红色节点的子节点必须全部是黑色节点。
利用树的旋转来重新排列一些节点,来平衡一棵树,旋转必须要做到两件事情:
上面利用红黑树的颜色规则和节点的颜色变化只是有助于决定何时执行旋转。光改变颜色并不能让分树达到平衡,旋转才是让树平衡的关键操作,所以我们要好好理解树的旋转操作;做旋转的时候要注意做右旋顶点必须要有一个左子节点,左旋顶端必须要有右子节点,不然旋转后顶点会没有节点,接下来我们看下图的一个简单的旋转:
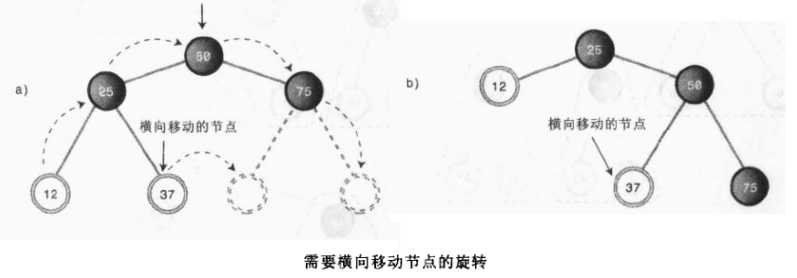
上图中a→b我们可以看到该树进行了一次右旋,a图中节点37称为顶端节点50的内侧子孙(节点12是外侧子孙点),对内侧子孙而言,如果他是上移的节点的子节点,它就必须要断开和父节点的连接并且重新连接到它以前的爷爷节点之上,就好像自己成为了自己的叔叔一样。上图是旋转过程中单节点的位置变换,上面我们说的内侧子孙也可以是一棵子树,下图我们展示了假如是子树的节点的一个移动情况,大致的原理差不多是相通的。
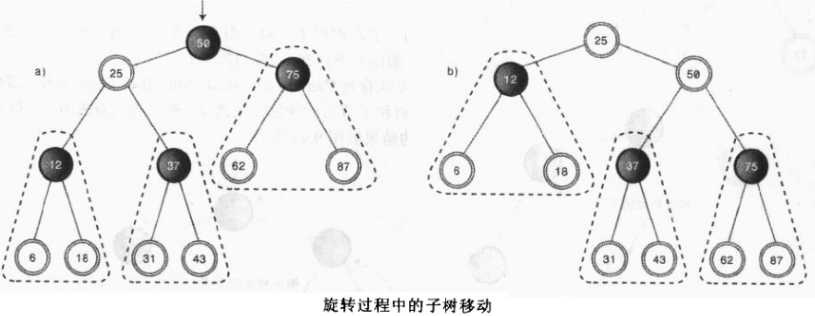
上图中的树进行了一次右旋,做了以下几个事情:
上面我们看到了旋转一棵树要进行怎么样的旋转,接下来我们讨论如何插入一个新节点(利用旋转和颜色规则来保持树的平衡)
在我们向下查找插入点的时候我们主要讨论一下三个方面
首先我们讨论下行途中的颜色变化查找的方式和普通的二叉搜索树是一样的,只是在下行的途中会涉及到颜色的变化,规则如下:每当遇到一个有两个红色子节点的黑色节点时,它必须把子节点变为黑色,把父节点变为红色(除非父节点为根节点),如下图就进行了一次颜色变换
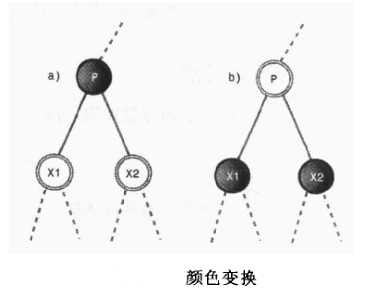
上图中进行颜色变化没有改变从根向下过P到叶节点或空子节点路径上的黑色节点的数目因此颜色变换并没有违反规则4,这样变化的好处是在不违背规则3的情况下连接新的红色节点更容易。上面颜色变化虽然不会违背规则4但是有可能违背规则3,若上图中P节点的父节点是红色,那么变换之后就违背了规则3,那么此时就会对树进行旋转操作,
向下路径上的旋转有两种可能性,当违背的节点是外侧的子孙节点“违背规则的节点”是指在造成红红冲突的父子节点对中的子节点,我们从50开始创建一棵新树插入以下节点:25,75,12,37,6和18在插入12和6的时候需要做颜色变换。接下来我们要插入节点3,必须对节点12以及它的子节点6和18做颜色变换,此时生成的树就是下图中的a树,此时节点25和12违背了红黑树规则3,此时需要对此树进行旋转的操作,
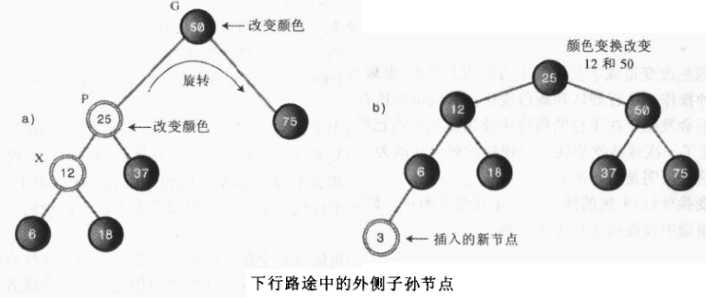
这里我们设刚刚进行颜色变换的三角形的顶点为X,X的父节点为p,祖父节点为G,此时我们对上图中的a进行如下的颜色变化和旋转:
这样 就满足了红-黑树的颜色规则,树就成为了一棵平衡树,此时就能很容易地插入节点3,插入之后如上图中的b图所示。
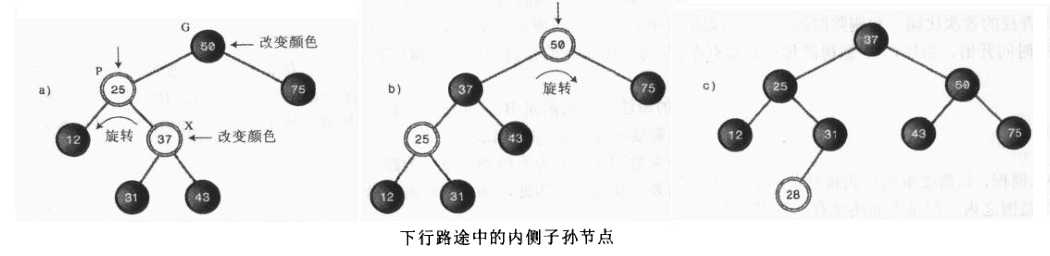
若插入的是内侧的子孙节点,此时我们以根为50,插入25,75,12,37,31和43.在插入12和31之前需要颜色变换,然后新插入节点28,向下查找插入点的时候,在37节点的时候需要执行颜色变换,变换后如下图的a树所示,变换后25和37都是红色需要进行旋转操作,此时颜色变换三角形的顶点X为37,P为25,G为50,执行以下四步使树从新平衡
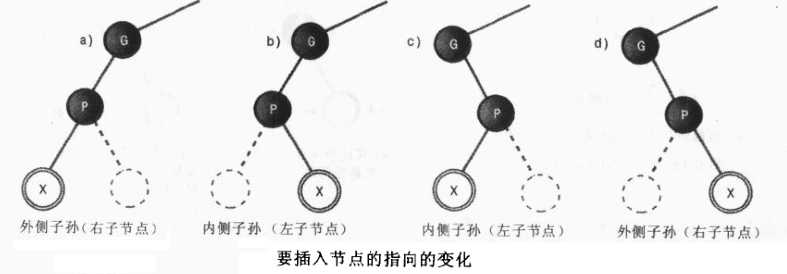
接下来我们讨论插入节点之后的旋转,这里我们讨论插入的节点为X,其父节点为P,祖父节点为G。1.若节点X在P的一侧与P在G的一侧相同,则X就是一个外侧的子孙节点(a,d),反之若不相同则X是一个内侧子孙节点(b,c)。下图显示了”指向“左右变化的多样性
为恢复红黑规则所执行的操作是由X和它的亲属所决定的,节点只以三种当时排列(上面的指向变换不算在内)
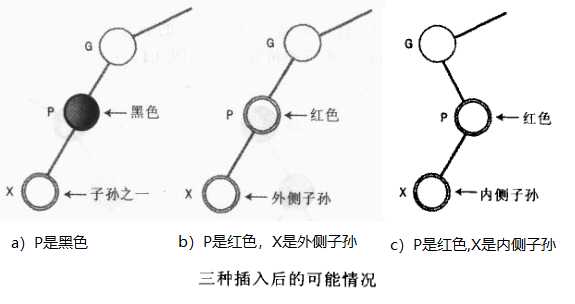
可能性1:若P是黑色的 :不需要做任何事情,由于插入的节点总是红色的。若父节点是黑色的,则 没有红色节点连接红色节点冲突也不会增加黑色节点数目,所以此时插入不需要做任何事情。
可能性2:P是红色,X是G的一个外侧子孙节点:这是插入后需要一次旋转和一些颜色变化,此时我们可以创建一个根为50的树,然后插入25,75和12。在插入12之前需要做一次颜色变换,然后向该树中插入6,得到下图中的a树,此时违背了红黑树规则,需要进行一下三个步骤的变换,
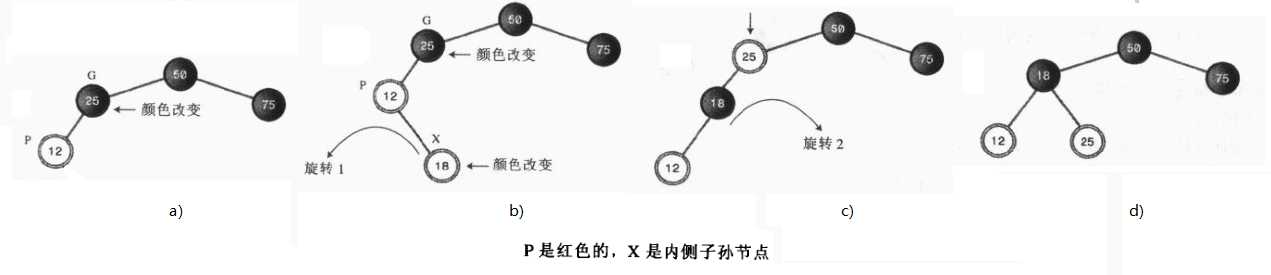
可能性3:P是红色的X是G的一个内侧的子孙节点,这时需要做两次旋转和一些颜色改变,首先我们创建一颗节点为50,25,75,12,18的树(在插入节点12之前需要一次颜色变换)插入12后的树如下图a所示,插入节点18是一个内侧子孙节点,他和他的父节点都是红色,首先第一次旋转将子孙节点变为外侧子孙节点,下图中的b->c然后就可以利用同情况1相同的旋转,颜色转换和旋转的步骤如下:
接下来我们讨论上面三种情况是否包含了所有的情况:
因此上面讨论的三种可能性是全部可能存在的情况(在可能性2和3中X可能是右子节点或者左子节点,以及G可能是右子节点或者左子节点)
之前我们讨论的二叉搜索树编写删除的代码比编写插入的操作的代码要难很多,红-黑树也是如此,删除节点后要恢复红黑规则变得很复杂,一般我们会用其他的方法来回避,比如说只将节点做删除的标记而不真正的删除
和一般的二叉搜索树类似,红-黑树的查找,插入删除的时间复杂度为O(log2N),红-黑树的查找时间和普通的二叉搜索树查找的时间几乎完全一样,额外的开销只是存储空间增加了一个存储红黑颜色的空间。
插入和删除的时间增加了一个常数因子,因为不得不在下行的路径上和插入点执行颜色变换和旋转。平均一次插入大概需要一次旋转,因此插入的时间复杂度还是O(log2N)但是比普通的二叉搜索树要慢(不用做颜色变换和旋转)
大多数应用中查找的次数比插入和删除的次数多,所以应用红-黑树取代二叉搜索树不会增加太多的时间开销,红黑树最大的优点就是对有序的数据的操作不会慢到O(N)的时间复杂度。
此篇就是关于红黑树结构的基本理解,不足之处欢迎指出,不懂得地方欢迎提问。
标签:img 技术分享 一个 相同 margin 代码 方向 介绍 str
原文地址:https://www.cnblogs.com/zhoukebo/p/9307685.html