标签:make 简单的 时间 状态 处理 增加 null class rand
同归并排序一样,快速排序也是将要排序的数组一分为二,但是与快速排序不同的是,归并排序不考虑任何条件直接将数组一分为二,之后再利用归并过程排序,而快速排序首先从将要排序的数组中选择一个元素,以这个元素为基准,如图所示
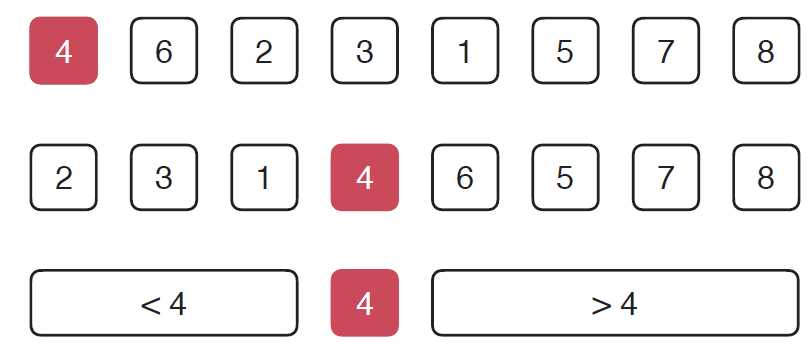
这里是选择的数组首元素4,然后把4挪到它在排好序的数组中应该在的位置, 这样,4之前的元素都比4小,4之后的元素都比4大。之后对两部分的子数组继续使用快速排序的思路进行排序,依次递归下去,直到排好序。那么,我们的关键任务就是如何把选择的基准元素(这里是首元素4)挪到正确的位置上,就是我们知道的partition方法。
《算法导论》中给出了选择数组首元素为基准元素的详细过程,这里,我们定义一些partition过程要使用到的变量,l是我们选择的基准元素v所在的位置,然后我们向右遍历我们的数组,将遍历过的元素分为两部分,小于v的元素部分和大于v的元素部分,这两部分的分界点,我们用j表示,而当前要考查的元素位置我们用i表示这样数组就变成了arr[l+1...j]<v 和 arr[j+1...i-1]>v 和待考察的部分,如何将要考查的元素划分到正确的集合(大于v还是小于v)呢

如果当前元素e大于v直接放入大于v的部分的后面一个位置即可,并同时将索引加1,数组就变成这样了 ,之后i++,考查下一个元素,如果,当前考查元素的e小于v,我们就需要把e放入橙色部分,我们首先想到的就是将两个位置交换,哪两个位置呢,因为j指向的是小于v的最后一个元素,肯定不能将j与i交换,交换的只能是j的下一个位置,它属于大于v的部分,交换之后,将i++,,就可以,直到所有元素都划分到正确的阵营,
,之后i++,考查下一个元素,如果,当前考查元素的e小于v,我们就需要把e放入橙色部分,我们首先想到的就是将两个位置交换,哪两个位置呢,因为j指向的是小于v的最后一个元素,肯定不能将j与i交换,交换的只能是j的下一个位置,它属于大于v的部分,交换之后,将i++,,就可以,直到所有元素都划分到正确的阵营,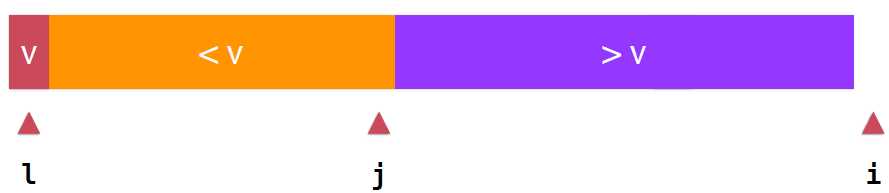 ,
,
v和arr[l+1...j]<v 以及 arr[j+1...i-1]>v ,然后将l位置和j位置交换即可,此时v就在正确的位置了,partition 代码如下
1 / partition the arr,the index j is the base element‘s position 2 // return an the integer j,make arr[l...j-1]<arr[j] and 3 // arr[j+1...r]>arr[j] 4 int partition(int arr[],int l,int r){ 5 int v = arr[l]; 6 int j = l; 7 for(int i = j+1;j<=r;j++){ 8 if(arr[j]<v){ 9 j++; 10 swap(arr[j],arr[i]); 11 } 12 } 13 swap(arr[j],arr[l]); 14 return j; 15 }
快速排序过程就是递归的调用partition过程
1 void __quick_sort(int arr[],int l,int r){ 2 while(l>=r) 3 return; 4 int p = partition(arr,l,r); 5 __quick_sort(arr,l,p-1); 6 __quick_sort(arr,p+1,r); 7 } 8 9 void qucik_sort(int arr[],int n){ 10 __quick_sort(arr,0,n-1); 11 }
不同于归并排序每次划分子数组的时候是对半划分,快速排序的partition操作将待排序的数组根据基准元素分成两部分,当数据有序性比较强的时候,那么分出的左右子数组规模就会不一样大,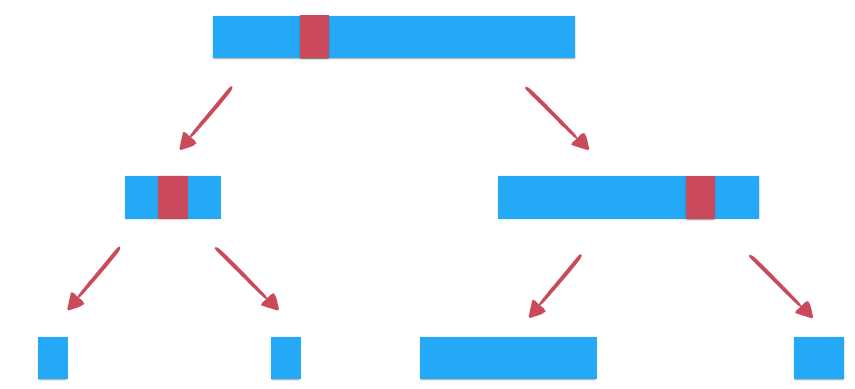 ,极端情况就是当数组完全有序的时候,就相当于一个链表了,这棵树的高度是N,这样总的时间复杂度就是O(N^2)级别的了,此时,我们可以选择选取基准元素的收获不是简单的选择数组首元素,而是希望选择大小处在中间的元素,这样这棵树就会相对平衡,但从算法处理上不是直接选择中间位置的元素,而是随机选择一个元素,从数学角度上可以证明这样的处理,快速排序的时间复杂度的期望是O(NlogN)的,我没有自己证明过,不过可以简单想一下,每一个被选择的概率都是1/N,我不执著于这个证明,我只是说一下,我认为这个期望是正确的。这样的处理只需要在原来方法上加上 swap(arr[rand()%(r-l+1)+l,arr[l]); 当然,当数据规模小的时候也可以像归并排序那样使用插入排序。
,极端情况就是当数组完全有序的时候,就相当于一个链表了,这棵树的高度是N,这样总的时间复杂度就是O(N^2)级别的了,此时,我们可以选择选取基准元素的收获不是简单的选择数组首元素,而是希望选择大小处在中间的元素,这样这棵树就会相对平衡,但从算法处理上不是直接选择中间位置的元素,而是随机选择一个元素,从数学角度上可以证明这样的处理,快速排序的时间复杂度的期望是O(NlogN)的,我没有自己证明过,不过可以简单想一下,每一个被选择的概率都是1/N,我不执著于这个证明,我只是说一下,我认为这个期望是正确的。这样的处理只需要在原来方法上加上 swap(arr[rand()%(r-l+1)+l,arr[l]); 当然,当数据规模小的时候也可以像归并排序那样使用插入排序。
下面我们重点要说的是另一种优化方法,是通过划分方式的不同,就是partition方式的不同的优化。前面提到,引起退化是原因是数组的有序性强,从而树的不平衡使树的高度不再是log(N)的了,所以可以考虑partition的方式使得划分的树尽量平衡。回顾一下,上面的partition操作,如果当前考查元素小于v,就划分到橙色小于v的部分,也就是对于大于等于v的元素都划分到紫色的部分了,这就会造成树 的不平衡,如果,我们能让等于v的元素尽量平均的分布在两个部分,那这棵树就平衡了。如图所示
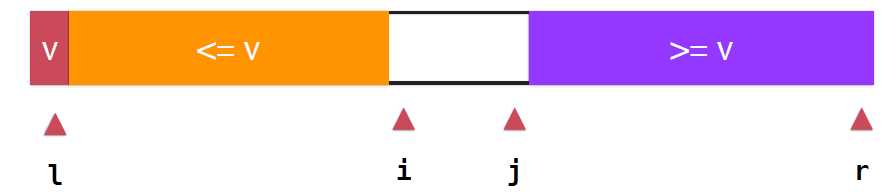
那么久应该再增加一个索引跟踪大于v这部分下一个要考查的元素的位置,假如现在的状态就如上图所示,继续扫描,i++,当这个元素小于v的时候,继续向后扫描直到碰到了某个元素e大于等于v停止扫描,同样,右端从J向前扫描,如果是大于v,继续向前,直到遇到e是小于等于v的元素,停止扫描,整个关系如下图
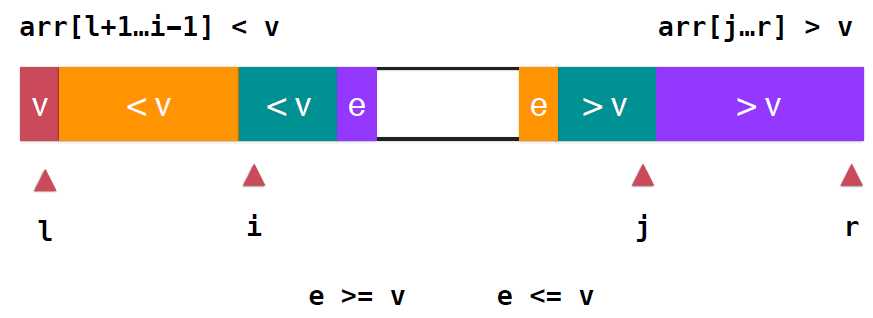
对于小于和大于的两端的深绿色部分应分别并入橙色和紫色的部分,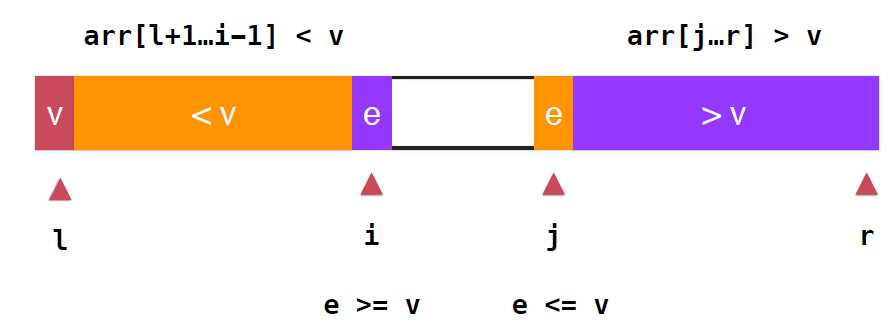 ,对于i,j两个位置交换位置即可,此时橙色部分都是小于v的元素,紫色部分都是大于v的元素,继续扫描,i向后,j向前,直到i,j重合,数组遍历完毕,不过,这里需要注意,实际上橙色部分是小于等于v的,紫色部分是大于等于v的,
,对于i,j两个位置交换位置即可,此时橙色部分都是小于v的元素,紫色部分都是大于v的元素,继续扫描,i向后,j向前,直到i,j重合,数组遍历完毕,不过,这里需要注意,实际上橙色部分是小于等于v的,紫色部分是大于等于v的,
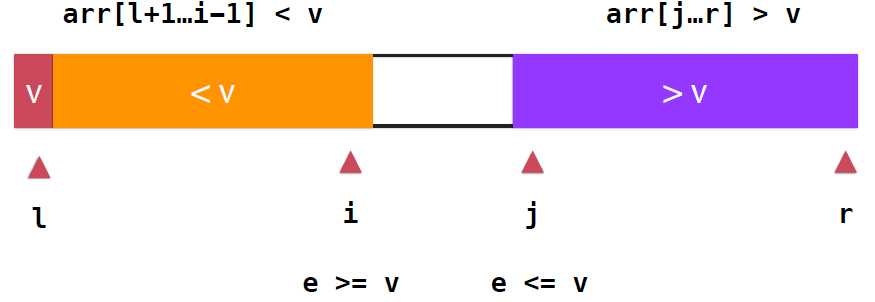
partition实现如下:
1 //return j, make arr[l...j-1] <arr[j],arr[j+1...r]?arr[j] 2 int partition2(int arr[],int l,int r){ 3 swap(arr[rand()%(r-l+1)+l,arr[l]]); 4 int v = arr[l]; 5 int i = l+1,j = r; 6 while(true){ 7 while(arr[i]<v && i<=r) 8 i++; 9 while(arr[j]>v && j>l) 10 j--; 11 if(i>j) 12 break; 13 swap(arr[i],arr[j]); 14 i++; 15 j--; 16 } 17 swap(arr[l],arr[j]); 18 return j; 19 }
Optimization 2 三路快速排序
根据名称就很容易想到三路快速排序的思想,之前,都是将整个数组分成两部分,等于v的部分和小于v的部分,显然,三路快速排序就是将整个数组分成三部分,大于v,等于v,小于v,如下图所示。其中lt指向小于v的最后一个元素,gt指向了第一个大于v的的元素,i依然是指向当前要考查的元素,这样就满足如下 arr[l+1...lt]>v; arr[gt...r]>v; arr[lt+1...i-1]==v ,然后就是如何处理当前要考查的arr[i],
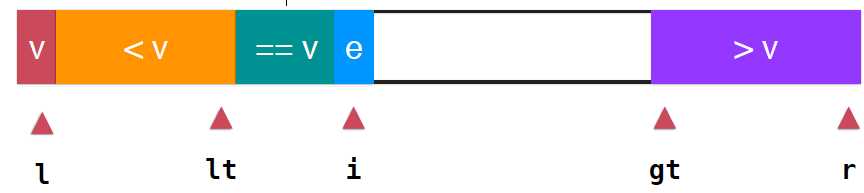
当e==v: i++,e直接并入深绿色的等于v的部分,接着考查下一个元素,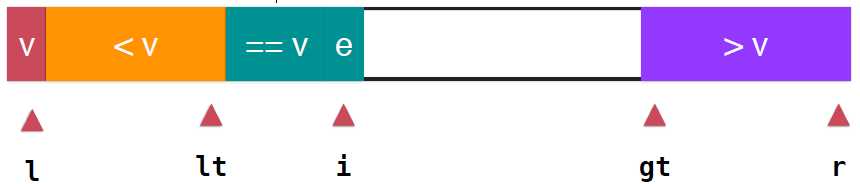
当e<v:同之前处理两路快速排序同样的操作,只需要将e与等于v部分的第一个元素交换位置即可,然后lt++,即可,i++继续考查下一个元素
当e>v时,相似的操作,只需要将v与gt前面的元素交换,然后gt--,此时e就是大于v部分的第一个元素,因为此时i指向的元素是原来gt-1指向的,还未考查,所以,此时不用跟新i
最后,所有元素考查完成后应该是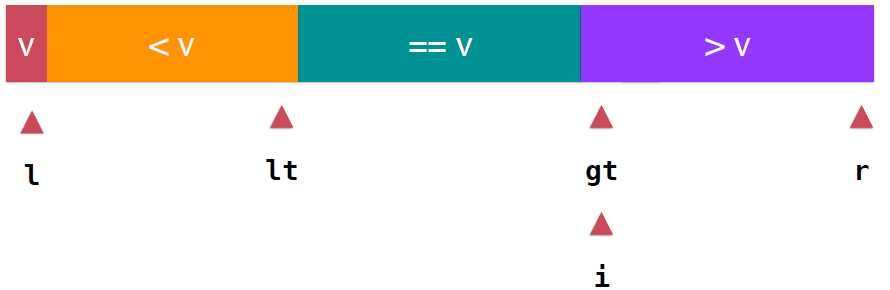 ,整个数组分成了<v,大于v,等于v三部分,lt指向了<v部分的最后一个元素,gt指向大于v部分的第一个元素,此时,i的位置就是gt的位置。显然,我们只需要将v与lt指向的元素交换,v就处在了正确的位置上,如下图。
,整个数组分成了<v,大于v,等于v三部分,lt指向了<v部分的最后一个元素,gt指向大于v部分的第一个元素,此时,i的位置就是gt的位置。显然,我们只需要将v与lt指向的元素交换,v就处在了正确的位置上,如下图。
 ,之后就是小于v 的部分和小于v的部分递归的partition操作,对于等于v的部分已经处在了正确的位置了。很明显,它的优势就是不需要对重复元素递归的partition操作,从而提高了效率。
,之后就是小于v 的部分和小于v的部分递归的partition操作,对于等于v的部分已经处在了正确的位置了。很明显,它的优势就是不需要对重复元素递归的partition操作,从而提高了效率。
由于三路快拍不是简单的返回一个索引j,然后对arr[l...j-1],arr[j+1...r]进行递归就好了,因为中间等于v的部分是一个集合(一段区间),不再是一个元素,不好再设计一个partition函数了,方便返回了,我们直接在quick_sort 中实现partition操作。实现如下
//three ways quick sort for arr //divide the arr[l...r] to three parts <v,==v,>v //recursion the <v-part and >v-part __quick_sort3Ways(int arr[],int l,int r){ if(r-l<15) insertion_sort(arr,l,r); //partition swap(arr[rand()%(r-l+1)+l],arr[l]); int v = arr[l]; int lt = l+1; // arr[l...lt]<v int gt = r+1; //arr[gt...r]>v int i = l+1; // arr[lt+1...i)==v while(i<gt){ if(arr[i]<v){ swap(arr[i],arr[lt+1]); lt++; i++; } else if(arr[i]>v){ swap(arr[gt-1],arr[i]); gt--; } else i++; } swap(arr[l],arr[lt]); __quick_sort3Ways(arr,l,lt-1); __quick_sort3Ways(arr,gt,r); } qucik_sort3Ways(int arr[],int n){ srand(time(NULL)); __quick_sort3Ways(arr,0,n-1); }
归并排序和快速排序都用到了分治(divide-and-conquer)算法的思想,顾名思义,分而治之,就是将原问题分解为相同结构的子问题,然后,逐一解决子问题的思想方法。归并排序和快速排序都是将原问题分解为两个子问题。不同的是,归并排序没有任何考虑直接将原问题一分为二,然后递归的归并排序,关键是,分完后,如何再归并起来,对于快速排序的关键点是如何分,我们的做法是选择一个参照元素,以参照元素为届划分,最后再将参照元素移动到正确的位置上。这样的分,我们就不用考虑合的问题,只需递归执行就可以了。
标签:make 简单的 时间 状态 处理 增加 null class rand
原文地址:https://www.cnblogs.com/Holly-blog/p/9312031.html