The Multilinear Structure of ReLU Networks

标签：com   spl   ted   img   分享图片   cells   sub   ext   一个   

两种非常常见的非线性单元：rectified linear units (ReLUs) 和 leaky ReLUs

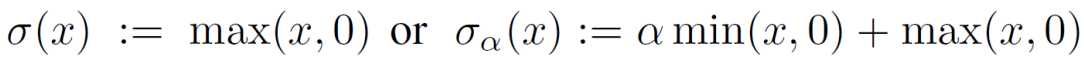
我们选取binary hinge loss进行二分类

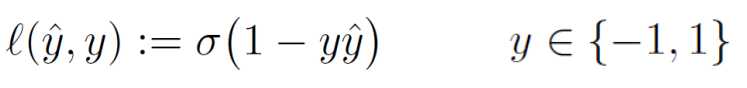
对于多分类，我们可以定义multiclass hinge loss

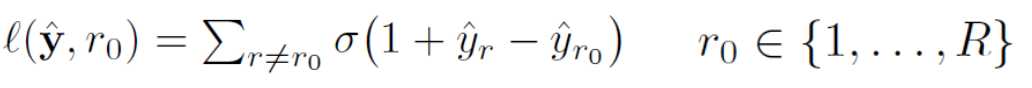
定义Ω为网络的参数空间， L(ω)为loss。

由于我们选了ReLU非线性单元作为loss, 那么L(ω)是分片线性的。对于参数空间，我们可以将其进行一个划分，

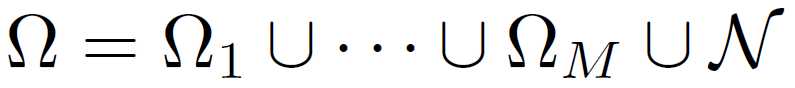
分成有限个open cells Ω_u 和 边界N，则损失函数L(ω)在cell的内部是光滑的，在边界上是不可微的。

下面我们将loss限制在某个cell  Ω_u上单独考虑，并且loss拥有multilinear form. 由于multilinear form是调和的，由strong maximum principle知，极值点必定在边界处N. 换句话说，ReLU 神经网络 with hinge loss L(ω)是不存在可微的局部极值点的。

目前为止，我们可以知道局部极值有两种情况，

Type I (Flat). 局部极值在cell中，loss为常值。

Type II (Sharp). 局部极值在边界N上。

Main Result 1.   在Type II局部极值点，L(ω)>0.

也就是说，如果存在极值0，那么Type II极值点都是sub-optimal的。

若我们考虑更一般的情况：fully connected networks with leaky ReLU nonlinearities. 那么我们有以下结果，

Main Result 2.  在Type I局部极值点，L(ω)=0. 在Type II局部极值点，L(ω)>0.

在存在极值0的情况下，flat 局部极小值都是optimal的，sharp 局部极小值都是sub-optimal的。若不存在极值0，所有的局部极值点都是sharp的。

未完待续。。。

The Multilinear Structure of ReLU Networks

标签：com   spl   ted   img   分享图片   cells   sub   ext   一个   

原文地址：https://www.cnblogs.com/skykill/p/9338233.html