标签:src tor image 添加 并且 c++ oid 容量 span
前面提到过,可以考虑倍增,这里就以容器vector的倍增为例,这也是《C++ primer》中提到过的倍增,并且测试了下时间,主要是验证时间时间复杂度问题
每次添加一个元素的时间复杂度是O(1),添加到n(假设初始容量是n)个元素的时候,需要倍增扩容同时将原来的数据拷贝到现在的新的数组中,那么前面n次添加总的时间复杂度是O(n),拷贝操作的复杂度是O(n),总的就是O(2n),平均每场操作就是O(2),
删除元素(pop操作)的时候,也会想到删到capacity的1/2的时候,resize操作,看着没什么问题,但是,如果恰好pop到capacity的1/2的时候,即临界点的时候pop,push不停的交替进行,那么这时候时间复杂度就退化到O(n),了所以,为例避免这种情况出现,扩容操作和缩减操作的度量不同,当pop到capacity的1/4的时候,再resize操作,只是resize到的仍是capacity的1/2。
vector的件件框架如下:
1 template<typename T> 2 class MyVector{ 3 private: 4 T* data; 5 int size; 6 int capacity; 7 private: 8 void resize(int newCapacity){ 9 assert(newCapacity>=size); 10 T* newData = new T[newCapacity]; 11 for(int i = 0;i<=size;i++) 12 newData[i] = data[i]; 13 delete[] data; 14 data = newData; 15 capacity = newCapacity; 16 } 17 public: 18 MyVector(){ 19 data = new T[100]; 20 capacity =100; 21 size =0; 22 } 23 ~MyVector(){ 24 delete[] data; 25 } 26 void push_back(T e){ 27 if(size == capacity) 28 resize(2*capacity); 29 data[size++] = e; 30 } 31 32 T pop_back(){ 33 assert(size>0); 34 T e = data[size-1]; 35 size--; 36 if(size == capacity/4) 37 resize(capacity/2); 38 return e; 39 } 40 };
测试如下:
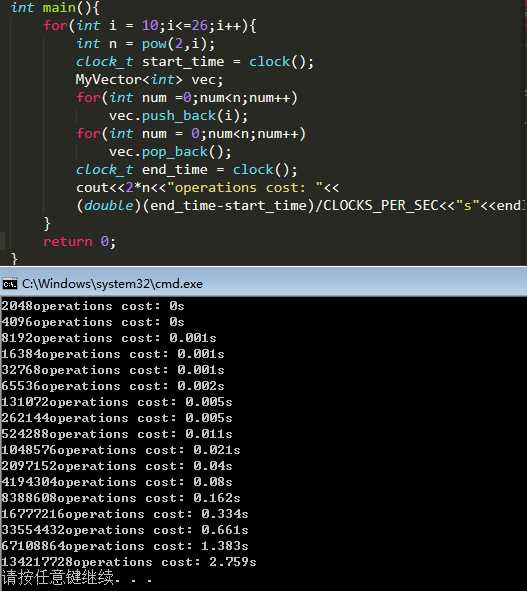
标签:src tor image 添加 并且 c++ oid 容量 span
原文地址:https://www.cnblogs.com/Holly-blog/p/9343445.html