内部排序->选择排序->树形选择排序

时间：2018-07-26 21:12:31 阅读：228 评论：0 收藏：0 [点我收藏+]

文字描述

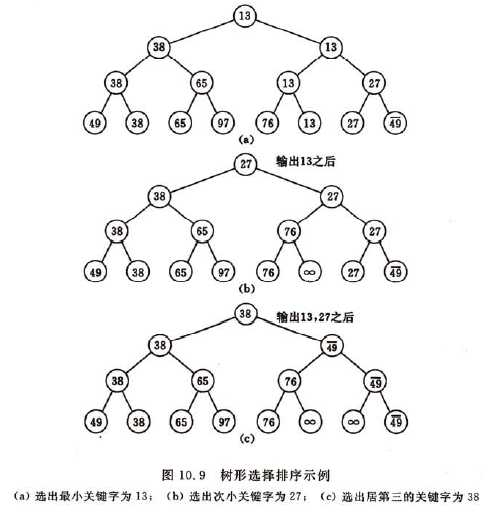
　　树形选择排序又称锦标赛排序; 比如,在8个运动员中决出前3名至多需要11场比赛, 而不是7+6+5=18场比赛(它的前提是甲胜乙，乙胜丙，则甲必能胜丙)

　　首先对n个记录的关键字进行两两比较，然后在(n/2)个较小者之间再进行两两比较，直至选出最小关键字的记录为止，这个过程可用一颗有n个叶子结点的完全二叉树表示。关于完全二叉树的定义和与本排序算法用到的性质见附录1

示意图

算法分析

　　由于含n个叶子结点的完全二叉树的深度为[log2n]+1, 则在树形选择排序中，除了最小关键字外，每选择一个次小关键字仅需进行log2n次比较，因此它的时间复杂度为nlogn.。但是它需要的辅助空间为2*n-1。而且它在选择过程中，和"最大值"进行了多余的比较。另外，该算法是不稳定的。

代码实现

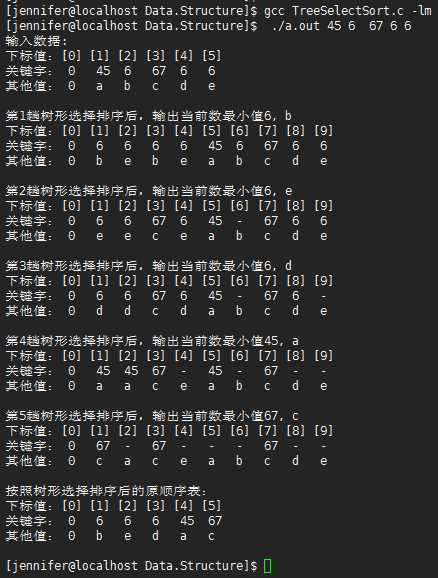
  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 #include <math.h>
  4 /*
  5  * double log2(double x);    以2为底的对数
  6  * double ceil(double x);    取上整
  7  * double floor(double x);    取下整
  8  * double fabs(double x);    取绝对值
  9  */
 10 
 11 #define DEBUG
 12 
 13 #define EQ(a, b) ((a) == (b))
 14 #define LT(a, b) ((a) <  (b))
 15 #define LQ(a, b) ((a) <= (b))
 16 
 17 #define MAXSIZE  100
 18 #define INF         1000000
 19 typedef int KeyType;
 20 typedef char InfoType;
 21 typedef struct{
 22     KeyType key;
 23     InfoType otherinfo;
 24 }RedType;
 25 
 26 typedef struct{
 27     RedType r[MAXSIZE+1];
 28     int length;
 29 }SqList;
 30 
 31 void PrintList(SqList L){
 32     int i = 0;
 33     printf("下标值：");
 34     for(i=0; i<=L.length; i++){
 35         printf("[%d] ", i);
 36     }
 37     printf("\n关键字：");
 38     for(i=0; i<=L.length; i++){
 39         if(EQ(L.r[i].key, INF)){
 40             printf(" %-3c", ‘-‘);
 41         }else{
 42             printf(" %-3d", L.r[i].key);
 43         }
 44     }
 45     printf("\n其他值：");
 46     for(i=0; i<=L.length; i++){
 47         printf(" %-3c", L.r[i].otherinfo);
 48     }
 49     printf("\n\n");
 50     return ;
 51 }
 52 
 53 /*树形选择排序算法*/
 54 void TreeSelectSort(SqList *L)
 55 {
 56     //为实现该排序所需的辅助树
 57     SqList tree;
 58     //辅助树的大小
 59     tree.length = L->length-1 + L->length;
 60 
 61     tree.r[0].otherinfo = ‘0‘;
 62     int i = 0, low = 1;
 63     //由后向前填充此树的叶子结点
 64     for(i=0; i<L->length; i++){
 65         tree.r[tree.length-i] = L->r[L->length-i];
 66     }
 67     //由后向前填充此树的非叶子结点
 68     for(i=(tree.length-L->length); i>=1; i--){
 69         tree.r[i] = (LT(tree.r[2*i].key, tree.r[2*i+1].key)?tree.r[2*i]:tree.r[2*i+1]);
 70     }
 71     //纪录当前辅助树的最小结点
 72     RedType minred;
 73     //记录最小结点在叶子结点中的下标值
 74     int minindex = 0;
 75     while(low <= L->length){
 76         minred = tree.r[1];
 77 #ifdef DEBUG
 78         printf("第%d趟树形选择排序后，输出当前数最小值%d, %c\n", low, minred.key, minred.otherinfo);
 79         PrintList(tree);
 80 #endif
 81         //不断移走最小结点
 82         L->r[low++] = minred;
 83         minindex = tree.length;
 84         //找到最小值在辅助树叶子结点中的下标值
 85         for(minindex=tree.length; (minindex>(tree.length-L->length)); minindex--){
 86             if(EQ(tree.r[minindex].key, minred.key) && EQ(tree.r[minindex].otherinfo, minred.otherinfo)){
 87                 break;
 88             }
 89         }
 90         //设置一个最大值标志，INF表示无穷大
 91         tree.r[minindex].key = INF;
 92         //重新调整此辅助树，使根结点关键字值最小
 93         for(i=(minindex/2); i>=1; i/=2){
 94             tree.r[i] = (LT(tree.r[2*i].key, tree.r[2*i+1].key)?tree.r[2*i]:tree.r[2*i+1]);
 95         }
 96     }
 97 #ifdef DEBUG
 98     printf("按照树形选择排序后的原顺序表：\n");
 99     PrintList(*L);
100 #endif
101 }
102 
103 int  main(int argc, char *argv[])
104 {
105     if(argc < 2){
106         return -1;
107     }
108     SqList L;
109     int i = 0;
110     for(i=1; i<argc; i++){
111         if(i>MAXSIZE)
112             break;
113         L.r[i].key = atoi(argv[i]);
114         L.r[i].otherinfo = ‘a‘+i-1;
115     }
116     L.length = (i-1);
117     L.r[0].key = 0;
118     L.r[0].otherinfo = ‘0‘;
119     printf("输入数据:\n");
120     PrintList(L);
121     //对顺序表L作树形选择排序
122     TreeSelectSort(&L);
123     return 0;
124 }