标签:图片 mod 利用 esc order 最大值 show 区别 最简
一、感知机介绍
感知器(英语:Perceptron)是Frank Rosenblatt在1957年就职于康奈尔航空实验室(Cornell Aeronautical Laboratory)时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。Frank Rosenblatt给出了相应的感知机学习算法,常用的有感知机学习、最小二乘法和梯度下降法。譬如,感知机利用梯度下降法对损失函数进行极小化,求出可将训练数据进行线性划分的分离超平面,从而求得感知机模型。感知机是生物神经细胞的简单抽象。神经细胞结构大致可分为:树突、突触、细胞体及轴突。单个神经细胞可被视为一种只有两种状态的机器——激动时为‘是’,而未激动时为‘否’。神经细胞的状态取决于从其它的神经细胞收到的输入信号量,及突触的强度(抑制或加强)。当信号量总和超过了某个阈值时,细胞体就会激动,产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。为了模拟神经细胞行为,与之对应的感知机基础概念被提出,如权量(突触)、偏置(阈值)及激活函数(细胞体)。
在人工神经网络领域中,感知机也被指为单层的人工神经网络,以区别于较复杂的多层感知机(Multilayer Perceptron)。作为一种线性分类器,(单层)感知机可说是最简单的前向人工神经网络形式。尽管结构简单,感知机能够学习并解决相当复杂的问题。感知机主要的本质缺陷是它不能处理线性不可分问题。
二、感知机原理
感知机算法的原理和线性回归算法的步骤大致相同,只是预测函数H和权值更新规则不同,这里将感知机算法应用于二分类。
三、数据集介绍
乳腺癌数据集,其实例数量是569,实例中包括诊断类和属性,帮助预测的属性是30,各属性包括为radius 半径(从中心到边缘上点的距离的平均值),texture 纹理(灰度值的标准偏差)等等,类包括:WDBC-Malignant 恶性和WDBC-Benign 良性。用数据集的70%作为训练集,数据集的30%作为测试集,训练集和测试集中都包括特征和诊断类。
四、感知机算法的代码实现与结果分析
代码实现:
import pandas as pd#用pandas读取数据
import matplotlib.pyplot as plt
import numpy as np
from sklearn import preprocessing
from matplotlib.colors import ListedColormap
from perceptron import Perceptron
from scipy.special import expit#这是sign()函数
from sklearn.model_selection import train_test_split
def loadDataSet():
# df=pd.read_csv("Breast_ Cancer_ Data.csv")
# # print(df.head())
# # print(df.tail())
# label=df.ix[:,1]
# data=df.ix[:,2:32]#数据类型没有转换,比如31.48,是str类型,需要将其转换为float
#
# m=data.shape[0]
# data=np.array(data,dtype=float)
#
# for i in range(m):
# if label[i]==‘B‘:
# label[i]=0
# else :
# label[i]=1
# train_x, test_x, train_y, test_y = train_test_split(data, label, test_size=0.30, random_state=0) # 划分数据集和测试集
df = pd.read_csv("Breast_ Cancer_ Data.csv")
dataArray=np.array(df)
testRatio=0.3
dataSize=dataArray.shape[0]
testNum=int(testRatio*dataSize)
trainNum=dataSize-testNum
train_x=np.array(dataArray[0:trainNum,2:],dtype=np.float)
test_x=np.array(dataArray[trainNum:,2:],dtype=np.float)
train_y=dataArray[0:trainNum,1]
test_y = dataArray[trainNum:, 1]
for i in range(trainNum):
if train_y[i]==‘B‘:
train_y[i]=1
else:
train_y[i]=0
for i in range(testNum):
if test_y[i] == ‘B‘:
test_y[i] = 1
else:
test_y[i] = 0
return train_x,test_x,train_y,test_y
# def sign(inner_product):
# if inner_product >= 0:
# return 1
# else:
# return 0
#学习模型,学的参数theta
def train_model(train_x,train_y,theta,learning_rate,iteration):
m=train_x.shape[0]
n=train_x.shape[1]
J_theta=np.zeros((iteration,1))#列向量
train_x=np.insert(train_x,0,values=1,axis=1)#相当于x0,加在第一列上
for i in range(iteration):#迭代
# temp=theta #暂存
# J_theta[i]=sum(sum((train_y-expit(np.dot(train_x,theta)))**2)/2.0)#dot是内积,sum函数是将减掉后的列向量求和成一个数
J_theta[i]=sum((train_y[:,np.newaxis]-expit(np.dot(train_x,theta)))**2)/2.0#dot是内积,sum函数是将减掉后的列向量求和成一个数
for j in range(n):#j是第j个属性,但是所有属性对应的的theta都要更新,故要循环
# temp[j]=temp[j]+learning_rate*np.dot((train_x[:,j].T)[np.newaxis],(train_y[:,np.newaxis]-expit(np.dot(train_x,theta))))#T是转置
# temp[j]=temp[j]+learning_rate*np.dot(train_x[:,j].T,(train_y-expit(np.dot(train_x,theta))))#T是转置
theta[j]=theta[j]+learning_rate*np.dot((train_x[:,j].T)[np.newaxis],(train_y[:,np.newaxis]-expit(np.dot(train_x,theta))))#T是转置
# theta=temp
x_iteration=np.linspace(0,iteration,num=iteration)
plt.plot(x_iteration,J_theta)
plt.show()
return theta
def predict(test_x,test_y,theta):#假设theta是已经学习好的参数传递进来
errorCount=0
m=test_x.shape[0]
test_x=np.insert(test_x,0,values=1,axis=1)#相当于x0
h_theta = expit(np.dot(test_x, theta))
for i in range(m):
if h_theta[i]>0.5:
h_theta[i]=1
else:
h_theta[i]=0
if h_theta[i]!=test_y[i]:#test_y[i]需要是0或者1才能比较,因为h_theta[i]就是0或者1
errorCount+=1
error_rate=float(errorCount)/m
print("error_rate ",error_rate)
#特征缩放中的标准化方法,注意:numpy中的矩阵运算要多运用
def Standardization(x):#x是data
m=x.shape[0]
n=x.shape[1]
x_average=np.zeros((1,n))#x_average是1*n矩阵
sigma = np.zeros((1, n)) # sigma是1*n矩阵
x_result=np.zeros((m, n)) # x_result是m*n矩阵
x_average=sum(x)/m
# x_average = x.mean(axis=0)#用np的mean函数也可以求得每一列的平均值
# for i in range(n):
# for j in range(m):
# x_average[0][i] +=(float(x[j][i]))
# x_average[0][i]/=m
# sigma=(sum((x-x_average)**2)/m)**0.5#m*n的矩阵减去1*n的矩阵的话,会广播,1*n的矩阵会复制成m*n的矩阵
sigma = x.var(axis=0) # 用np的var函数来求每一列的方差
# for i in range(n):
# for j in range(m):
# sigma[0][i]+=((x[j][i]-x_average[0][i])**2.0)
# sigma[0][i]=(sigma[0][i]/m)**0.5
x_result=(x-x_average)/sigma#对应的元素相除
# for i in range(n):
# for j in range(m):
# x_result[j][i]=(x[j][i]-x_average[0][i])/sigma[0][i]
return x_result
#特征缩放中的调节比例方法
def Rescaling(x):
m = x.shape[0]
n = x.shape[1]
x_min=np.zeros((1,n))#x_min是1*n矩阵
x_max=np.zeros((1,n))#x_max是1*n矩阵
x_result = np.zeros((m, n)) # x_result是m*n矩阵
# for i in range(n):
# x_min[0][i]=x[0][i]
# x_max[0][i]=x[0][i]
# for j in range(1,m):
# if x_min[0][i]>x[j][i]:
# x_min[0][i]=x[j][i]
# if x_max[0][i]<x[j][i]:
# x_max[0][i]=x[j][i]
# for i in range(n):
# for j in range(m):
# x_result[j][i]=(x[j][i]-x_min[0][i])/(x_max[0][i]-x_min[0][i])
x_min=x.min(axis=0)#获得每个列的最小值
x_max=x.max(axis=0)#获得每个列的最大值
x_result = (x - x_min) / (x_max - x_min)
return x_result
if __name__==‘__main__‘:
train_x, test_x, train_y, test_y=loadDataSet()
# scaler=preprocessing.MinMaxScaler()
# train_x=scaler.fit_transform(train_x)
# test_x=scaler.fit_transform(test_x)
# train_x=Standardization(train_x)
# test_x=Standardization(test_x)
# train_x=Rescaling(train_x)
# test_x=Rescaling(test_x)
n=test_x.shape[1]+1
theta=np.zeros((n,1))
# theta=np.random.rand(n,1)#随机构造1*n的矩阵
theta_new=train_model(train_x,train_y,theta,learning_rate=0.001,iteration=1000)#用rescaling的时候错误率0.017
predict(test_x, test_y, theta_new)
结果展示和分析:
感知机分类乳腺癌数据集的实验
实验的迭代次数1000,学习率0.001,对特征缩放的方法效果进行比较,如表3所示。
表3 分类错误率和特征缩放的方法的关系
|
特征缩放 |
Standardization |
Rescaling |
|
分类错误率 |
0.182 |
0.017 |
Standardization标准化方法的J随着迭代次数的变化图如图1所示:
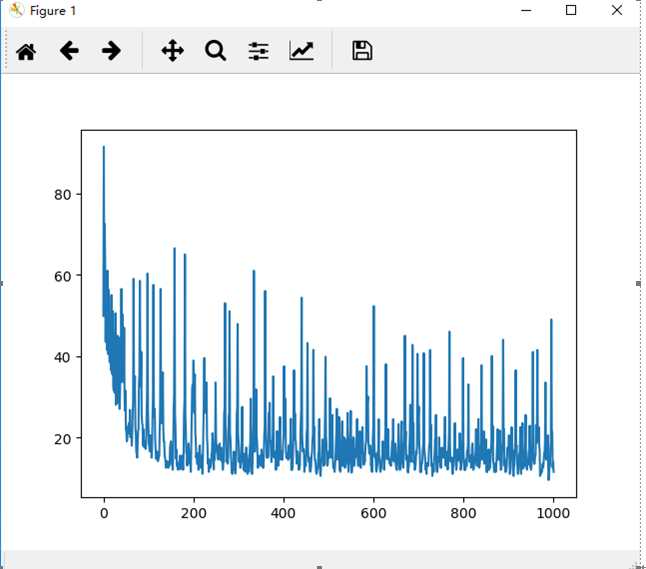
图1 标准化方法的效果图
Rescaling调节比例方法的J随着迭代次数的变化图如图2所示:
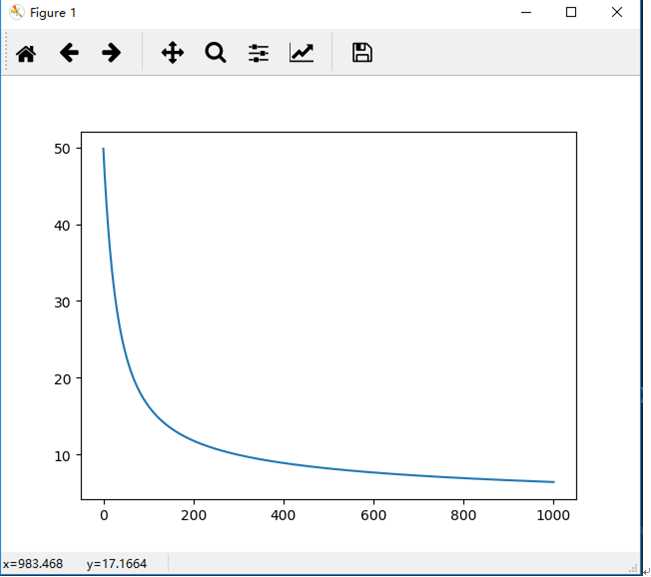
图2 调节比例方法的效果图
图1 说明迭代次数和学习率等参数未调节到使效果较好的值;图2的效果比较好,损失函数逐渐降低并且趋于平缓;比较两种方法,相对来说调节比例的方法优于标准化方法。
标签:图片 mod 利用 esc order 最大值 show 区别 最简
原文地址:https://www.cnblogs.com/BlueBlue-Sky/p/9383097.html