标签:job 中间 文档 from else 优化器 排列 ntile 新版
上篇文字,我们知道如何获取数据了,那现在就把它们联接起来!
我要展现的是3个个常用联接运算符:合并联接(Merge join),哈希联接(Hash Join)和嵌套循环联接(Nested Loop Join)。但是在此之前,我需要引入新词汇了:内关系和外关系(inner relation and outer relation)。
一个关系可以是:
一个表
一个索引
上一个运算的中间结果(比如上一个联接运算的结果)。
当你联接两个关系时,联接算法对两个关系的处理是不同的。在本文剩余部分,我将假定:
外关系是左侧数据集
内关系是右侧数据集
比如, A JOIN B 是 A 和 B 的联接,这里 A 是外关系,B 是内关系。
多数情况下,A JOIN B 的成本跟 B JOIN A 的成本是不同的。
在这一部分,我还将假定外关系有 N 个元素,内关系有 M 个元素。要记住,真实的优化器通过统计知道 N 和 M 的值。
注:N 和 M 是关系的基数。【注:基数】
嵌套循环联接是最简单的。
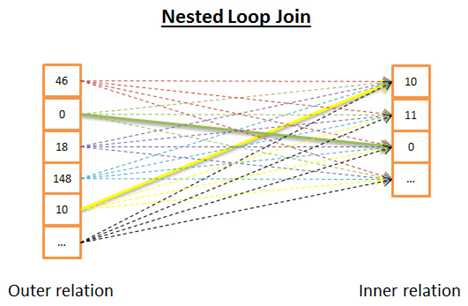
道理如下:
1 针对外关系的每一行
2 查看内关系里的所有行来寻找匹配的行
下面是伪代码:
nested_loop_join(array outer,array inner) foreach row a in outer foreach row b in inner if(match_join_condition(a,b)) write_result_in_output(a,b) end if end for end for
由于这是个双迭代,时间复杂度是 O(N*M)。
在磁盘 I/O 方面, 针对 N 行外关系的每一行,内部循环需要从内关系读取 M 行。这个算法需要从磁盘读取 N+ N*M 行。但是,如果内关系足够小,你可以把它读入内存,那么就只剩下 M + N 次读取。这样修改之后,内关系必须是最小的,因为它有更大机会装入内存。
在CPU成本方面没有什么区别,但是在磁盘 I/O 方面,最好最好的,是每个关系只读取一次。
当然,内关系可以由索引代替,对磁盘 I/O 更有利。
由于这个算法非常简单,下面这个版本在内关系太大无法装入内存时,对磁盘 I/O 更加有利。道理如下:
1 为了避免逐行读取两个关系,
2 你可以成簇读取,把(两个关系里读到的)两簇数据行保存在内存里,
3 比较两簇数据,保留匹配的,
4 然后从磁盘加载新的数据簇来继续比较
5 直到加载了所有数据。
可能的算法如下:
// improved version to reduce the disk I/O. nested_loop_join_v2(file outer, file inner) for each bunch ba in outer // ba is now in memory for each bunch bb in inner // bb is now in memory for each row a in ba for each row b in bb if (match_join_condition(a,b)) write_result_in_output(a,b) end if end for end for end for end for
使用这个版本,时间复杂度没有变化,但是磁盘访问降低了:
用前一个版本,算法需要 N + N*M 次访问(每次访问读取一行)。
用新版本,磁盘访问变为外关系的数据簇数量 + 外关系的数据簇数量 * 内关系的数据簇数量。
增加数据簇的尺寸,可以降低磁盘访问。
哈希联接更复杂,不过在很多场合比嵌套循环联接成本低。
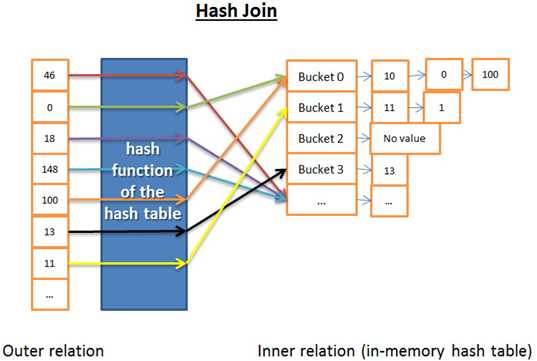
哈希联接的道理是:
1) 读取内关系的所有元素
2) 在内存里建一个哈希表
3) 逐条读取外关系的所有元素
4) (用哈希表的哈希函数)计算每个元素的哈希值,来查找内关系里相关的哈希桶内
5) 是否与外关系的元素匹配。
在时间复杂度方面我需要做些假设来简化问题:
1 内关系被划分成 X 个哈希桶
2 哈希函数几乎均匀地分布每个关系内数据的哈希值,就是说哈希桶大小一致。
3 外关系的元素与哈希桶内的所有元素的匹配,成本是哈希桶内元素的数量。
时间复杂度是 (M/X) * N + 创建哈希表的成本(M) + 哈希函数的成本 * N 。
如果哈希函数创建了足够小规模的哈希桶,那么复杂度就是 O(M+N)。
还有个哈希联接的版本,对内存有利但是对磁盘 I/O 不够有利。 这回是这样的:
1) 计算内关系和外关系双方的哈希表
2) 保存哈希表到磁盘
3) 然后逐个哈希桶比较(其中一个读入内存,另一个逐行读取)。
合并联接是唯一产生排序的联接算法。
注:这个简化的合并联接不区分内表或外表;两个表扮演同样的角色。但是真实的实现方式是不同的,比如当处理重复值时。
1.(可选)排序联接运算:两个输入源都按照联接关键字排序。
2.合并联接运算:排序后的输入源合并到一起。
排序
我们已经谈到过合并排序,在这里合并排序是个很好的算法(但是并非最好的,如果内存足够用的话,还是哈希联接更好)。
然而有时数据集已经排序了,比如:
1 如果表内部就是有序的,比如联接条件里一个索引组织表【index-organized table】
2 如果关系是联接条件里的一个索引
3 如果联接应用在一个查询中已经排序的中间结果
合并联接
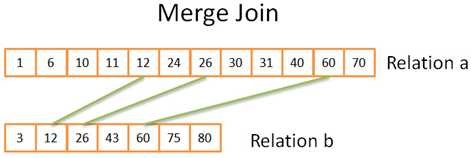
这部分与我们研究过的合并排序中的合并运算非常相似。不过这一次呢,我们不是从两个关系里挑选所有元素,而是只挑选相同的元素。道理如下:
1) 在两个关系中,比较当前元素(当前=头一次出现的第一个)
2) 如果相同,就把两个元素都放入结果,再比较两个关系里的下一个元素
3) 如果不同,就去带有最小元素的关系里找下一个元素(因为下一个元素可能会匹配)
4) 重复 1、2、3步骤直到其中一个关系的最后一个元素。
因为两个关系都是已排序的,你不需要『回头去找』,所以这个方法是有效的。
该算法是个简化版,因为它没有处理两个序列中相同数据出现多次的情况(即多重匹配)。真实版本『仅仅』针对本例就更加复杂,所以我才选择简化版。
如果两个关系都已经排序,时间复杂度是 O(N+M)
如果两个关系需要排序,时间复杂度是对两个关系排序的成本:O(N*Log(N) + M*Log(M))
对于计算机极客,我给出下面这个可能的算法来处理多重匹配(注:对于这个算法我不保证100%正确):
mergeJoin(relation a, relation b) relation output integer a_key:=0; integer b_key:=0; while (a[a_key]!=null and b[b_key]!=null) if (a[a_key] < b[b_key]) a_key++; else if (a[a_key] > b[b_key]) b_key++; else //Join predicate satisfied write_result_in_output(a[a_key],b[b_key]) //We need to be careful when we increase the pointers if (a[a_key+1] != b[b_key]) b_key++; end if if (b[b_key+1] != a[a_key]) a_key++; end if if (b[b_key+1] == a[a_key] && b[b_key] == a[a_key+1]) b_key++; a_key++; end if end if end while
如果有最好的,就没必要弄那么多种类型了。这个问题很难,因为很多因素都要考虑,比如:
1 空闲内存:没有足够的内存的话就跟强大的哈希联接拜拜吧(至少是完全内存中哈希联接)。
2 两个数据集的大小。比如,如果一个大表联接一个很小的表,那么嵌套循环联接就比哈希联接快,因为后者有创建哈希的高昂成本;如果两个表都非常大,那么嵌套循环联接CPU成本就很高昂。
3 是否有索引:有两个 B+树索引的话,聪明的选择似乎是合并联接。
4 结果是否需要排序:即使你用到的是未排序的数据集,你也可能想用成本较高的合并联接(带排序的),因为最终得到排序的结果后,你可以把它和另一个合并联接串起来(或者也许因为查询用 ORDER BY/GROUP BY/DISTINCT 等操作符隐式或显式地要求一个排序结果)。
5 关系是否已经排序:这时候合并联接是最好的候选项。
6 联接的类型:是等值联接(比如 tableA.col1 = tableB.col2 )? 还是内联接?外联接?笛卡尔乘积?或者自联接?有些联接在特定环境下是无法工作的。
7 数据的分布:如果联接条件的数据是倾斜的(比如根据姓氏来联接人,但是很多人同姓),用哈希联接将是个灾难,原因是哈希函数将产生分布极不均匀的哈希桶。
8 如果你希望联接操作使用多线程或多进程。
想要更详细的信息,可以阅读相关数据库的文档。
我们已经研究了 3 种类型的联接操作。
现在,比如说我们要联接 5 个表,来获得一个人的全部信息。一个人可以有:
多个手机号(MOBILES)
多个邮箱(MAILS)
多个地址(ADRESSES)
多个银行账号(BANK_ACCOUNTS)
换句话说,我们需要用下面的查询快速得到答案:
MySQL SELECT * from PERSON, MOBILES, MAILS,ADRESSES, BANK_ACCOUNTS WHERE PERSON.PERSON_ID = MOBILES.PERSON_ID AND PERSON.PERSON_ID = MAILS.PERSON_ID AND PERSON.PERSON_ID = ADRESSES.PERSON_ID AND PERSON.PERSON_ID = BANK_ACCOUNTS.PERSON_ID
作为一个查询优化器,我必须找到处理数据最好的方法。但有 2 个问题:
每个联接使用那种类型?
我有 3 种可选(哈希、合并、嵌套),同时可能用到 0, 1 或 2 个索引(不必说还有多种类型的索引)。
按什么顺序执行联接?
比如,下图显示了针对 4 个表仅仅 3 次联接,可能采用的执行计划:
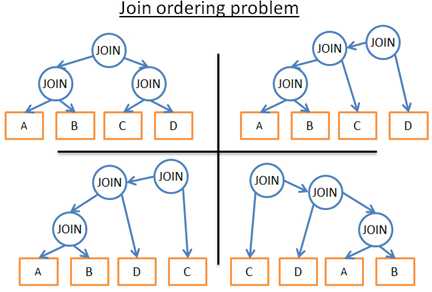
那么下面就是我可能采取的方法:
1) 采取粗暴的方式
用数据库统计,计算每种可能的执行计划的成本,保留最佳方案。但是,会有很多可能性。对于一个给定顺序的联接操作,每个联接有三种可能性:哈希、合并、嵌套,那么总共就有 3^4 种可能性。确定联接的顺序是个二叉树的排列问题,会有(2*4)!/(4+1)! 种可能的顺序。对本例这个相当简化了的问题,我最后会得到
3^4*(2*4)!/(4+1)! 种可能。
抛开专业术语,那相当于 27,216 种可能性。如果给合并联接加上使用 0,1 或 2 个 B+树索引,可能性就变成了 210,000种。我是不是告诉过你这个查询其实非常简单吗?
2) 我大叫一声辞了这份工作
很有诱惑力,但是这样一来,你不会的到查询结果,而我需要钱来付账单。
3) 我只尝试几种执行计划,挑一个成本最低的。
由于不是超人,我不能算出所有计划的成本。相反,我可以武断地从全部可能的计划中选择一个子集,计算它们的成本,把最佳的计划给你。
4) 我用聪明的规则来降低可能性的数量
有两种规则:
我可以用『逻辑』规则,它能去除无用的可能性,但是无法过滤大量的可能性。比如:
『嵌套联接的内关系必须是最小的数据集』。
我接受现实,不去找最佳方案,用更激进的规则来大大降低可能性的数量。比如:『如果一个关系很小,使用嵌套循环联接,绝不使用合并或哈希联接。』
在这个简单的例子中,我最后得到很多可能性。但现实世界的查询还会有其他关系运算符,像 OUTER JOIN, CROSS JOIN, GROUP BY, ORDER BY, PROJECTION, UNION, INTERSECT, DISTINCT … 这意味着更多的可能性。
那么,数据库是如何处理的呢?
动态规划,贪婪算法和启发式算法
关系型数据库会尝试我刚刚提到的多种方法,优化器真正的工作是在有限时间里找到一个好的解决方案。
多数时候,优化器找到的不是最佳的方案,而是一个『不错』的
对于小规模的查询,采取粗暴的方式是有可能的。但是为了让中等规模的查询也能采取粗暴的方式,我们有办法避免不必要的计算,这就是动态编程。
这几个字背后的理念是,很多执行计划是非常相似的。看看下图这几种计划:
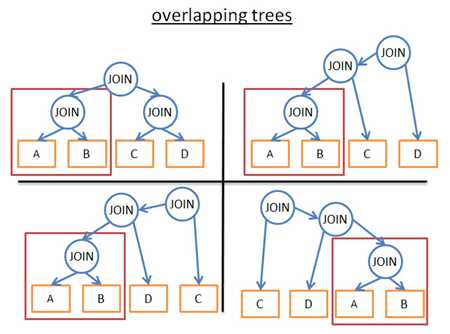
它们都有相同的子树(A JOIN B),所以,不必在每个计划中计算这个子树的成本,计算一次,保存结果,当再遇到这个子树时重用。用更正规的说法,我们面对的是个重叠问题。为了避免对部分结果的重复计算,我们使用记忆法。
应用这一技术,我们不再有 (2*N)!/(N+1)! 的复杂度,而是“只有” 3^N。在之前 4 个JOIN 的例子里,这意味着将 336 次排序降为 81 次。如果是大一些的查询,比如 8 个 JOIN (其实也不是很大啦),就是将 57,657,600 次降为 6551 次。【译者注:这一小段漏掉了,感谢nsos指出来。另外感谢 Clark Li 指出Dynamic Programing 应该翻译为动态规划。 】
对于计算机极客,下面是我在先前给你的教程里找到的一个算法。我不提供解释,所以仅在你已经了解动态规划或者精通算法的情况下阅读(我提醒过你哦):
procedure findbestplan(S) if (bestplan[S].cost infinite) return bestplan[S] // else bestplan[S] has not been computed earlier, compute it now if (S contains only 1 relation) set bestplan[S].plan and bestplan[S].cost based on the best way of accessing S /* Using selections on S and indices on S */ else for each non-empty subset S1 of S such that S1 != S P1= findbestplan(S1) P2= findbestplan(S - S1) A = best algorithm for joining results of P1 and P2 cost = P1.cost + P2.cost + cost of A if cost < bestplan[S].cost bestplan[S].cost = cost bestplan[S].plan = 『execute P1.plan; execute P2.plan; join results of P1 and P2 using A』 return bestplan[S]
针对大规模查询,你也可以用动态规划方法,但是要附加额外的规则(或者称为启发式算法)来减少可能性。
如果我们仅分析一个特定类型的计划(例如左深树 left-deep tree,参考),我们得到 n*2^n 而不是 3^n。
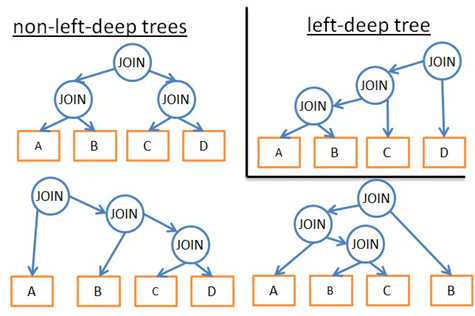
如果我们加上逻辑规则来避免一些模式的计划(像『如果一个表有针对指定谓词的索引,就不要对表尝试合并联接,要对索引』),就会在不给最佳方案造成过多伤害的前提下,减少可能性的数量。
如果我们在流程里增加规则(像『联接运算先于其他所有的关系运算』),也能减少大量的可能性。
……
但是,优化器面对一个非常大的查询,或者为了尽快找到答案(然而查询速度就快不起来了),会应用另一种算法,叫贪婪算法。
原理是按照一个规则(或启发)以渐进的方式制定查询计划。在这个规则下,贪婪算法逐步寻找最佳算法,先处理一条JOIN,接着每一步按照同样规则加一条新的JOIN。
我们来看个简单的例子。比如一个针对5张表(A,B,C,D,E)4次JOIN 的查询,为了简化我们把嵌套JOIN作为可能的联接方式,按照『使用最低成本的联接』规则。
直接从 5 个表里选一个开始(比如 A)
计算每一个与 A 的联接(A 作为内关系或外关系)
发现 “A JOIN B” 成本最低
计算每一个与 “A JOIN B” 的结果联接的成本(“A JOIN B” 作为内关系或外关系)
发现 “(A JOIN B) JOIN C” 成本最低
计算每一个与 “(A JOIN B) JOIN C” 的结果联接的成本 ……
最后确定执行计划 “( ( (A JOIN B) JOIN C) JOIN D ) JOIN E )”
因为我们是武断地从表 A 开始,我们可以把同样的算法用在 B,然后 C,然后 D, 然后 E。最后保留成本最低的执行计划。
顺便说一句,这个算法有个名字,叫『最近邻居算法』。
抛开细节不谈,只需一个良好的模型和一个 N*log(N) 复杂度的排序,问题就轻松解决了。这个算法的复杂度是 O(N*log(N)) ,对比一下完全动态规划的 O(3^N)。如果你有个20个联接的大型查询,这意味着 26 vs 3,486,784,401 ,天壤之别!
这个算法的问题是,我们做的假设是:找到 2 个表的最佳联接方法,保留这个联接结果,再联接下一个表,就能得到最低的成本。但是:
即使在 A, B, C 之间,A JOIN B 可得最低成本
(A JOIN C) JOIN B 也许比 (A JOIN B) JOIN C 更好。
为了改善这一状况,你可以多次使用基于不同规则的贪婪算法,并保留最佳的执行计划。
[ 如果你已经受够了算法话题,就直接跳到下一部分。这部分对文章余下的内容不重要。]【译者注:我也很想把这段跳过去 -_-f 】
很多计算机科学研究者热衷于寻找最佳的执行计划,他们经常为特定问题或模式探寻更好的解决方案,比如:
如果查询是星型联接(一种多联接查询),某些数据库使用一种特定的算法。
如果查询是并行的,某些数据库使用一种特定的算法。 ……
其他算法也在研究之中,就是为了替换在大型查询中的动态规划算法。贪婪算法属于一个叫做启发式算法的大家族,它根据一条规则(或启发),保存上一步找到的方法,『附加』到当前步骤来进一步搜寻解决方法。有些算法根据特定规则,一步步的应用规则但不总是保留上一步找到的最佳方法。它们统称启发式算法。
比如,基因算法就是一种:
一个方法代表一种可能的完整查询计划
每一步保留了 P 个方法(即计划),而不是一个。
0) P 个计划随机创建
1) 成本最低的计划才会保留
2) 这些最佳计划混合在一起产生 P 个新的计划
3) 一些新的计划被随机改写
4) 1,2,3步重复 T 次
5) 然后在最后一次循环,从 P 个计划里得到最佳计划。
循环次数越多,计划就越好。
这是魔术?不,这是自然法则:适者生存!
PostgreSQL实现了基因算法,但我并没有发现它是不是默认使用这种算法的。
数据库中还使用了其它启发式算法,像『模拟退火算法(Simulated Annealing)』、『交互式改良算法(Iterative Improvement)』、『双阶段优化算法(Two-Phase Optimization)』…..不过,我不知道这些算法当前是否在企业级数据库应用了,还是仅仅用在研究型数据库。
如果想进一步了解,这篇研究文章介绍两个更多可能的算法《数据库查询优化中联接排序问题的算法综述》,你可以去阅读一下。
[ 这段不重要,可以跳过 ]
然而,所有上述罗里罗嗦的都非常理论化,我是个开发者而不是研究者,我喜欢具体的例子。
我们来看看SQLite 优化器是怎么工作的。这是个轻量化数据库,它使用一种简单优化器,基于带有附加规则的贪婪算法,来限制可能性的数量。
SQLite 在有 CROSS JOIN 操作符时从不给表重新排序
使用嵌套联接
外联接始终按顺序评估
……
3.8.0之前的版本使用『最近邻居』贪婪算法来搜寻最佳查询计划
等等……我们见过这个算法!真是巧哈!
从3.8.0版本(发布于2015年)开始,SQLite使用『N最近邻居』贪婪算法来搜寻最佳查询计划
我们再看看另一个优化器是怎么工作的。IBM DB2 跟所有企业级数据库都类似,我讨论它是因为在切换到大数据之前,它是我最后真正使用的数据库。
看过官方文档后,我们了解到 DB2 优化器可以让你使用 7 种级别的优化:
对联接使用贪婪算法
0 – 最小优化,使用索引扫描和嵌套循环联接,避免一些查询重写
1 – 低级优化
2 – 完全优化
对联接使用动态规划算法
3 – 中等优化和粗略的近似法
5 – 完全优化,使用带有启发式的所有技术
7 – 完全优化,类似级别5,但不用启发式
9 – 最大优化,完全不顾开销,考虑所有可能的联接顺序,包括笛卡尔乘积
可以看到DB2 使用贪婪算法和动态规划算法。当然,他们不会把自己的启发算法分享出来的,因为查询优化器是数据库的看家本领。
DB2 的默认级别是 5,优化器使用下列特性: 【译者注:以下出现的一些概念我没有做考证,因为[ 这段不重要,可以跳过 ]】
使用所有可用的统计,包括线段树(frequent-value)和分位数统计(quantile statistics)。
使用所有查询重写规则(含物化查询表路由,materialized query table routing),除了在极少情况下适用的计算密集型规则。
使用动态规划模拟联接
有限使用组合内关系(composite inner relation)
对于涉及查找表的星型模式,有限使用笛卡尔乘积
考虑宽泛的访问方式,含列表预取(list prefetch,注:我们将讨论什么是列表预取),index ANDing(注:一种对索引的特殊操作),和物化查询表路由。
默认的,DB2 对联接排列使用受启发式限制的动态规划算法。
其它情况 (GROUP BY, DISTINCT…) 由简单规则处理。
由于创建查询计划是耗时的,大多数据库把计划保存在查询计划缓存,来避免重复计算。这个话题比较大,因为数据库需要知道什么时候更新过时的计划。办法是设置一个上限,如果一个表的统计变化超过了上限,关于该表的查询计划就从缓存中清除。
在这个阶段,我们有了一个优化的执行计划,再编译为可执行代码。然后,如果有足够资源(内存,CPU),查询执行器就会执行它。计划中的操作符 (JOIN, SORT BY …) 可以顺序或并行执行,这取决于执行器。为了获得和写入数据,查询执行器与数据管理器交互,本文下一部分来讨论数据管理器。
标签:job 中间 文档 from else 优化器 排列 ntile 新版
原文地址:https://www.cnblogs.com/qixinbo/p/9385368.html