用最通俗的语言让你学会网络流

标签：for   algo   进制   水平   接下来   关注   space   表示   小流量   

我们想象一下自来水厂到你家的水管网是一个复杂的有向图，每一节水管都有一个最大承载流量。自来水厂不放水，你家就断水了。但是就算自来水厂拼命的往管网里面注水，你家收到的水流量也是上限（毕竟每根水管承载量有限）。你想知道你能够拿到多少水，这就是一种网络流问题。

在网上找了很久资料，虽然讲解网络流的资料很多但是浅显易懂的很少（可能是我太蒻了吧），写这篇文章只希望点进来的人都能学会网络流（都能点赞）

我尽量用通俗易懂的语言讲解，同时结合图示理解。

我将讲解以下网络流算法：

1. 最大流

2. 最小费用最大流

先从最基础的最大流开始：

何为最大流问题？

简单来说就是水流从一个源点s通过很多路径，经过很多点，到达汇点t，问你最多能有多少水能够到达t点。

结合图示理解：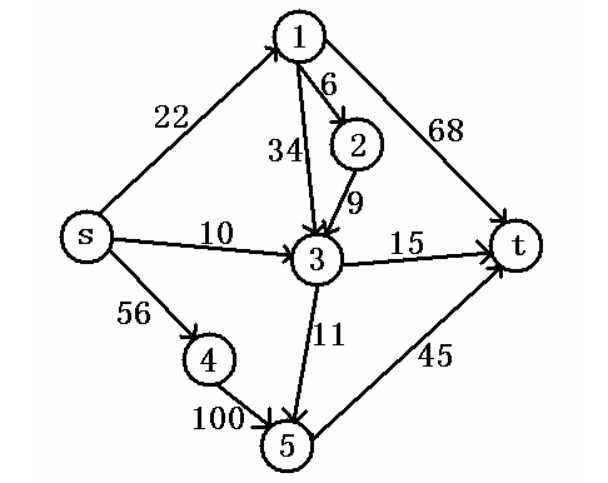

从s到t经过若干个点，若干条边，每一条边的水流都不能超过边权值（可以小于等于但不能大于），所以该图的最大流就是10+22+45=77。

如果你还是不能理解，我们就换一种说法，假设s城有inf个人想去t城，但是从s到t要经过一些城市才能到达，（以上图为例）其中s到3城的火车票还剩10张，3到t的火车票还剩15张，其他路以此类推，问最终最多能有多少人能到达t城？（假设这个地区只有火车，没有汽车飞机，步行和骑自行车会累死就不考虑了，再假设所有人都买得起火车票。）

那怎么么解决这个问题呢？

对于这个问题，刚看到时，你有什么想法？

或许你会有一个这样的思路：从s开始找所有能到达t的路径，然后找每条路径上权值最小的边（或者说能承受水流最小的管子），再进行其它操作，就能找到这张图的最大流。

然后我们有

EK（Edmond—Karp）算法。

其实还有其它算法，但由于过于复杂（作者太懒不想画图），（以作者的语文水平）很难讲的通俗易懂，就不献丑了。

这里我就不介绍那么多公式定理之类的了（为了通俗易懂，并且不把你绕晕），为方便讲解，引入一个概念：

增广路：

增广路是指从s到t的一条路，流过这条路，使得当前的流（可以到达t的人）可以增加。

那么求最大流问题可以转换为不断求解增广路的问题，并且，显然当图中不存在增广路时就达到了最大流。

具体怎么操作呢？

其实很简单，直接从s到t广搜即可，从s开始不断向外广搜，通过权值大于0的边（因为后面会减边权值，所以可能存在边权为0的边），直到找到t为止，然后找到该路径上边权最小的边，记为mi，然后最大流加mi，然后把该路径上的每一条边的边权减去mi，直到找不到一条增广路（从s到t的一条路径）为止。（为什么要用mi呢？你要争取在这条路上多走更多人，但又不能让人停在某个城市）

具体操作：

找增广路：

bool bfs(){
    queue<int>q;
    memset(inque,0,sizeof(inque));
    memset(pre,-1,sizeof(pre));
    inque[s]=1;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=node[i].next){
            int d=node[i].v;
            if(!inque[d]&&node[i].val){//node[i].val==0则已经该路径满了
            inque[d]=1;
            pre[d].v=u;
            pre[d].edge=i;
            if(d==t)return 1;
            q.push(d);
            }
        }
    }
    return 0;
}//是否有增广路 

那个pre数组是由来记录路径的，它长这样：

struct Pre{
    int v;//该点的前一个点（从起点过来） 
    int edge;//与该点相连的边（靠近起点的） 
}pre[101010];

然后直接累加最大流（注意加的时候要把改边边权减去相应的流量，防止一直重复加同一段流）

那代码是长这样的吗?

int EK(){
    int ans=0;
    while(bfs()){
        int mi=inf;
        for(int i=t;i!=s;i=pre[i].v){
        mi=min(mi,node[pre[i].edge].val);
        }
        for(int i=t;i!=s;i=pre[i].v){
        node[pre[i].edge].val-=mi;
        }
        ans+=mi;
    }
    return ans;
}

当然不是，万一第一次流错了使得这样的流法无法得到最大流怎么办？ 还是以刚才那张图为例，为了防止你再翻上去，我直接再放一次：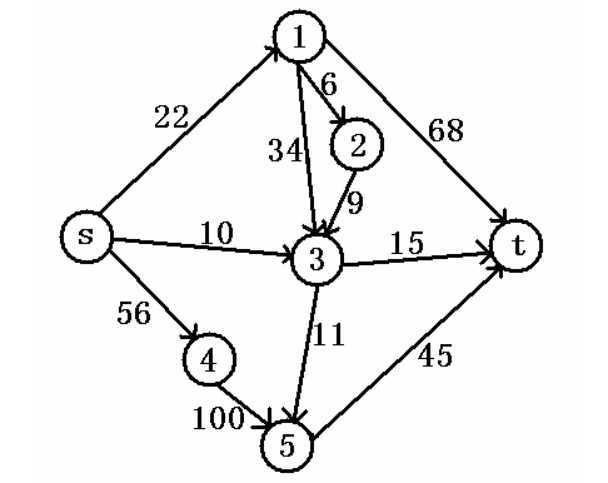

如果你第一次的增广路是：s->3->5->t流量显然是10，第二次的增广路是s->4->5->t流量显然是35（因为5->t的流量有10点被3号点来的人占领了)。

而这种方案显然不如：s->4->5->t流量为45，s->3->t流量为10。

那程序怎么知道哪种方案最优？

它当然不知道，我们要把所有情况都找一遍，难道要回溯？

当然不，这里使用一种高级技巧，加反向边。什么意思？

以下图为例：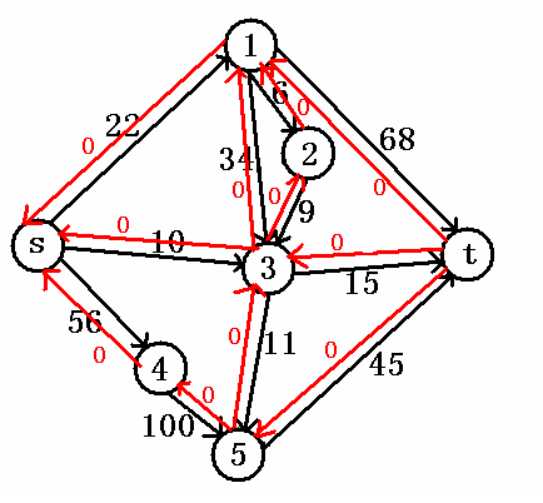

这是刚才那张图，我们在每条边都加了一条反向的，权值为0的边（红色的边）。

有什么用呢？

占空间？拖时间？显然不是。

先不管有什么用，加了反向边，我们再跑一次EK，这次，除了要给增广路上的边都减去该路上的最小流量以外，还要给反向边加上最小流量。为什么？先别管。

先找增广路，比如说我们走了s->3->5->t，那么图会变成：

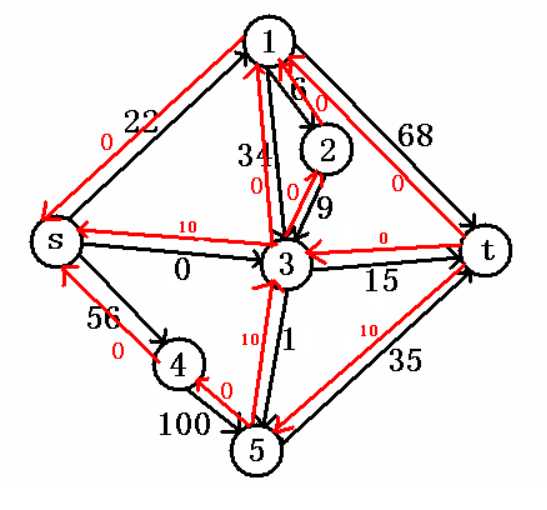
再找一次增广路，这次比如说我们走s->4->5->t。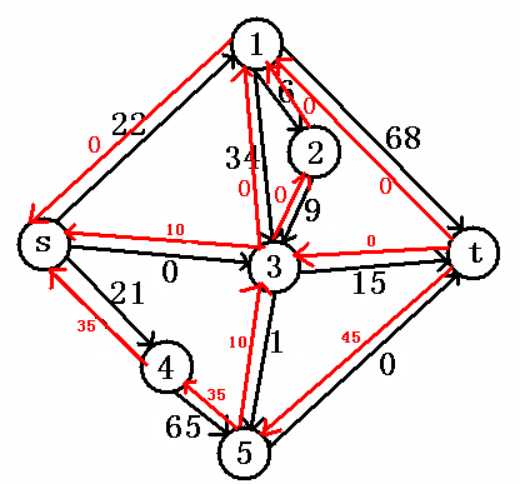

再找一次增广路，这次我们找s->4->5->3->t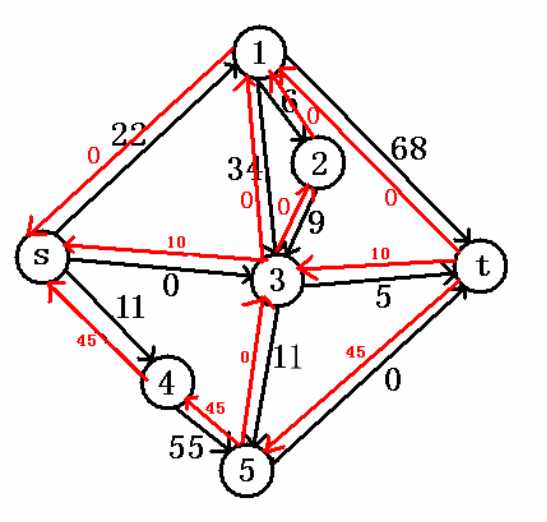

好像有点奇怪。你可能会想：为什么这次搜索的时候走了反向边（红色）的边，为什么走了反向边（红色）的边会加正向边（黑色）的边？

这就好像是45个人沿着s->4->5->t的路线想去t城，到了5城却发现有10个来自3城的人先定了5->t的票！他们十分焦急，总不能让他们在5城等吧。

怎么办呢？他们通过反向边上的标记发现了那10个人是来自3城的，利用标记，他们发现那10个人可以直接从3城到t城，于是他们（利用了哆啦A梦的时光机）告诉还在3城时的那10个人可以直接走3->t这条路，然后他们就可以买到空出来的5->t的10张票了。

现在你知道反向边的作用了吧：留下一个标记，让后面的人有机会让前面的人走另一条路。

理解了反向边的作用，恭喜你已经理解了EK求解最大流算法的原理了。

下面讲解关于反向边在代码中的实现：

关于反向边在加正向边时要一起加上，边权为0，然后在寻找增广路时就没必要关注一条边是正向边还是反向边了，在统计最大流时，要把每一条经过的边的边权减去这条增广路的流（最小流量），每条经过的边的反向边（反向边的反向边是正向边，负负得正）加上这条增广路的流。

现在还有一个小问题，怎么通过一条边的编号求它的反向边的编号。

由于正向边和反向边是一起加的，所以反向边的编号与正向边的编号只相差1。

那就好办了。

如果第一条边的编号是偶数，就有

正向边的编号^1==反向边的编号；反向边的编号^1==正向边的编号。（？为什么？）

那么接下来就来证明：当正向边的编号为2n时反向边的编号为2n+1。设n的二进制表示为XXXXX，则2n==n<<1 因此2n的二进制表示:XXXXX0,而2*n+1的二进制表示：XXXXX1。 那肯定（2n）^1==2n+1;(2n+1）^1==2n。

都讲完了，那就附上完整代码：

//EK算法求解最大流 
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int inf=1<<30;
int n,m,s,t;
struct Node{
    int v;
    int val;
    int next;
}node[201010];
int top=1,head[101010];//top必须从一个奇数开始，一般用-1但我不习惯，解释见下方 
inline void addedge(int u,int v,int val){
    node[++top].v=v;
    node[top].val=val;
    node[top].next=head[u];
    head[u]=top;
}
inline int Read(){
    int x=0;
    char c=getchar();
    while(c>‘9‘||c<‘0‘)c=getchar();
    while(c>=‘0‘&&c<=‘9‘)x=x*10+c-‘0‘,c=getchar();
    return x;
}
int inque[101010];//点是访问过里 
struct Pre{
    int v;//该点的前一个点（从起点过来） 
    int edge;//与该点相连的边（靠近起点的） 
}pre[101010];
inline bool bfs(){
    queue<int>q;
    memset(inque,0,sizeof(inque));
    memset(pre,-1,sizeof(pre));
    inque[s]=1;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=node[i].next){
            int d=node[i].v;
            if(!inque[d]&&node[i].val){//node[i].val==0则已经该路径满了 
            pre[d].v=u;
            pre[d].edge=i;
            if(d==t)return 1;
            inque[d]=1;
            q.push(d);
            }
        }
    }
    return 0;
}//是否有增广路 
int EK(){
    int ans=0;
    while(bfs()){
        int mi=inf;
        for(int i=t;i!=s;i=pre[i].v){
            mi=min(mi,node[pre[i].edge].val);//每次只能增加增广路上最小的边的权值 
        }
        for(int i=t;i!=s;i=pre[i].v){
            node[pre[i].edge].val-=mi;
            node[pre[i].edge^1].val+=mi;
            //反向的边的编号是正向边的编号^1
            //这就是为什么top开始时必须是奇数 
        }
        ans+=mi;
    }
    return ans;
}
int main(){
    register int i;
    n=Read(),m=Read(),s=Read(),t=Read();
    int u,v,w;
    for(i=1;i<=m;i++)
    u=Read(),v=Read(),w=Read(),addedge(u,v,w),addedge(v,u,0);
    printf("%d",EK());
    return 0;
}

题目是：【模板】网络最大流

那么这个（乱七八糟的）算法有什么用呢？

经典应用：二分图匹配。

什么意思？

给两个集合：A，B，其中A有一些元素a1,a2,a3……，B有一些元素b1,b2,b3……

其中a1想和b1，b4，……中的一个配对，a2想和b1，b250，b2500……（这些数字没什么特别含义）配对，为最优情况下能有多少组配对成功。

二分匹配模板题： 飞行员配对方案问题

怎么做呢？

其实二分匹配问题可以转换为网络流问题。

把集合A当成起点，集合B当成终点，若集合一中元素a可以对应集合二中元素b，则加一条a指向b流量为一的边

新增加两个点，s和t，s有指向所有起点的边，所有终点有指向t的边，只需计算s到t的最大流，用EK算法即可。

本题要求记录配对方案，只需在找增广路时加个标记即可。

附上代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
int n,m;
const int mx=1<<30;
struct Node{
    int v;
    int val;
    int nxt;
}node[5010];
int top=1;
int s=1008,t=1009;
int ansk[1050];//标号为i的外籍飞行员和标号为ansk[i]-n的英国飞行员对应 
struct P{
    int fa;
    int edge;
}pre[1010];//在一条增广路中，节点的前一个节点和与之相连的边 
int head[1010];
int inque[1010];
inline int Read(){
    int x=0,f=1;
    char c=getchar();
    while(c>‘9‘||c<‘0‘){
        if(c==‘-‘)f=-1;
        c=getchar();
    }
    while(c>=‘0‘&&c<=‘9‘)x=x*10+c-‘0‘,c=getchar();
    return x*f;
}
inline void addedge(int u,int v,int val){
    node[++top].v=v;
    node[top].val=val;
    node[top].nxt=head[u];
    head[u]=top;
}
bool addroad(){
    memset(pre,-1,sizeof(pre));
    memset(inque,0,sizeof(inque));
    queue<int>q;
    q.push(s);
    inque[s]=1;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=node[i].nxt){
            int d=node[i].v;
            int val=node[i].val;
            if(val!=0&&inque[d]==0){
                pre[d].fa=u;
                pre[d].edge=i;
                if(d==t)return 1;
                q.push(d);
                inque[d]=1;
            }
        }
    }
    return 0;
}//寻找增广路 
int EK(){
    int ans=0;
    while(addroad()){
        int mi=mx;
        for(int i=t;i!=s;i=pre[i].fa)mi=min(mi,node[pre[i].edge].val);
        for(int i=t;i!=s;i=pre[i].fa)ansk[pre[i].fa]=i,node[pre[i].edge].val-=mi,node[pre[i].edge^1].val+=mi;
        ans+=mi;
    }
    return ans;
}//EK求最大流
int main(){
    m=Read(),n=Read();
    register int i;
    //英国飞行员用n+i号点表示，外籍飞行员用i号点表示 
    for(i=1;i<=n;i++)addedge(i+n,t,1),addedge(t,i+n,0);//使所有英国空军和汇点相连 
    for(i=1;i<=m;i++)addedge(s,i,1),addedge(i,s,0);//使所有外籍空军和源点相连
    int u,v;
    while(1){
    u=Read(),v=Read();
    if(u==-1&&v==-1)break;
    addedge(u,v+n,1);
    addedge(v+n,u,0);
    } 
    printf("%d\n",EK());
    for(i=1;i<=n;i++)if(ansk[i]!=0)printf("%d %d\n",i,ansk[i]-n);
    return 0;
}

其实相比于网络流，二分匹配还有更快的方法，匈牙利算法，这里就不详细讲解了，今天的重点是网络流。

对于这道题，网络流会超时，匈牙利算法不会超时： 【模板】二分图匹配

感兴趣的可以自行研究，还是给出代码吧：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
int n,m,e;
int to[1010][1010];
int used[1010],y[1010];//m集合中的点是否使用过，若使用过，与它匹配的是谁 
inline int Read(){
    int x=0;
    char c=getchar();
    while(c>‘9‘||c<‘0‘)c=getchar();
    while(c>=‘0‘&&c<=‘9‘)x=x*10+c-‘0‘,c=getchar();
    return x;
}
int find(int x){
    for(register int i=1;i<=m;i++){
        if(to[x][i]==1&&used[i]==0){
            used[i]=1;
            if(y[i]==0||find(y[i])==1){
                y[i]=x;
            return 1;
            }
     }
    }
    return 0;
}
int findans(){
    int ans=0;
    for(register int i=1;i<=n;i++){
        memset(used,0,sizeof(used));
        ans+=find(i);
    }
    return ans;
}
int main(){
    n=Read(),m=Read(),e=Read();
    register int i;
    int u,v;
    for(i=1;i<=e;i++){
        u=Read(),v=Read();
        if(u>n)continue;
        if(v>m)continue;
        to[u][v]=1;
    }
    printf("%d",findans());
    return 0;
}

然后就是最小费用最大流了

听名字就和上面讲的差不多。

什么是最小费用最大流呢？

以下图为例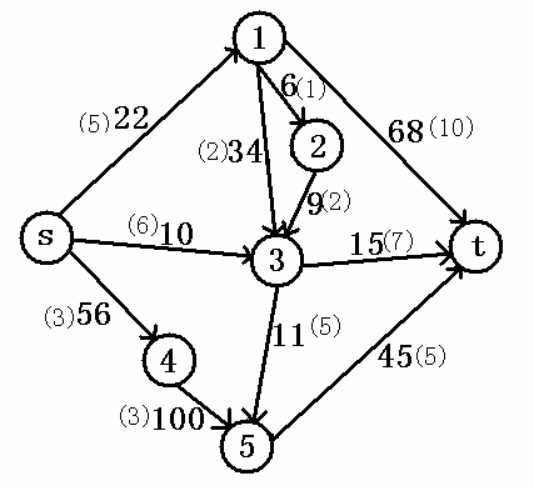

上图中没打（）的为边权（最大流量），打（）的为单位流量的价格

还是用刚才那种通俗易懂的解释方法

假设s城有inf个（穷）人想去t城，但是从s到t要经过一些城市才能到达，其中s到3城的火车票还剩10张票价为6元/人，3到t的火车票还剩15张票价为7元/人，其他路以此类推，问最终最多能有多少人能到达t城？

（由于是穷人）他们希望能在最多人到达t城的同时花最少的钱，问最少的钱是多少？

有了刚才学习最大流的基础，相信接下来的讲解应该很容易看懂。

还是找增广路的思想，但是这次我们找花费最小（即s到t费用最小）的增广路。

怎么实现呢？

看到那个（即s到t费用最小）了吗？

想到了什么？

最短路算法！

也就是说我们在找增广路时，把bfs换成spfa就可以了！

附上代码（相信看到这里，不用看我打的代码你都能自己打出来了）：

bool spfa(){
    memset(pre,0,sizeof(pre));
    memset(dist,0x3f,sizeof(dist));
    memset(inque,0,sizeof(inque));
    queue<int>q;
    q.push(s);
    inque[s]=1;
    dist[s]=0;
    while(!q.empty()){
        int u=q.front();
        inque[u]=0;
        q.pop();
        register int i,d,w;
        for(i=head[u];i;i=node[i].next){
            d=node[i].v;
            w=node[i].w;
            if(node[i].val&&dist[d]>dist[u]+w){
            //这里dist表示从s到某个点d的单位最小费用
                dist[d]=dist[u]+w;
                pre[d].fa=u;
                pre[d].adge=i;
                if(inque[d]==0){
                    q.push(d);
                    inque[d]=1;
                }
            }
        }
    }
    return dist[t]!=0x3f3f3f3f;
}//寻找费用最小的增广路

还有一点要注意：反向边的花费为正向边的相反数。

？

其实很好理解，如果那几个人不走这条路，那么这条路的钱就不用花了，但是因为刚才（前面走过的增广路）走过时花了钱，这次走反向边要退钱。

然后就是计算最大流和对应的最小费用了

int EK(){//最小费用最大流的EK算法
    maxflow=0;
    cost=0;
    int mi;
    register int i;
    while(spfa()){
        mi=inf;
        for(i=t;i!=s;i=pre[i].fa)mi=min(mi,node[pre[i].adge].val);
        for(i=t;i!=s;i=pre[i].fa){
            node[pre[i].adge].val-=mi;
            node[pre[i].adge^1].val+=mi;
        }
        maxflow+=mi;
        cost+=mi*dist[t];
        //本增广路最多能流的流量*从s到t的单位费用
    }
    return maxflow;
}

这道题是 【模板】最小费用最大流

附上完整代码：

//EK算法求解最小费用最大流
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<queue>
using namespace std;
int maxflow;//最大流
int cost;//最小费用 
int top=1,head[5010];
const int inf=1<<30;
int dist[5010];
int inque[5010];
int n,m,s,t;
struct Node{
    int v;
    int w;//该边单位流量的费用
    int next;
    int val;//该边最大流量 
}node[101100];
struct P{
    int fa;//增广路上该点的父亲 
    int adge;//该点与父亲相连的边的编号 
}pre[5010];
inline int Read(){
    int x=0;
    char c=getchar();
    while(c>‘9‘||c<‘0‘)c=getchar();
    while(c>=‘0‘&&c<=‘9‘)x=x*10+c-‘0‘,c=getchar();
    return x;
}
inline void addedge(int u,int v,int val,int w){
    node[++top].v=v;
    node[top].val=val;
    node[top].w=w;
    node[top].next=head[u];
    head[u]=top;
}
bool spfa(){
    memset(pre,0,sizeof(pre));
    memset(dist,0x3f,sizeof(dist));
    memset(inque,0,sizeof(inque));
    queue<int>q;
    q.push(s);
    inque[s]=1;
    dist[s]=0;
    while(!q.empty()){
        int u=q.front();
        inque[u]=0;
        q.pop();
        register int i,d,w;
        for(i=head[u];i;i=node[i].next){
            d=node[i].v;
            w=node[i].w;
            if(node[i].val>0&&dist[d]>dist[u]+w){
                dist[d]=dist[u]+w;
                pre[d].fa=u;
                pre[d].adge=i;
                if(inque[d]==0){
                    q.push(d);
                    inque[d]=1;
                }
            }
        }
    }
    return dist[t]!=0x3f3f3f3f;
}//寻找费用最小的增广路
int EK(){//最小费用最大流的EK算法
    maxflow=0;
    cost=0;
    int mi;
    register int i;
    while(spfa()){
        mi=inf;
        for(i=t;i!=s;i=pre[i].fa)mi=min(mi,node[pre[i].adge].val);
        for(i=t;i!=s;i=pre[i].fa){
            node[pre[i].adge].val-=mi;
            node[pre[i].adge^1].val+=mi;
        }
        maxflow+=mi;
        cost+=mi*dist[t];
    }
    return maxflow;
}
int main(){
    n=Read(),m=Read(),s=Read(),t=Read();
    register int i;
    int u,v,val,w;
    for(i=1;i<=m;i++){
        u=Read(),v=Read(),val=Read(),w=Read();
        addedge(u,v,val,w);
        addedge(v,u,0,-w);
    }
    printf("%d ",EK());
    printf("%d",cost);
    return 0;
}

另外，最小费用最大流还有更高效的zkw算法，由于有点复杂（作者太懒）就不讲解的，感兴趣的自行百度。

用最通俗的语言让你学会网络流

标签：for   algo   进制   水平   接下来   关注   space   表示   小流量   

原文地址：https://www.cnblogs.com/Star-Dragon/p/9386448.html