一堆乱七八糟绝不正经的排序算法

标签：names   std   nothing   作品   html   部落   length   最大   詹姆斯   

原文

索引

1. 猴子排序

2. 钻石排序（戴蒙德排序）

3. 恶魔排序

4. 珠排序

5. 地精排序（怂货排序）

6. 智能设计排序

1. 猴子排序

（提供者cy1306110516）

猴子排序的思想源自于著名的无限猴子定理。

既然猴子们能敲出《哈姆雷特》，区区排序又算什么呢？

思路：

1. 判断数组是否有序，如果无序，进入下一步。

2. 随机打乱数组，回到上一步。

适用人群：

欧皇

时间复杂度：

• 最坏情况O(∞)

• 最好情况O(n)

算法实现：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 int n,a[100005];
 4 inline void random_(){
 5     for (int i=1;i<=n;i++) swap(a[i],a[i+rand()%(n-i+1)]);
 6     //打乱，AC全靠RP
 7 }
 8 inline bool check(){
 9     for (int i=2;i<=n;i++) if (a[i]<a[i-1]) return false;
10     return true;
11     //判断是否有序
12 }
13 inline void bogo_sort(){
14     while (!check())
15     random_();
16     //核心代码
17 }
18 int main(){
19     scanf("%d",&n);
20     srand(time(NULL));
21     for (int i=1;i<=n;i++) scanf("%d",&a[i]);
22     bogo_sort();
23     for (int i=1;i<=n;i++) printf("%d ",a[i]);
24     return 0;
25 }//提供者cy1306110516

2. 钻石排序

（提供者DARTH_VADER）

钻石排序（又名戴蒙德排序）的思想源自于演化生物学家贾雷德·戴蒙德的作品《枪炮、病菌与钢铁》。

思路：

1. 对于数组中的每一项，创造一个等同人数的人类部落。

2. 让他们独立地发展。

3. 第一个发展出枪支的最大，以此类推。

适用人群：

极远未来的统治阶层

时间复杂度：

O(n)，常数为13000年。

代码实现：

暂无

3.恶魔排序

（提供者DARTH_VADER）

恶魔排序的思想源自于十九世纪英国物理学家詹姆斯·克拉克·麦克斯韦的麦克斯韦恶魔假说。

思路：

创造这样的一种气体：其每一个分子运动速度与数组中的每一个数成比例。

将这样的气体灌入一个密封的盒子，该盒子被一分为二，中间有一个小孔接通两侧。

小孔一次只能经过一个分子。

每一次迅速打开小孔，让特定分子经过。

那么长时间后，盒子将一侧热一侧冷。

对于每一侧，分治进行本算法。

适用人群：

麦克斯韦的恶魔

时间复杂的：

O(n!)

代码实现：

暂无

4. 珠排序

（提供者502_Bad_Gateaway）

珠排序的思想源自于中国历史悠久的算盘。（大雾）

思路：

1. 对于每一个数字，我们用一排珠子表示。

2. 将这些珠子叠在一起，使其自然下落。

3. 每一层的珠子数量即为该位置数值。

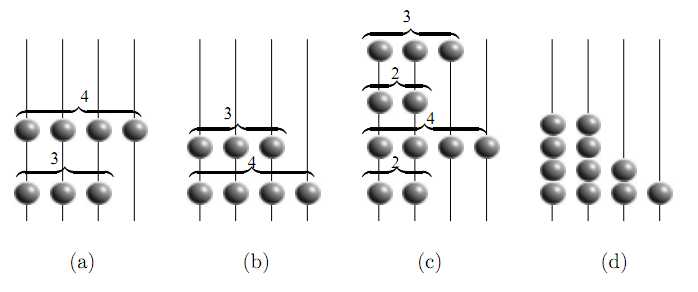
适用人群：

喜好珠算的OIer

时间复杂度：

这个。。。呃呃呃看你怎么说了

代码实现：

等一下哈，本人正在敲

5. 怂货地精排序

（提供者502_Bad_Gateaway）

怂货排序。。。很怂。

思路：

1. 当i=0或a[i]>a[i-1]时，i++。

2. 否则交换a[i]与a[i-1]，i--。

适用人群：

正常人类

时间复杂度：

O( n^2n2 )

代码实现：

 1 void gnome_sort(int unsorted[]){
 2     int i = 0;
 3     while (i < unsorted.Length){
 4         if (i == 0 || unsorted[i - 1] <= unsorted[i])i++;
 5         else{
 6             int tmp = unsorted[i];
 7             unsorted[i] = unsorted[i - 1];
 8             unsorted[i - 1] = tmp;
 9             i--;
10         }
11     }
12 }//提供者DARTH_VADER

6. 智能设计排序

（提供者DARTH_VADER）

智能设计排序的思想源自于智能设计论（智设论）。

思路：

假设我们有一些数字（它们组成了给出的数组），那么它们恰好排序成给出的数组的概率是 \frac{1}{n!}n!1?。

面对如此小的可能性，我们断言这样的数组是随机出现的，未免太过果断。

有理由相信，这样的一个数组是一个有自我意志的排序者给出的。

由于我们对排序的认知被局限在递增或递减，揣摩排序者用意的行为是不理智的。

因此大可放心：数组已被排序！

适用人群：

懒人

时间复杂度：

O(0)，当然算上输入就是O(n)

代码实现：

1 #define donothing return
2 void intelligentDesignSort(int list[]){
3     donothing;
4 }//提供者DARTH_VADER
5  

一堆乱七八糟绝不正经的排序算法

标签：names   std   nothing   作品   html   部落   length   最大   詹姆斯   

原文地址：https://www.cnblogs.com/bztMinamoto/p/9392571.html