c/c++ 用普利姆（prim）算法构造最小生成树

标签：连通   图片   经济   --   不能   prim   最小生成树   move   turn   

c/c++ 用普利姆（prim）算法构造最小生成树

最小生成树（Minimum Cost Spanning Tree）的概念：

? 假设要在n个城市之间建立公路，则连通n个城市只需要n-1条线路。这时，自然会考虑，如何在最节省经费的前提下建立这个公路网络。

? 每2个城市之间都可以设置一条公路，相应地都要付出一定的经济代价。n个城市之间，最多可以设置n(n-1)/2条线路，那么，如何在这些可能的线路中选择n-1条，以使总的耗费最少？

普利姆（prim）算法的大致思路：

? 大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

用图示和代码说明：

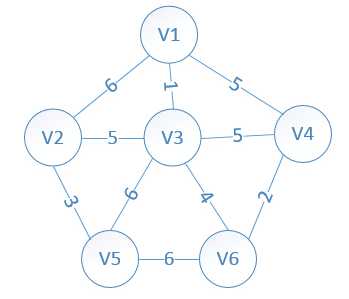
初始状态：

设置2个数据结构：

lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST

mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=0表示起点i加入MST

我们假设V1是起始点，进行初始化（*代表无限大，即无通路）：

lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=，lowcost[6]=

mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）

明显看出，以V3为终点的边的权值最小=1，所以边<mst[3],3>=1加入MST

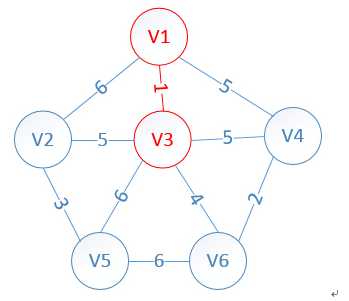
此时，因为点V3的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4

mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3

明显看出，以V6为终点的边的权值最小=4，所以边<mst[6],6>=4加入MST

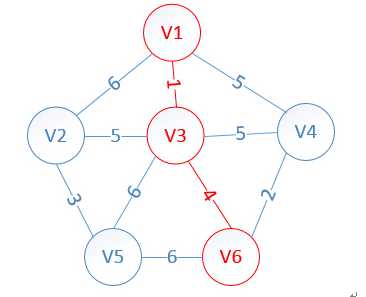
此时，因为点V6的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0

明显看出，以V4为终点的边的权值最小=2，所以边<mst[4],4>=4加入MST

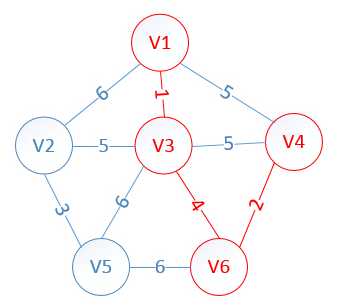
此时，因为点V4的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=0，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=0，mst[5]=3，mst[6]=0

明显看出，以V2为终点的边的权值最小=5，所以边<mst[2],2>=5加入MST

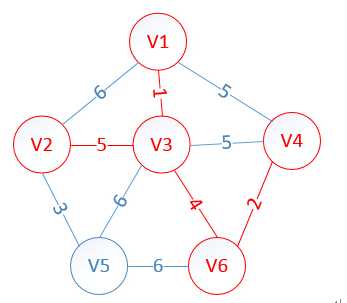
此时，因为点V2的加入，需要更新lowcost数组和mst数组：

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=3，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=2，mst[6]=0

很明显，以V5为终点的边的权值最小=3，所以边<mst[5],5>=3加入MST

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=0，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=0，mst[6]=0

至此，MST构建成功，如图所示：

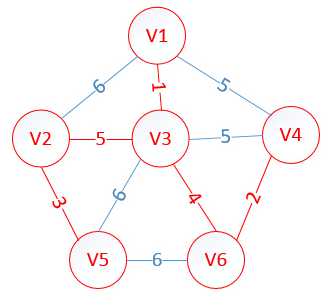
mixSpanTree.h

#ifndef __mixspantree__
#define __mixspantree__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>

#define Default_vertex_size 20

#define T char//dai biao ding dian de lei xing
#define E int
#define MAX_COST 0x7FFFFFFF


typedef struct GraphMtx{
  int MaxVertices;//zui da ding dian shu liang]
  int NumVertices;//shi ji ding dian shu liang
  int NumEdges;//bian de shu lian

  T* VerticesList;//ding dian list
  int** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1
}GraphMtx;

//chu shi hua tu
void init_graph(GraphMtx* gm);
//打印二维数组
void show_graph(GraphMtx* gm);
//插入顶点
void insert_vertex(GraphMtx* gm, T v);
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost);
//删除顶点
void remove_vertex(GraphMtx* gm, T v);
//删除顶点间的线
void remove_edge(GraphMtx* gm, T v1, T v2);
//摧毁图
void destroy_graph(GraphMtx* gm);
//取得与v顶点有连线的第一个顶点
int getNeighbor(GraphMtx* gm, T v);
//取得与v1顶点，v1顶点之后的v2顶点的之后的有连线的第一个顶点
int getNextNeighbor(GraphMtx* gm, T v1, T v2);

//用prim算法作成最小树
void minSpanTree_prim(GraphMtx* gm, T v);
//取得2个顶点间的权重
E getWeight(GraphMtx* g, int i1, int i2);

#endif

mixSpanTree.c

#include "mixSpanTree.h"

void init_graph(GraphMtx* gm){
  gm->MaxVertices = Default_vertex_size;
  gm->NumEdges = gm->NumVertices = 0;

  //kai pi ding dian de nei cun kong jian
  gm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));
  assert(NULL != gm->VerticesList);

  //创建二维数组
  //让一个int的二级指针，指向一个有8个int一级指针的数组
  //开辟一个能存放gm->MaxVertices个int一级指针的内存空间
  gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));
  assert(NULL != gm->Edge);
  //开辟gm->MaxVertices组，能存放gm->MaxVertices个int的内存空间
  for(int i = 0; i < gm->MaxVertices; ++i){
    gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);
  }
  //初始化二维数组
  //让每个顶点之间的边的关系都为不相连的
  for(int i = 0; i < gm->MaxVertices; ++i){
    for(int j = 0; j < gm->MaxVertices; ++j){
      if(i == j)
    gm->Edge[i][j] = 0;
      else
    gm->Edge[i][j] = MAX_COST;
    }
  }
}
//打印二维数组
void show_graph(GraphMtx* gm){
  printf("  ");
  for(int i = 0; i < gm->NumVertices; ++i){
    printf("%c  ", gm->VerticesList[i]);
  }
  printf("\n");
  for(int i = 0; i < gm->NumVertices; ++i){
    //在行首,打印出顶点的名字
    printf("%c:", gm->VerticesList[i]);
    for(int j = 0; j < gm->NumVertices; ++j){
      if(gm->Edge[i][j] == MAX_COST){
    printf("%c  ", ‘*‘);
      }
      else{
    printf("%d  ", gm->Edge[i][j]);
      }
    }
    printf("\n");
  }
  printf("\n");
}
//插入顶点
void insert_vertex(GraphMtx* gm, T v){
  //顶点空间已满，不能再插入顶点了
  if(gm->NumVertices >= gm->MaxVertices){
    return;
  }
  gm->VerticesList[gm->NumVertices++] = v;
}

int getVertexIndex(GraphMtx* gm, T v){
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->VerticesList[i] == v)return i;
  }
  return -1;
}
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost){
  if(v1 == v2)return;
  
  //查找2个顶点的下标
  int j = getVertexIndex(gm, v1);
  int k = getVertexIndex(gm, v2);
  //说明找到顶点了,并且点之间还没有线
  if(j != -1 && k != -1 ){
    //因为是无方向，所以更新2个值
    gm->Edge[j][k] = gm->Edge[k][j] = cost;
    //边数加一
    gm->NumEdges++;
  }
}
//删除顶点间的线
void remove_edge(GraphMtx* gm, T v1, T v2){
  if(v1 == v2)return;
  //查找2个顶点的下标
  int j = getVertexIndex(gm, v1);
  int k = getVertexIndex(gm, v2);
  //说明找到顶点了,并且点之间还有线
  if(j != -1 && k != -1 && gm->Edge[j][k] == 1){
    //因为是无方向，所以更新2个值
    gm->Edge[j][k] = gm->Edge[k][j] = 0;
    //边数减一
    gm->NumEdges--;
  }
}
//删除顶点
void remove_vertex(GraphMtx* gm, T v){
  int k = getVertexIndex(gm, v);
  if(-1 == k)return;
  
  //算出和要删除节点相关的边的数量，并减少。
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->Edge[k][i] == 1){
      gm->NumEdges--;
    }
  }

  //如果要删除的顶点不是最后一个顶点
  if(k != gm->NumVertices - 1){
    //把每一列向左移动一列
    for(int i = 0; i < gm->NumVertices; ++i){
      //把后面内存里的内容移动到前面，并把最后一个元素设置成0
      memmove(&(gm->Edge[i][k]), &(gm->Edge[i][k+1]), sizeof(int) * (gm->NumVertices-1-k));
      gm->Edge[i][gm->NumVertices - 1] = 0;
    }
    //把每一行向上移动一行
    for(int i = k; i < gm->NumVertices - 1; ++i){
      memmove(gm->Edge[i], gm->Edge[i+1], sizeof(int) * (gm->NumVertices-1));
    }
    memset(gm->Edge[gm->NumVertices - 1], 0, sizeof(int) * (gm->NumVertices - 1));
    //memmove(&(gm->Edge[k]), &(gm->Edge[k+1]), sizeof(int*) * (gm->NumVertices-1-k));
    //memset(gm->Edge[gm->NumVertices - 1], 0, sizeof(int) * (gm->NumVertices - 1));

    //删除点
    memmove(&(gm->VerticesList[k]), &(gm->VerticesList[k+1]), sizeof(T) * (gm->NumVertices-1-k));
  }
  //如果要删除的顶点是最后一个顶点
  else{
    for(int i = 0; i < gm->NumVertices; ++i){
      gm->Edge[i][k] = gm->Edge[k][i] = 0;
    }
  }

  //节点数目减1
  gm->NumVertices--;
}

//摧毁图
void destroy_graph(GraphMtx* gm){
  free(gm->VerticesList);
  for(int i = 0; i < gm->NumVertices; ++i){
    free(gm->Edge[i]);
  }
  free(gm->Edge);
  gm->Edge = NULL;
  gm->VerticesList = NULL;
  gm->MaxVertices = gm->NumVertices = gm->NumEdges = 0;
}

//取得与某顶点有连线的第一个顶点
int getNeighbor(GraphMtx* gm, T v){
  int p = getVertexIndex(gm, v);
  if(-1 == p)return -1;
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->Edge[p][i] == 1)
      return i;
  }
  return -1;
}

//取得与v1顶点，v1顶点之后的v2顶点的之后的有连线的第一个顶点
int getNextNeighbor(GraphMtx* gm, T v1, T v2){
  if(v1 == v2)return -1;
  int p1 = getVertexIndex(gm, v1);
  int p2 = getVertexIndex(gm, v2);
  if(p1 == -1 || p2 == -1)return -1;

  for(int i = p2 + 1; i < gm->NumVertices; ++i){
    if(gm->Edge[p1][i] == 1)
      return i;
  }

  return -1;
}

//取得2个顶点间的权重
E getWeight(GraphMtx* g, int i1, int i2){
  if(i1 == -1 || i2 == -1)
    return MAX_COST;
  else
    return g->Edge[i1][i2];
}
//用prim算法作成最小树
void minSpanTree_prim(GraphMtx* g, T v){
  int n = g->NumVertices;
  E* lowcost = (E*)malloc(sizeof(E) * n);
  int* mst = (int*)malloc(sizeof(int) * n);
  assert(lowcost != NULL && mst != NULL);

  int k = getVertexIndex(g, v);

  for(int i = 0; i < n; ++i){
    if(i != k){
      lowcost[i] = getWeight(g, k, i);
      mst[i] = k;
    }
    else{
      lowcost[i] = 0;
    }
  }

  int min, min_index;
  int begin, end;
  E cost;
  for(int i = 0; i < n - 1; ++i){
    min = MAX_COST;
    min_index = -1;
    for(int j = 0; j < n; ++j){
      if(lowcost[j] != 0 && lowcost[j] < min){
    min = lowcost[j];
    min_index = j;
      }
    }
    begin = mst[min_index];
    end = min_index;
    printf("%c->%c:%d\n",g->VerticesList[begin],g->VerticesList[end],min);

    lowcost[min_index] = 0;

    for(int j = 0; j < n; ++j){
      cost = getWeight(g, min_index, j);
      if(cost < lowcost[j]){
    lowcost[j] = cost;
    mst[j] = min_index;
      }
    }
  }

}

mixSpanTreemain.c

#include "mixSpanTree.h"

int main(){
  GraphMtx gm;
  //初始化图
  init_graph(&gm);
  //插入顶点
  insert_vertex(&gm, ‘A‘);
  insert_vertex(&gm, ‘B‘);
  insert_vertex(&gm, ‘C‘);
  insert_vertex(&gm, ‘D‘);
  insert_vertex(&gm, ‘E‘);
  insert_vertex(&gm, ‘F‘);

  //添加连线
  insert_edge(&gm, ‘A‘, ‘B‘, 6);
  insert_edge(&gm, ‘A‘, ‘D‘, 5);
  insert_edge(&gm, ‘A‘, ‘C‘, 1);
  insert_edge(&gm, ‘B‘, ‘E‘, 3);
  insert_edge(&gm, ‘B‘, ‘C‘, 5);
  insert_edge(&gm, ‘C‘, ‘E‘, 6);
  insert_edge(&gm, ‘C‘, ‘D‘, 5);
  insert_edge(&gm, ‘C‘, ‘F‘, 4);
  insert_edge(&gm, ‘F‘, ‘E‘, 6);
  insert_edge(&gm, ‘D‘, ‘F‘, 2);
  //打印图
  show_graph(&gm);

  //prim
  minSpanTree_prim(&gm, ‘E‘);

  //摧毁图
  destroy_graph(&gm);

}

完整代码
编译方法： gcc -g mixSpanTree.c mixSpanTreemain.c

c/c++ 用普利姆（prim）算法构造最小生成树

标签：连通   图片   经济   --   不能   prim   最小生成树   move   turn   

原文地址：https://www.cnblogs.com/xiaoshiwang/p/9418632.html