标签:努力 完成 冒泡排序 art 表示 out int 将不 image
一.快速排序法
快速排序法建立在冒泡排序之上,对其进行了优化处理。同冒泡排序法,快速排序也是交换元素的位置。冒泡排序法每次将一个元素冒泡在数列的一端,因此效率过慢,其时间复杂度O(n^2)。
快速排序法原理为:采取了递归了思想,选取一个基点元素,每一轮排序将小于/大于基点数值的数放在基点位置左边,将大于/小于基点数值的数放在基点元素右边。每一轮后,基点的位置将不会
改变。利用分割思想,将基点两边的元素看作两个子数列,再次进行排序,直到排序完成。 原理图如下
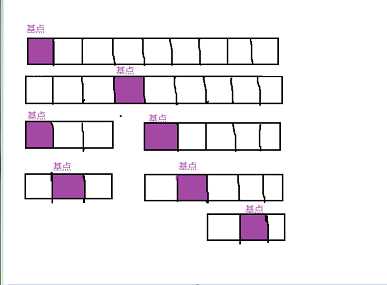
二.代码分析于实现
代码分析:将数列开始元素作为基点元素pivot,用index表示基点位置,用left和right作为遍历指针元素,将数列按照从小到大排序。从指针right开始,把指针指向的元素与基点元素比较,如果
比pivot大,则指针左移;如果比pivot小,则把right指向元素填入index位置中。同理,left指针指向的元素小于pivot则left指针向右移动,如果left指针指向的元素大于pivot,则将left指向元素填入
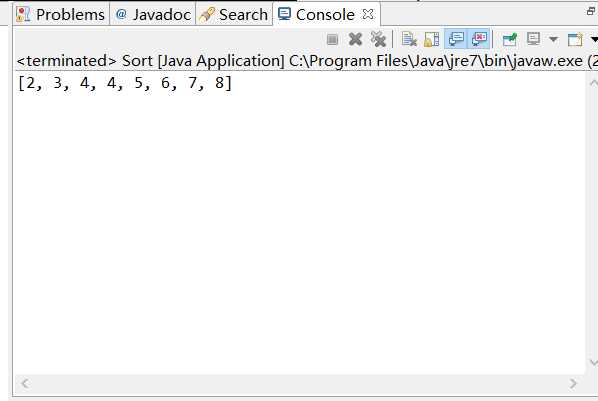
index位置中。最后left与right将会重合,此时index位置的元素将是最后一个需要交换位置的数值的值,将index位置的数值重新赋值为pivotover代码实现:
import java.util.Arrays; public class Sort { public static void main(String arg[]){ int[] arr={4,7,6,3,2,8,4,5}; quickSort(arr, 0, arr.length-1); System.out.println(Arrays.toString(arr)); } public static void quickSort(int[] arr ,int start_number,int end_number) { if(start_number>=end_number) { return ; } int pivot_index=partition(arr,start_number,end_number); quickSort(arr, start_number, pivot_index-1); quickSort(arr, pivot_index+1, end_number);//-1 & +1分割数列 } private static int partition(int[] arr,int start_number,int end_number) { int pivot=arr[start_number]; int left=start_number; int right=end_number; int index=start_number; while(right>=left){ while(right>=left){ if(arr[right]<pivot){ arr[left]=arr[right]; index=right; left++; break; } right--; } while(right>=left){ if(arr[left]>pivot){ arr[right]=arr[left]; index=left; right--; break; } left++; } } arr[index]=pivot; return index; } }
 \
\
三.总结
快速排序法的时间复杂度时多大呢?值得思考,它是随着数列元素初始排布的不同改变呢,还是不变?当然它是前者。
-----------------------趁年轻,多努力------------------------------
标签:努力 完成 冒泡排序 art 表示 out int 将不 image
原文地址:https://www.cnblogs.com/kenhacker-kan/p/9435096.html