标签:png bit 应用 出租车 div random strong int 欧几里得
1、余弦距离:
描述:余弦夹角也可以叫余弦相似度。几何中夹角余弦可用来衡量两个向量方向的差异,机 器学习中借用这一概念来衡量向量样本之间的差异。余弦的取值范围[-1,1],求的两个向量 的夹角并得出夹角对应的余弦值,次余弦值就可以用来表征这两个向量的相似性。夹角越小, 趋近于零度,余弦值越接近于 1,方向也就更吻合。反之,夹角越大,余弦值越接近于-1.特 别的:余弦值为 0 两向量垂直。可以看出,余弦相似度只与方向有关。
公式:
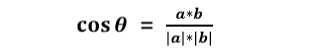
在二维空间中向量 A(x1,y1),B(x2,y2)的夹角余弦公式为:
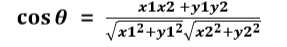
程序实现:
1 import numpy as np 2 from scipy.spatial.distance import pdist 3 from numpy import * 4 5 # 余弦距离 6 def cosDistance(): 7 vec1 = [1,2,3,4] 8 vec2 = [5,6,7,8] 9 10 print("vec1 = ",vec1) 11 print("vec2 = ",vec2) 12 13 # 方法一:根据公式 14 dist1 = np.dot(vec1,vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2)) 15 print ("余弦测试结果 dist1 = "+str(dist1)) 16 17 #方法二:根据scipy库求解 18 Vec = np.vstack([vec1,vec2]) 19 dist2 = 1 - pdist(Vec,‘cosine‘) 20 print("余弦测试结果 dist2 = "+str(dist2))
2、欧氏距离:
描述:欧里几得距离或欧几里得度量是空间两个点的直线距离。较早的文献称毕达哥拉斯度 量。
公式:
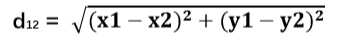
推倒到n维向量:
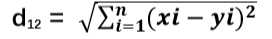
程序实现:
1 import numpy as np 2 from scipy.spatial.distance import pdist 3 from numpy import * 4 # 欧几里得距离 5 def oljdDistance(): 6 vec1 = np.mat([1,2,3,4]) 7 vec2 = np.mat([5,6,7,8]) 8 9 print("vec1 = ",vec1) 10 print("vec2 = ",vec2) 11 12 #方法一 公式求解 13 dist1 = np.sqrt(np.sum(np.square(vec1 - vec2))) 14 print("欧氏距离测试的结果为 dist1 = "+str(dist1)) 15 16 #方法二 根据scipy库求解 17 Vec = np.vstack([vec1,vec2]) 18 dist2 = pdist(Vec) 19 print("欧氏距离测试的结果为 dist2 = "+str(dist2)) 20 21 #方法三 根据公式求解 22 dist3 = sqrt((vec1 - vec2) * (vec1 - vec2).T) 23 print("欧氏距离测试的结果为 dist3 = "+str(dist3))
3、曼哈顿距离:
描述:出租车几何或曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基 所创词汇 ,是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝 对轴距总和。
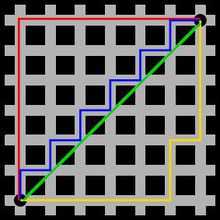
红色:曼哈顿距离
绿色:欧氏距离
公式:
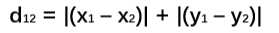
推广到 n 维向量
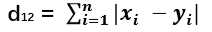
程序实现:
1 import numpy as np 2 from scipy.spatial.distance import pdist 3 from numpy import * 4 # 曼哈顿距离 5 def citybolckDistance(): 6 vec1 = np.mat([1,2,3,4]) 7 vec2 = np.mat([5,6,7,8]) 8 9 print("vec1 = ",vec1) 10 print("vec2 = ",vec2) 11 12 #方法一 根据公式求解 13 dist1 = np.sum(np.abs(vec1 - vec2)) 14 print("曼哈顿距离测试的结果为 dist1 = "+str(dist1)) 15 16 #方法二 根据scipy库求解 17 Vec = np.vstack([vec1,vec2]) 18 dist2 = pdist(Vec,‘cityblock‘) 19 print("曼哈顿距离测试的结果为 dist1 = "+str(dist2)) 20 21 # 方法三 根据公式 22 dist3 = sum(abs(vec1 - vec2)) 23 print("曼哈顿距离测试的结果为 dist1 = "+str(dist3))
4、明可夫斯基距离:
描述:明氏距离又叫做明可夫斯基距离,是欧氏空间中的一种测度,被看做欧氏距离和曼哈 顿距离的一种推广。
公式化: 两个 n 维向量 a(x1,x2,…,xn) 与 b(y1y2,…,yn) 之间的曼哈顿距离
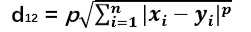
也可写成:
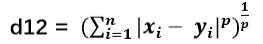
根据变参数的不同,明可夫斯基距离可以表示一类的距离:
1. 当 p = 1 时,就是曼哈顿距离
2. 当 p = 2 时,就是欧氏距离
3. 当 p ->∞时,就是切比雪夫距
程序实现:
import numpy as np from scipy.spatial.distance import pdist from numpy import * # 明可夫斯基距离 def minkowskiDistance(): vec1 = np.mat([1,2,3,4]) vec2 = np.mat([5,6,7,8]) print("vec1 = ",vec1) print("vec2 = ",vec2) #方法一 用scipy库求解 Vec = np.vstack([vec1,vec2]) dist2 = pdist(Vec,‘minkowski‘,p = 1) print("p = 1时scipy库求解曼哈顿距离,结果是:\t"+str(dist2)) #方法二 根据公式求解 dist1 = np.sqrt(np.sum(np.square(vec1 - vec2))) print("平= 2 求解欧氏距离,结果是:\t"+str(dist1)) #方法三 根据公式求解 p = 1 dist3 = sum(abs(vec1 - vec2)) print("p = 1 公式求解曼哈顿距离,结果是:\t"+str(dist3)) #方法四 根据公式求解 p = 2 dist4 = sqrt((vec1 - vec2) * (vec1 - vec2).T) print("p = 2 公式求解欧氏距离,结果是:\t"+str(dist4))
5、切比雪夫距离:
描述:在数学中,切比雪夫距离(Chebyshev distance)或是 L∞度量,是向量空间中的一种 度量,二个点之间的距离定义是其各坐标数值差绝对值的最大值
如图:

国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可 以往斜前或斜后方向移动一格,因此可以较有效率的到达目的的格子。上图是棋盘上所有位置距 f6 位置的 切比雪夫距离。
公式化: 二维平面两点 a(x1,y1) b(x2,y2)之间的切比雪夫距离
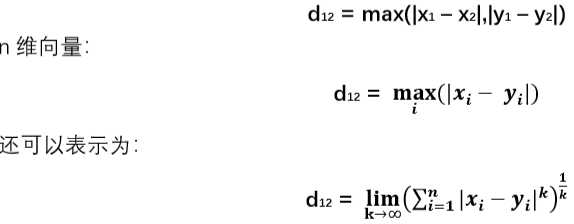
程序实现:
1 import numpy as np 2 from scipy.spatial.distance import pdist 3 from numpy import * 4 # 切比雪夫距离 5 def chebyshevDistance(): 6 vec1 = np.mat([1,2,3,4]) 7 vec2 = np.mat([5,6,7,8]) 8 9 print("vec1 = ",vec1) 10 print("vec2 = ",vec2) 11 12 #方法一 根据公式求解 13 dist1 = np.max(np.abs(vec1 - vec2)) 14 print("公式求解切比雪夫距离:\t"+str(dist1)) 15 16 #方法二 根据scipy库求解 17 Vec = np.vstack([vec1,vec2]) 18 dist2 = pdist(Vec,‘chebyshev‘) 19 print("scipy库求解切比雪夫距离:\t"+str(dist2))
6、杰卡德距离:
描述: 1. 杰卡德相似系数:两个集合 A 和 B 的交集元素在 A、B 并集中所占的比例,称为两个集 合的杰卡德相似系数,用符号 J(A,B)表示。
2. 杰卡德距离:与杰卡德系数相反的概念,用两个集合中不同元素占所有元素的比例来衡 量两个集合的区分度,这就是杰卡德距离。
其应用:杰卡德相似系数用在衡量样本相似度上。
公式化:
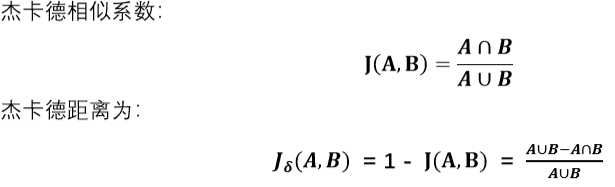
程序实现:
1 import numpy as np 2 from scipy.spatial.distance import pdist 3 from numpy import * 4 #杰卡德距离 5 def jaccardDistance(): 6 v1 = np.random.random(10) > 0.5 7 v2 = np.random.random(10) > 0.5 8 9 vec1 = np.asarray(v1,np.int32) 10 vec2 = np.asarray(v2,np.int32) 11 12 print("vec1 = ",vec1) 13 print("vec2 = ",vec2) 14 15 #方法一 根据公式求解 16 up = np.double(np.bitwise_and((vec1 != vec2),np.bitwise_or(vec1 != 0,vec2 != 0)).sum()) 17 down = np.double(np.bitwise_or(vec1 != 0,vec2 != 0).sum()) 18 dist1 = (up / down) 19 print("公式求解杰卡德距离:\t"+str(dist1)) 20 21 #方法二 根据scipy库求解 22 Vec = np.vstack([vec1,vec2]) 23 dist2 = pdist(Vec,‘jaccard‘) 24 print("scipy求解杰卡德距离:\t"+str(dist2))
7、汉明距离
描述:在信息论中两个等长字符串之间的距离是两个字符串对应位置的不同字符的个数。换 句话说,也就是将一个字符串换成另一个字符串所需要替换的字符个数。
公式化描述: 1011101 与 1001001 之间的汉明距离是 2
程序实现:
1 import numpy as np 2 from scipy.spatial.distance import pdist 3 from numpy import * 4 #汉明距离 5 def hammingDistance(): 6 v1 = np.random.random(10)>0.5 7 v2 = np.random.random(10)>0.5 8 9 vec1 = np.asarray(v1,np.int32) 10 vec2 = np.asarray(v2,np.int32) 11 12 print("vec1 = ",vec1) 13 print("vec2 = ",vec2) 14 15 #方法一 根据公式求解 16 dist1 = np.mean(vec1!=vec2) 17 print("公式求解汉明距离为:\t"+str(dist1)) 18 19 #方法二 根据scipy库求解 20 Vec = np.vstack([vec1,vec2]) 21 dist2 = pdist(Vec,‘hamming‘) 22 print("scipy库求解汉明距离:\t"+str(dist2))
标签:png bit 应用 出租车 div random strong int 欧几里得
原文地址:https://www.cnblogs.com/IamJiangXiaoKun/p/9463004.html