标签:clu 入口 染色体 htm 空间复杂度 ali 技术 const 矩阵
浅谈遗传算法:https://www.cnblogs.com/AKMer/p/9479890.html
\(mzf\)在踏上寻找\(oxy\)的路程之后不小心碰到了大魔王\(fater\)。
大魔王看了看\(mzf\)的命运,心生怜悯,便给\(mzf\)和自己做一个交换的机会。
这个交换是这样的:
由于\(oxy\)不知在天涯海角,\(mzf\)的要找到实在是太难了。所以大魔王愿意把\(mzf\)和\(oxy\)同时扔到一个迷宫(\(n\)个点的完全无向图)里,但是\(oxy\)在哪个点上是未知的。
\(mzf\)初始在\(1\)号点。\(1\)号点上有迷宫出口,打开出口需要遍历整张图拿到全部点上的钥匙。\(mzf\)要将自己日思夜念的\(oxy\)从迷宫深处的不知方位的点带出来就必须遍历所有的点。然而大魔王并不愿意一昧的帮助\(mzf\),他说如果\(mzf\)重复经过一个点或者走过的路程不是最短的环那么他和\(oxy\)将永远无法逃出迷宫。
\(mzf\)想见\(oxy\),不管三七二十一便答应了大魔王。在进去之前大魔王给了他一张地图,然后便将\(mzf\)扔进了迷宫并且关上了入口。
\(mzf\)在黑暗的迷宫里才明白过来,自己虽然是\(OIer\),但是自己的\(Computer\)似乎被大魔王没收了。于是乎,作为同是\(OIer\)的挚友,他打电话告诉你这件事情并且希望你能帮助他。他将地图以一个矩阵的形式给了你。由于他实在是太想念\(oxy\)了,但他也不好意思太麻烦你,所以他希望你能在\(1s\)内帮他算出最短路径。只要你告诉他正确的答案,出题人就会告诉他怎么走才是最优的。
输入一共\(n+1\)行
第一行一个数字\(n\)
接下来一个\(n\)阶矩阵,\(dis[i][j]\)记录\(i,j\)之间的距离
输出仅一行
一个数字表示最短的哈密尔顿环的长度
4
0 1 2 3
1 0 2 3
2 2 0 3
3 3 3 0
9
\(n\leqslant100,dis[i][j]\leqslant100000\)
我自己造的数据:https://files.cnblogs.com/files/AKMer/TSP.zip
由于爆搜跑得慢所以只造了\(n\leqslant12\)的数据
首先题目意思是要你求一个无向完全图中最短哈密尔顿环的长度。
对于这题用遗传算法,估价函数可以设成一个最长环长度减去当前染色体所表示的环的长度,那么环长度越短,适应性就会越高。
然后交换操作要进行一些改进。因为直接交换会使得某个染色体中重复出现某个点(会导致\(mzf\)和\(oxy\)不能逃出迷宫!!)。于是乎我们就将串与串之间交换改成在一条染色体上交换两个位置,和变异一起做了。
就大功告成了。如果是提答题的话遗传代数和变异次数可以设置多一点,如果是想在传统题上骗分记得不要设置太高导致\(TLE\)。
一开始\(srand(time(0))\)狂\(Wa\)不止:
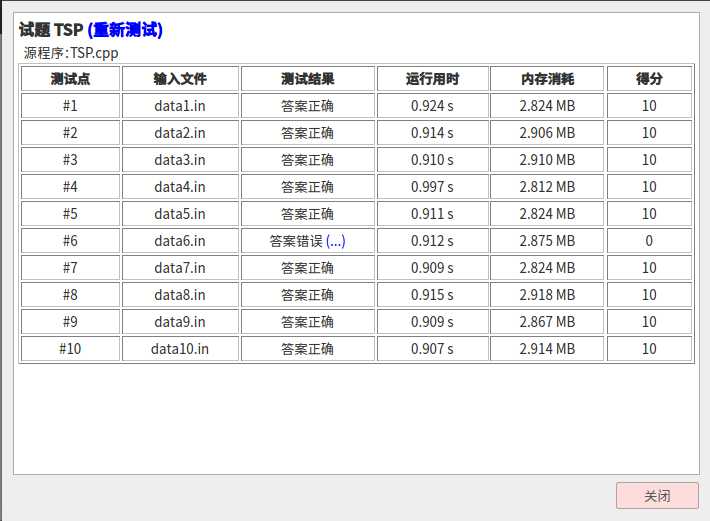
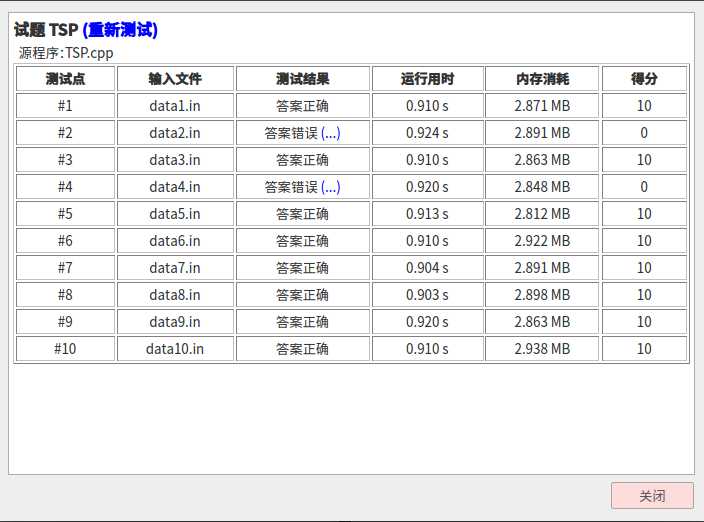
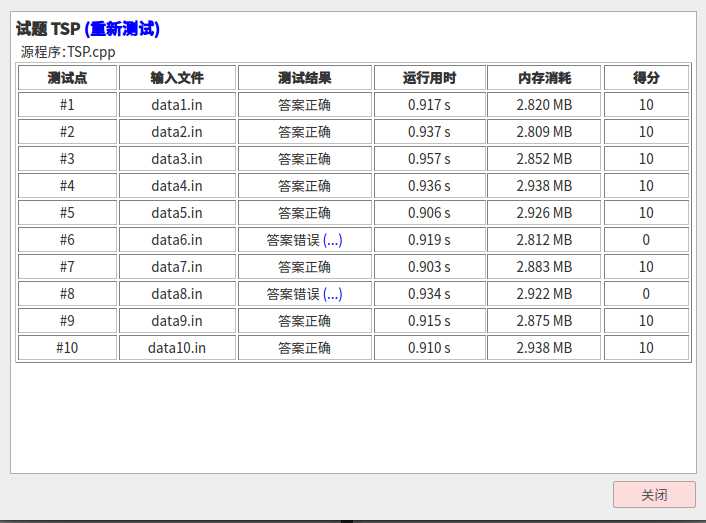
难道就只能这样了吗?不!
后来我\(srand\)我俩的名字首字母就\(A\)掉了哈哈哈
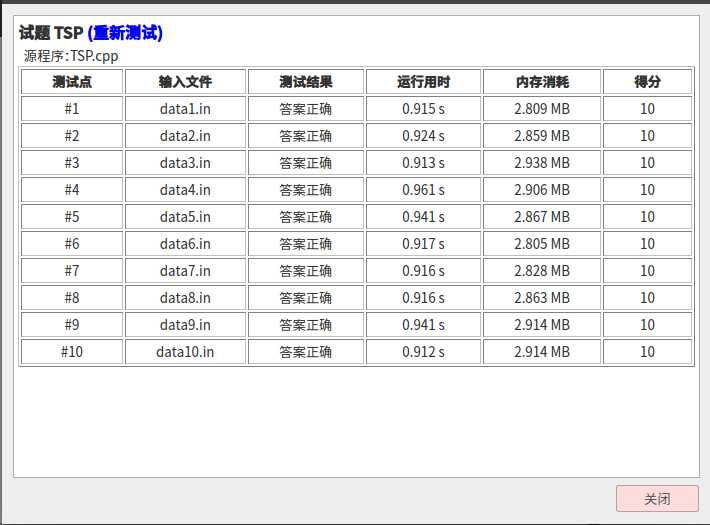
时间复杂度:\(O(欧洲人)\)
空间复杂度:\(O(n)\)
代码如下:
#include <ctime>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int inf=10000005;
const int maxn=105;
int dis[maxn][maxn];//dis存距离
int f[maxn],f1[maxn],g[maxn];//f存适应度函数,f1缓存f,g存确定性选择法下选几次
int n,low=inf,mx_f,tim,chr_cnt=100;//low存当前种群中最短长度,tim存low持续不变了多少代,chr_cnt存染色体条数,mx_f存当前种群最长环长度
int read() {
int x=0,f=1;char ch=getchar();
for(;ch<‘0‘||ch>‘9‘;ch=getchar())if(ch==‘-‘)f=-1;
for(;ch>=‘0‘&&ch<=‘9‘;ch=getchar())x=x*10+ch-‘0‘;
return x*f;
}//快读
int random(int limit) {
return rand()%limit;
}//rand一个[0,limit)范围的数字
struct Chromosome {
int gene[maxn];//存环上点的顺序
int calc() {
int res=0;
for(int i=2;i<=n;i++)
res+=dis[gene[i-1]][gene[i]];
return res+dis[gene[n]][gene[1]];//依次累加环上的边
}//算适应度函数
void Initialization() {
for(int i=1;i<=n;i++)
gene[i]=i;
random_shuffle(gene+1,gene+n+1);
}//初始化
}chr[maxn],new_chr[maxn],ans;//chr存当前种群,new_chr存下一代种群,ans存方案,最后用于统计答案
void select() {//选择
for(int i=1;i<=chr_cnt;i++) {
f[i]=chr[i].calc();//算最短路
mx_f=max(mx_f,f[i]);
if(f[i]<low) {
low=f[i],tim=0;
ans=chr[i];//如果更新low就更新全局答案
}
}
tim++;int res=0,cnt=0;//res存总适应度,cnt存下一代染色体条数
for(int i=1;i<=chr_cnt;i++)
f[i]=mx_f-f[i]+1,res+=f[i];//更新适应度,累加到res里
for(int i=1;i<=chr_cnt;i++)
g[i]=1.0*f[i]/res*chr_cnt,f1[i]=f[i],cnt+=g[i];//算g[i],将f缓存到f1里
while(cnt<chr_cnt)g[random(chr_cnt)+1]++,cnt++;//没有选满就继续选
cnt=0;
for(int i=1;i<=chr_cnt;i++) {
for(int j=1;j<=g[i];j++) {
new_chr[++cnt]=chr[i];
f[cnt]=f1[i];//同步更新适应度
if(cnt==chr_cnt)break;
}
if(cnt==chr_cnt)break;//满了就不加了
}//模拟选择过程
for(int i=1;i<=chr_cnt;i++)
chr[i]=new_chr[i];//更新chr
}
void variety() {//变异
for(int i=1;i<=500*chr_cnt;i++) {//不用交换的话就多变异几次
int u=random(chr_cnt)+1,l=random(n)+1,r=random(n)+1;//u是即将变异的染色体,l和r是要交换的位置
Chromosome tmp=chr[u];swap(tmp.gene[l],tmp.gene[r]);
int res=tmp.calc();//tmp缓存变异后的染色体
if(res<chr[u].calc()) {//如果编译后更优了就变异
chr[u]=tmp;
f[u]=mx_f-res;//更新染色体和适应度
}
}
}
void Genetic() {
while(1) {
select();
if(tim>200)return;//超过200代不变就算正确了
variety();
}//遗传过程
}
int main() {
srand(‘o‘+‘x‘+‘y‘+‘m‘+‘z‘+‘f‘);//她叫oxy,我是mzf
n=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=read();//读入
for(int i=1;i<=chr_cnt;i++)
chr[i].Initialization();//初始化祖先种群
Genetic();//遗传
printf("%d\n",ans.calc());//输出
return 0;
}标签:clu 入口 染色体 htm 空间复杂度 ali 技术 const 矩阵
原文地址:https://www.cnblogs.com/AKMer/p/9496777.html