标签:ima 就是 machine alt 分离 识别 分类 不可 模式识别
不同时期的你去看红楼梦会有不一样的感触,而不同年份的我看ML也会有更深入的理解(*/ω\*)
svm是 一种判别方法 有监督的学习模型 通常用来进行模式识别、分类以及回归分析,主要解决二分类问题。其原理也从线性可分说起,然后扩展到线性不可分的情况。甚至扩展到使用非线性函数中去。
所以,我们先从最简单的线性支持向量机说起。
去年翻ML时,仍不解svm为什么叫支持向量机.或许 同时翻翻线性回归和线性支持向量机就能豁然开朗。
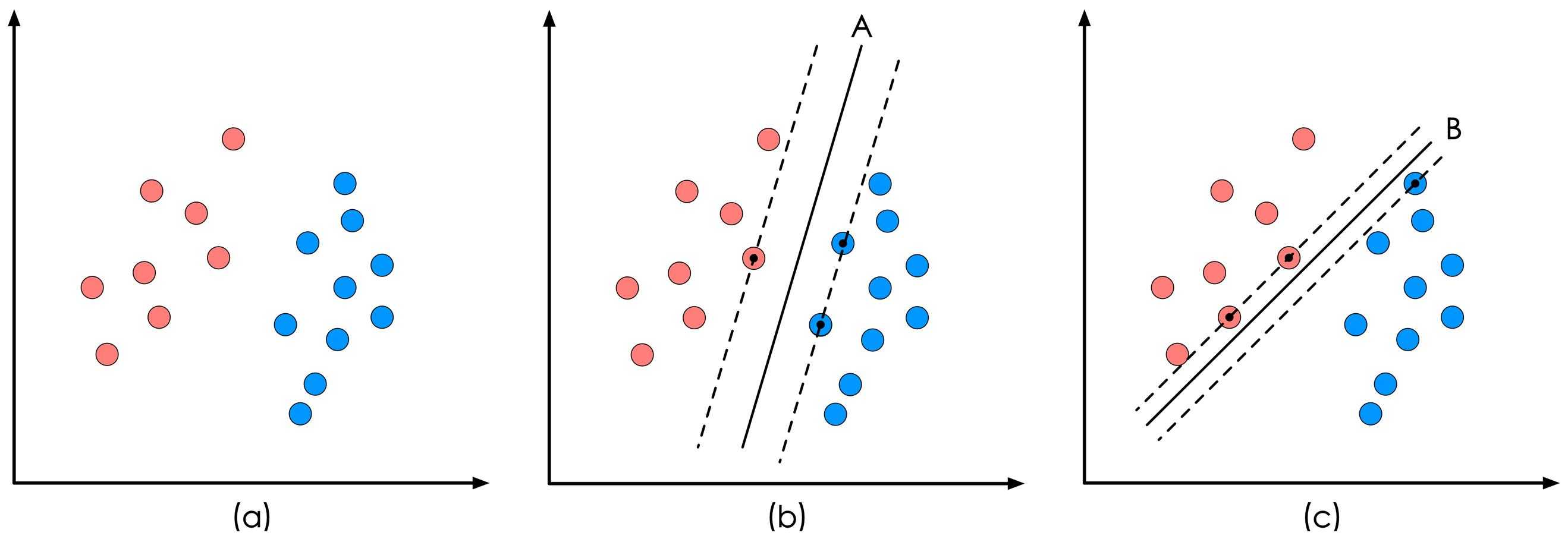
如果一个线性函数能够将样本分开,称这些数据样本是线性可分的。那么什么是线性函数呢?其实很简单,在二维空间中就 是一条直线,在三维空间中就是一个平面,以此类推,如果不考虑空间维数,这样的线性函数统称为超平面。我们看一个简单的二维空间的例子,
样本是线性可分的,但是很显然不只有这一条直线可以将样本分开,而是有无数条,我们所说的线性可分支持向量机就对应 着能将数据正确划分并且间隔最大的直线。
线性回归,通常采用最小二乘法作为损失函数,即实际值与观测值相减的平方和最小作为其选取直线的标准。
线性支持向量机,主要思想是:寻找这么一条直线,使得训练样本中属于不同类别的样本点正好位于该直线的两侧,在保证 分类精度的同时,使得直线两侧的空白区域最大化。
为什么要间隔最大呢?一般来说,一个点距离分离超平面的远近可以表示分类预测的确信度,如图中的A B两个样本点,B点 被预测为正类的确信度要大于A点,所以SVM的目标是寻找一个超平面,使得离超平面较近的异类点之间能有更大的间隔,即 不必考虑所有样本点,只需让求得的超平面使得离它近的点(“支持向量”)间隔最大(svm名称的由来?)。 故而SVM自带结构 风险最小化,LR(线性回归Linear Regress)则是经验风险最小化
图5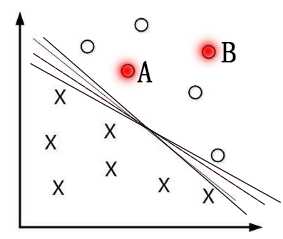
那么怎么计算间隔?
松弛变量
SVM另一个巧妙之处是加入了一个松弛变量来处理样本数据可能存在的噪声问题,如下图所示:
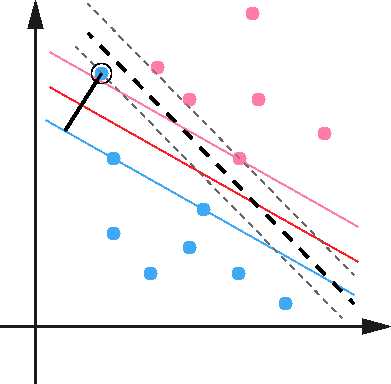
SVM允许数据点在一定程度上对超平面有所偏离,这个偏移量就是SVM算法中可以设置的outlier值,对应于上图中黑色实现的 长度。松弛变量的加入使得SVM并非仅仅是追求局部效果最优,而是从样本数据分布的全局出发,统筹考量,正所谓成大事者 不拘小节。
支持向量机 SVM (Support Vector Machine)
标签:ima 就是 machine alt 分离 识别 分类 不可 模式识别
原文地址:https://www.cnblogs.com/Zhouwl/p/9519855.html