标签:工作原理 targe lang order baidu false for star 顺序
百度百科:归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并操作:
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11;
逆序数为14
图例:
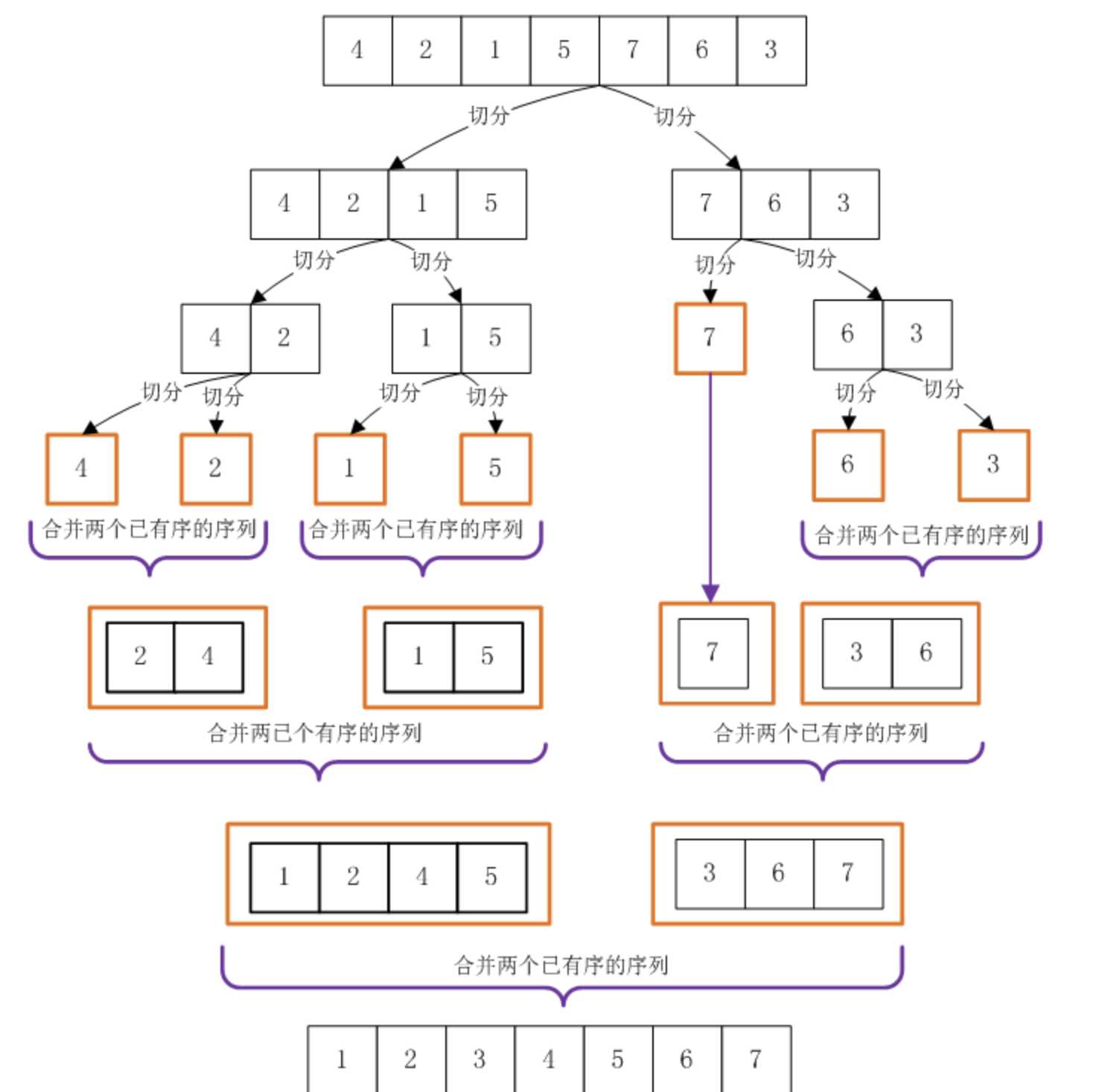
java代码实现:
package com.newtouch.data.sort; import com.newtouch.data.test.SortTestHelper; import java.util.Arrays; /** * 归并排序的算法实现 * 实现复杂度o */ public class MergeSort { //算法类不允许产生任何实例 private MergeSort() { } //将arr[l...mid] 和arr[mid+1....r] 两部分进行归并 private static void merge(Comparable[] arr, int l, int mid, int r) { Comparable[] aux = Arrays.copyOfRange(arr, l, r + 1); //初始化,i指向左半部分的起始;j指向右半部分其实索引位置mid+1 int i = l, j = mid + 1; for (int k = l; k <= r; k++) { // if (i > mid) { //左半部分元素已经全部处理完毕 arr[k] = aux[j - l]; j++; } else if (j > r) { //右半部分元素已经全部处理完毕 arr[k] = aux[i - l]; i++; } else if (aux[i - l].compareTo(aux[j - i]) < 0) { //左半部分所指元素<右半部分所指元素 arr[k] = aux[i - l]; i++; } else { arr[k] = aux[j - l]; j++; } } } private static void sort(Comparable[] arr, int l, int r) { if (l >= r) return; int mid = (r + l) / 2; sort(arr, l, mid); sort(arr, mid + 1, r); merge(arr, l, mid, r); } public static void sort(Comparable[] arr) { int n = arr.length; sort(arr, 0, n - 1); } public static void main(String[] args) { // Merge Sort是我们学习的第一个O(nlogn)复杂度的算法 // 可以在1秒之内轻松处理100万数量级的数据 // 注意:不要轻易尝试使用SelectionSort, InsertionSort或者BubbleSort处理100万级的数据 // 否则,你就见识了O(n^2)的算法和O(nlogn)算法的本质差异:) int N = 1000000; Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000); SortTestHelper.testSort("com.newtouch.data.sort.MergeSort", arr); return; } }
测试辅助工具类实现:
package com.newtouch.data.test; import java.lang.reflect.Method; import java.lang.Class; import java.util.Random; public class SortTestHelper { // SortTestHelper不允许产生任何实例 private SortTestHelper() { } // 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR] public static Integer[] generateRandomArray(int n, int rangeL, int rangeR) { assert rangeL <= rangeR; Integer[] arr = new Integer[n]; for (int i = 0; i < n; i++) arr[i] = new Integer((int) (Math.random() * (rangeR - rangeL + 1) + rangeL)); return arr; } // 生成一个近乎有序的数组 // 首先生成一个含有[0...n-1]的完全有序数组, 之后随机交换swapTimes对数据 // swapTimes定义了数组的无序程度: // swapTimes == 0 时, 数组完全有序 // swapTimes 越大, 数组越趋向于无序 public static Integer[] generateNearlyOrderedArray(int n, int swapTimes) { Integer[] arr = new Integer[n]; for (int i = 0; i < n; i++) arr[i] = new Integer(i); for (int i = 0; i < swapTimes; i++) { int a = (int) (Math.random() * n); int b = (int) (Math.random() * n); int t = arr[a]; arr[a] = arr[b]; arr[b] = t; } return arr; } // 打印arr数组的所有内容 public static void printArray(Object[] arr) { for (int i = 0; i < arr.length; i++) { System.out.print(arr[i]); System.out.print(‘ ‘); } System.out.println(); return; } // 判断arr数组是否有序 public static boolean isSorted(Comparable[] arr) { for (int i = 0; i < arr.length - 1; i++) if (arr[i].compareTo(arr[i + 1]) > 0) return false; return true; } // 测试sortClassName所对应的排序算法排序arr数组所得到结果的正确性和算法运行时间 public static void testSort(String sortClassName, Comparable[] arr) { // 通过Java的反射机制,通过排序的类名,运行排序函数 try { // 通过sortClassName获得排序函数的Class对象 Class sortClass = Class.forName(sortClassName); // 通过排序函数的Class对象获得排序方法 Method sortMethod = sortClass.getMethod("sort", new Class[]{Comparable[].class}); // 排序参数只有一个,是可比较数组arr Object[] params = new Object[]{arr}; long startTime = System.currentTimeMillis(); // 调用排序函数 sortMethod.invoke(null, params); long endTime = System.currentTimeMillis(); assert isSorted(arr); System.out.println(sortClass.getSimpleName() + " : " + (endTime - startTime) + "ms"); } catch (Exception e) { e.printStackTrace(); } } }
测试结果:MergeSort : 447ms 100万数据在0.5内就完成类排序。
标签:工作原理 targe lang order baidu false for star 顺序
原文地址:https://www.cnblogs.com/caibixiang123/p/9545376.html