标签:dijkstra 表示 png 起点到终点 有向无环图 bubuko tar ESS sse
找出最快的路径使用算法——狄克斯特拉算法(Dijkstra’s algorithm)。
(1) 找出最便宜的节点,即可在最短时间内前往的节点。
(2) 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。
(3) 重复这个过程,直到对图中的每个节点都这样做了。
(4) 计算最终路径。
狄克斯特拉算法用于每条边都有关联数字的图,这些数字称为权重(weight)。
带权重的图称为加权图( weighted graph),不带权重的图称为非加权图(unweighted graph)。
要计算非加权图中的最短路径,可使用广度优先搜索。要计算加权图中的最短路径,可使用狄克斯特拉算法。
可从一个节点出发,走一圈后又回到这个节点。
无向图意味着两个节点彼此指向对方,其实就是环!
狄克斯特拉算法只适用于有向无环图(directed acyclicgraph,DAG)。
不能将狄克斯特拉算法用于包含负权边的图
狄克斯特拉算法这样假设:对于处理过的海报节点,没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。
示例:求起点到终点的最短路径
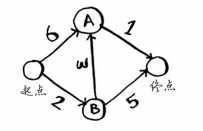
#创建所有节点和路径的散列表
graph={‘start‘: {‘a‘: 6, ‘b‘: 2}, ‘a‘: {‘fin‘: 1}, ‘b‘: {‘a‘: 3, ‘fin‘: 5}, ‘fin‘: {}}
#创建已知节点花销的散列表
costs={‘a‘: 6, ‘b‘: 2, ‘fin‘: float("inf")} #float(‘inf‘) 表示正无穷
#储存父节点的散列表
parents={‘a‘: ‘start‘, ‘b‘: ‘start‘, ‘fin‘: None}
#存储已访问过节点的列表
processed=[]
#定义一个寻找最小花销的函数
def find_lowest_cost_node(costs):
lowest_cost = float("inf")
lowest_cost_node = None
for node in costs: #遍历所有节点
cost = costs[node]
if cost < lowest_cost and node not in processed: #寻找花销最小,且没有访问过的点
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
node = find_lowest_cost_node(costs) #找到花销最小的节点
while node is not None: #这个while循环在所有节点都被处理过后结束
cost = costs[node]
neighbors = graph[node]
for n in neighbors.keys(): #遍历当前节点的所有邻居
new_cost = cost + neighbors[n] #该节点到达该邻居的花销总和
if costs[n] > new_cost: #如果经当前节点前往该邻居更近
costs[n] = new_cost #更新该邻居的花销
parents[n] = node #同时将该邻居的父节点设置为当前节点
processed.append(node) #将当前节点标记为处理过
node = find_lowest_cost_node(costs) #找出接下来要处理的节点,并循环
print(parents)
【算法】狄克斯特拉算法(Dijkstra’s algorithm)
标签:dijkstra 表示 png 起点到终点 有向无环图 bubuko tar ESS sse
原文地址:https://www.cnblogs.com/lilip/p/9547383.html