标签:二叉树的遍历 turn tree node amp scom main 二叉树 com 技术
1. 二叉树的遍历:先序(递归、非递归),中序(递归、非递归),后序(递归、非递归)。
#include <iostream> #include <string> #include <stack> using namespace std; struct BiTree { int NodeData = 0; struct BiTree *pLeft = nullptr; struct BiTree *pRight = nullptr; }; //遍历二叉树: void show(struct BiTree *pRoot, int n) { if (pRoot == nullptr) { return; } else { show(pRoot->pLeft, n + 1); for (int i = 0; i < n; i++) cout << " "; cout << pRoot->NodeData << endl; show(pRoot->pRight, n + 1); } } //-------------------------------------------------------------- //递归中序遍历: void RecMidTravel(struct BiTree *pRoot) { if (pRoot == nullptr) { return; } else { if (pRoot->pLeft != nullptr) { RecMidTravel(pRoot->pLeft); } cout << pRoot->NodeData << endl; if (pRoot->pRight != nullptr) { RecMidTravel(pRoot->pRight); } } } //中序非递归 void MidTravel(struct BiTree *pRoot) { if (pRoot == nullptr) { return; } else { struct BiTree *pcur = pRoot; stack<BiTree *> mystack; while (!mystack.empty() || pcur != nullptr) { while (pcur != nullptr) { mystack.push(pcur); pcur = pcur->pLeft; //左节点全部进栈 } if (!mystack.empty()) { pcur = mystack.top(); cout << pcur->NodeData << endl; mystack.pop(); //出栈 pcur = pcur->pRight; //右节点 } } } } //-------------------------------------------------------------- //递归先序遍历: void RecPreTravel(struct BiTree *pRoot) { if (pRoot == nullptr) { return; } else { cout << pRoot->NodeData << endl; if (pRoot->pLeft != nullptr) { RecPreTravel(pRoot->pLeft); } if (pRoot->pRight != nullptr) { RecPreTravel(pRoot->pRight); } } } //先序非递归 void PreTravel(struct BiTree *pRoot) { if (pRoot == nullptr) { return; } else { struct BiTree *pcur = pRoot; stack<BiTree *> mystack; while (!mystack.empty() || pcur != nullptr) { while (pcur != nullptr) { cout << pcur->NodeData << endl; mystack.push(pcur); pcur = pcur->pLeft; //左节点全部进栈 } if (!mystack.empty()) { pcur = mystack.top(); mystack.pop(); //出栈 pcur = pcur->pRight; //右节点 } } } } //-------------------------------------------------------------- //递归后序遍历: void RecPostTravel(struct BiTree *pRoot) { if (pRoot == nullptr) { return; } else { if (pRoot->pLeft != nullptr) { RecPostTravel(pRoot->pLeft); } if (pRoot->pRight != nullptr) { RecPostTravel(pRoot->pRight); } cout << pRoot->NodeData << endl; } } //后序非递归 struct nosame //标识节点是否反复出现 { struct BiTree *pnode; bool issame; }; void PostTravel(struct BiTree *pRoot) { if (pRoot == nullptr) { return; } else { struct BiTree *pcur = pRoot; stack<nosame *> mystack; //避免重复出现 nosame *ptemp; while (!mystack.empty() || pcur != nullptr) { while (pcur != nullptr) { nosame *ptr = new nosame; ptr->issame = true; ptr->pnode = pcur;//节点 //cout << pcur->NodeData << endl; mystack.push(ptr); pcur = pcur->pLeft; //左节点全部进栈 } if (!mystack.empty()) { ptemp = mystack.top(); mystack.pop(); //出栈 if (ptemp->issame == true) //第一次出现 { ptemp->issame = false; mystack.push(ptemp); pcur = ptemp->pnode->pRight;//跳到右节点 } else { cout << ptemp->pnode->NodeData << endl;//打印数据 pcur = nullptr; } } } } } void main() { struct BiTree *pRoot; struct BiTree node1; struct BiTree node2; struct BiTree node3; struct BiTree node4; struct BiTree node5; struct BiTree node6; struct BiTree node7; struct BiTree node8; node1.NodeData = 1; node2.NodeData = 2; node3.NodeData = 3; node4.NodeData = 4; node5.NodeData = 5; node6.NodeData = 6; node7.NodeData = 7; node8.NodeData = 8; pRoot = &node1; node1.pLeft = &node2; node1.pRight = &node3; node2.pLeft = &node4; node2.pRight = &node5; node3.pLeft = &node6; node3.pRight = &node7; node4.pLeft = &node8; show(pRoot, 1); cout << "中序递归:" << endl; RecMidTravel(pRoot); //中序递归 cout << "中序非递归:" << endl; MidTravel(pRoot); //中序非递归 cout << "先序递归:" << endl; RecPreTravel(pRoot); cout << "先序非递归:" << endl; PreTravel(pRoot); //先序非递归 cout << "后序递归:" << endl; RecPostTravel(pRoot); cout << "后序非递归:" << endl; PostTravel(pRoot); //后序非递归 cin.get(); }

2. 获取二叉树节点个数:
//递归获取二叉树节点个数 int getNodeCount(BiTree *pRoot) { if (pRoot == nullptr) { return 0; } else { return getNodeCount(pRoot->pLeft) + getNodeCount(pRoot->pRight) + 1; } }

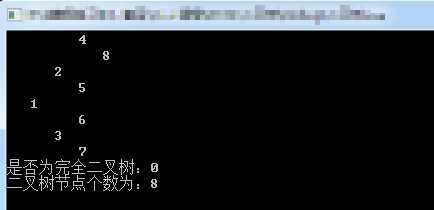
3. 判断二叉树是否为完全二叉树:
//判断二叉树是否为完全二叉树 bool isCompleteBiTree(BiTree *pRoot) { if (pRoot == nullptr) { return false; } else { queue<BiTree *> myq; myq.push(pRoot); bool mustHaveChild = false; //必须有子节点 bool result = true; //结果 while (!myq.empty()) { BiTree *node = myq.front();//头结点 myq.pop(); //出队 if (mustHaveChild) //必须有孩子 { if (node->pLeft != nullptr || node->pRight != nullptr) { result = false; break; } } else { if (node->pLeft != nullptr && node->pRight != nullptr) { myq.push(node->pLeft); myq.push(node->pRight); } else if (node->pLeft != nullptr && node->pRight == nullptr) { mustHaveChild = true; myq.push(node->pLeft); } else if (node->pLeft == nullptr && node->pRight != nullptr) { result = false; break; } else { mustHaveChild = true; } } } return result; } }
4. 求二叉树两个节点的最小公共祖先:
//求二叉树两个节点的最小公共祖先 bool findnode(BiTree *pRoot, BiTree *node) //判断节点是否在某个节点下 { if (pRoot == nullptr || node == nullptr) { return false; } if (pRoot == node) { return true; } bool isfind = findnode(pRoot->pLeft, node); if (!isfind) { isfind = findnode(pRoot->pRight, node); } return isfind; } BiTree *getParent(BiTree *pRoot, BiTree *pChild1, BiTree *pChild2) { if (pRoot == pChild1 || pRoot == pChild2) { return pRoot; } if (findnode(pRoot->pLeft, pChild1)) { if (findnode(pRoot->pRight, pChild2)) { return pRoot; } else { return getParent(pRoot->pLeft, pChild1, pChild2); } } else { if (findnode(pRoot->pLeft, pChild2)) { return pRoot; } else { return getParent(pRoot->pRight, pChild1, pChild2); } } }

5. 二叉树的翻转:
//二叉树的翻转 BiTree *revBiTree(BiTree *pRoot) { if (pRoot==nullptr) { return nullptr; } BiTree *leftp = revBiTree(pRoot->pLeft); BiTree *rightp = revBiTree(pRoot->pRight); pRoot->pLeft = rightp; pRoot->pRight = leftp; //交换 return pRoot; }

6. 求二叉树第k层的节点个数:
//求二叉树第K层的节点个数 int getLevelConut(BiTree *pRoot, int k) { if (pRoot == nullptr || k < 1) { return 0; } if (k == 1) { return 1; } else { int left = getLevelConut(pRoot->pLeft, k - 1); int right = getLevelConut(pRoot->pRight, k - 1); return (left + right); } }

7. 求二叉树中节点的最大距离(相距最远的两个节点之间的距离):
//求二叉树中节点的最大距离 struct res //用以递归间传递距离 { int maxDistance = 0; int maxDepth = 0; }; res getMaxDistance(BiTree *pRoot) { if (pRoot == nullptr) { res r1; return r1; } res leftr = getMaxDistance(pRoot->pLeft); res rightr = getMaxDistance(pRoot->pRight); res last; //最终结果 last.maxDepth = max(leftr.maxDepth + 1, rightr.maxDepth + 1);//求最大深度 last.maxDistance = max(max(leftr.maxDistance, rightr.maxDistance), leftr.maxDepth + rightr.maxDepth + 2);//求最大距离 return last; }

8. 判断二叉树是否为平衡二叉树:
//判断二叉树是否为平衡二叉树: bool isAVL(BiTree *pRoot, int & depth) //需要引用来传递数据 { if (pRoot == nullptr) { depth = 0; return true; } int leftdepth = 0; int rightdepth = 0; bool left = isAVL(pRoot->pLeft, leftdepth); bool right = isAVL(pRoot->pRight, rightdepth); if (left && right && abs(leftdepth - rightdepth) <= 1) { depth = 1 + (leftdepth > rightdepth ? leftdepth : rightdepth);//深度 return true; } else { return false; } }


标签:二叉树的遍历 turn tree node amp scom main 二叉树 com 技术
原文地址:https://www.cnblogs.com/si-lei/p/9547016.html