标签:fft stat 矩阵链 有助于 数论 拓扑排序 傅里叶变换 无限 bellman
1.算法在计算中的作用
1.1算法
算法解决哪些问题
数据结构
技术,算法设计分析技术
难题,PE完全问题
并行性
1.2作为一种技术的算法
效率
算法与其他技术
2.算法基础
2.1插入排序
代码
public static void main(String[] args) { int[] array = {5, 2, 4, 6, 1, 3}; for (int j = 1; j < array.length; j++) { int key = array[j];//从第2个元素开始和前一个元素进行比较 int i = j - 1; while (i > -1 && array[i] > key) {//第n个元素和第n-1个元素开始比较,直到第1个元素, array[i + 1] = array[i];//将找到的元素值给第n个元素 i--; } array[i + 1] = key;//将找到的元素赋值为第n个元素值 } for (int i = 0; i < array.length; i++) { if (i == 0) { System.out.print("[" + array[i]); } else if (i == array.length - 1) { System.out.print("," + array[i] + "]"); } else { System.out.print("," + array[i]); } } }
图示
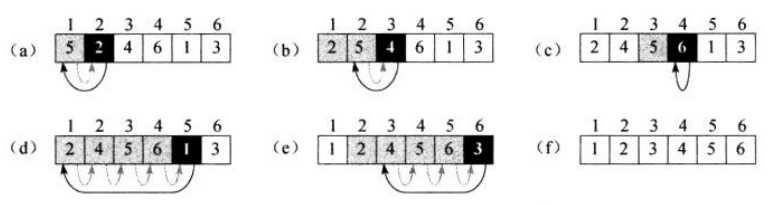
初始化:循环第一次迭代前为真
保持:某次迭代前为真,下次迭代之前仍为真
终止:循环终止时,不变式为我们提供有用的性质,该性质有助于证明算法是正确的
降序
int[] array = {5, 2, 4, 6, 1, 3}; for (int j = array.length - 2; j > -1; j--) { int key = array[j]; int i = j + 1; while (i < array.length && array[i] > key) { array[i - 1] = array[i]; i++; } array[i - 1] = key; }
2.2分析算法
例如求2的5阶乘,可以二进制进行左移5位
2.3设计算法
2.3.1分治法
分解元问题为若干子问题
解决这些子问题
合并这些子问题
归并排序
图示

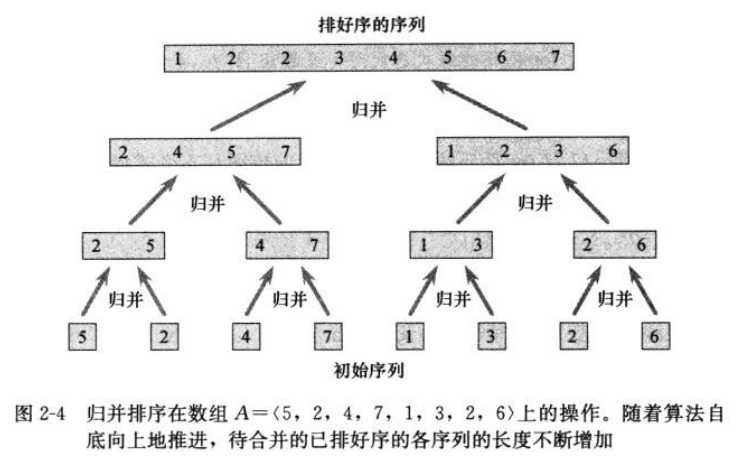
2.3.2分析分治算法
3.函数的增长
3.1渐近记号
3.2标准记号与常用函数
单调性
向下取整和向上取整
摸运算
多项式
指数
对数
阶乘
多重函数
多重对数函数
斐波那契数
4.分治策略
4.1最大子数组问题
4.2矩阵乘法的Strassen算法
4.3用代入法求解递归式
4.4用递归树方法求解递归式
4.5用主方法求解递归式
4.6证明主定理
5.概率分线和随机算法
5.1雇佣问题
5.2指示器随机变量
5.3随机算法
5.4概率分析和指示器随机变量的进一步使用
6.堆排序
6.1堆
二叉堆
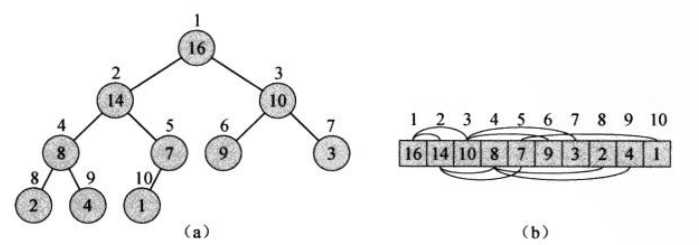
6.2维护堆的性质
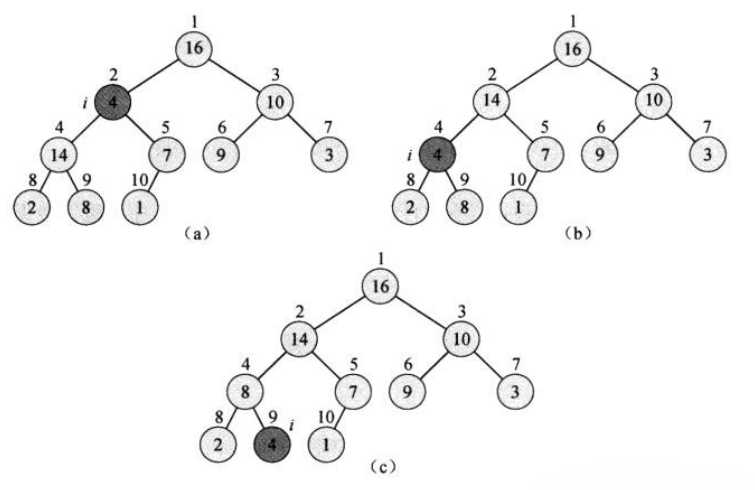
6.3建堆
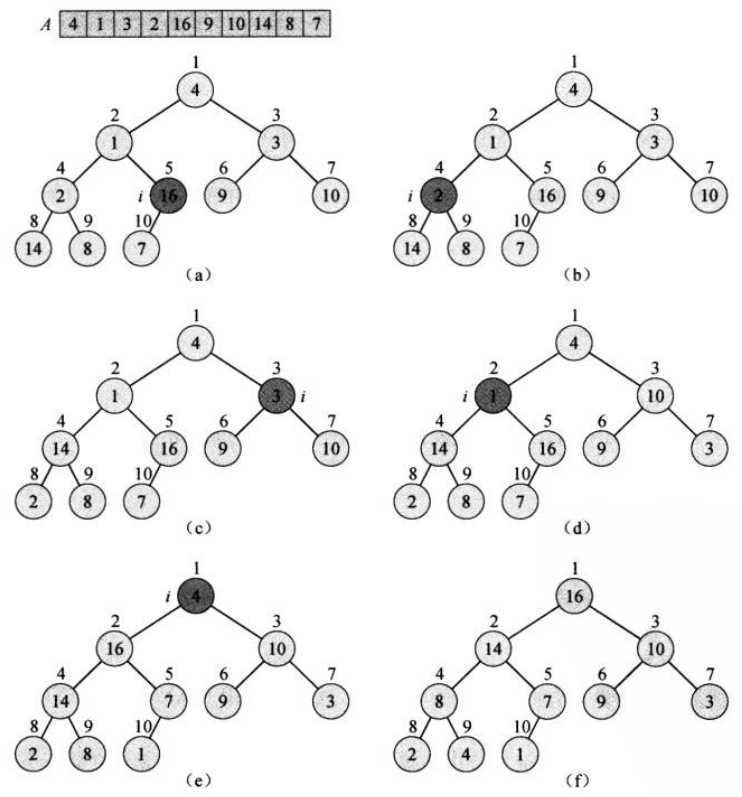
6.4堆排序算法
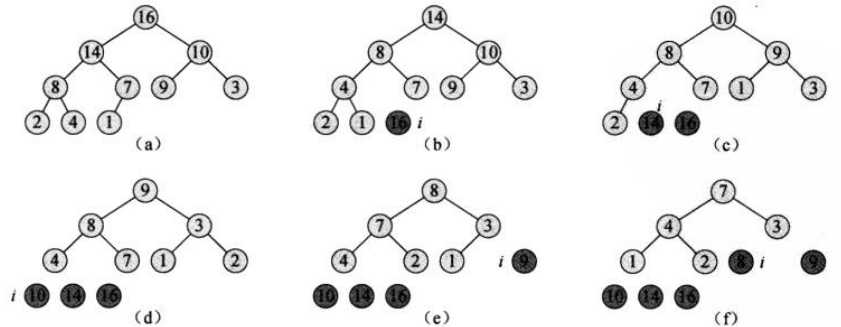
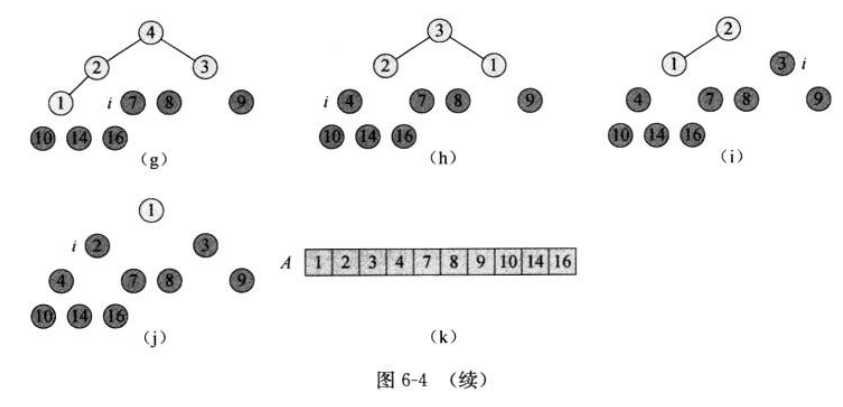
6.5优先队列
7.快速排序
7.1快速排序的描述
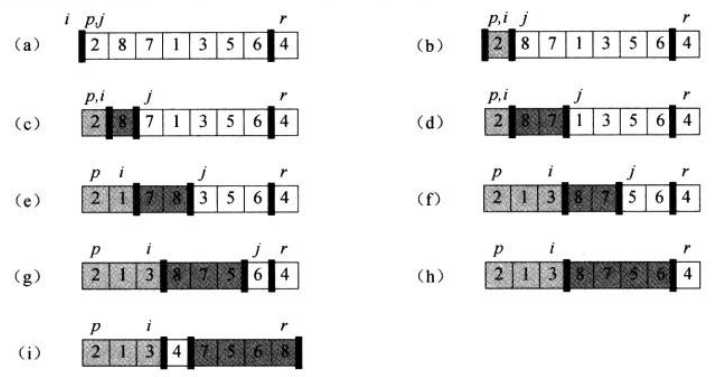
7.2快速排序的性能
7.3快速排序的随机化版本
7.4快速排序分析
8.线性时间排序
8.1排序算法的下界
8.2计数排序
8.3基数排序

8.4桶排序
9.中位数和顺序统计量
9.1最小值和最大值
9.2期望为线性时间的选择算法
9.3最坏情况为线性时间的选择算法
10.基本数据结构
10.1栈和队列
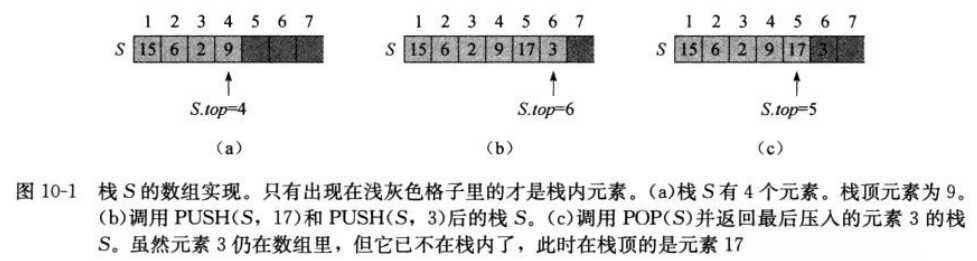
栈,后入先出
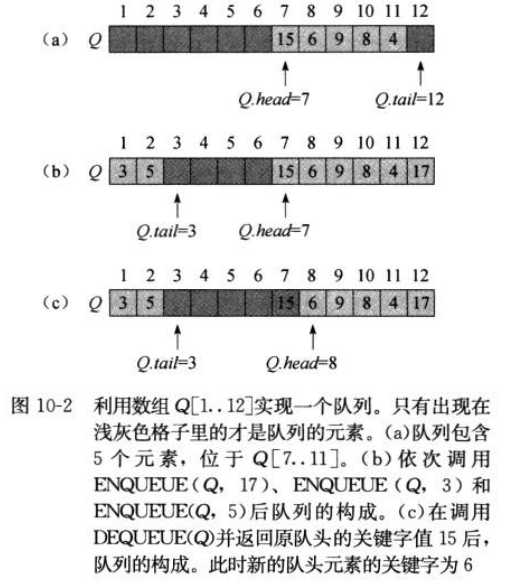
队列
10.2链表
双向链表
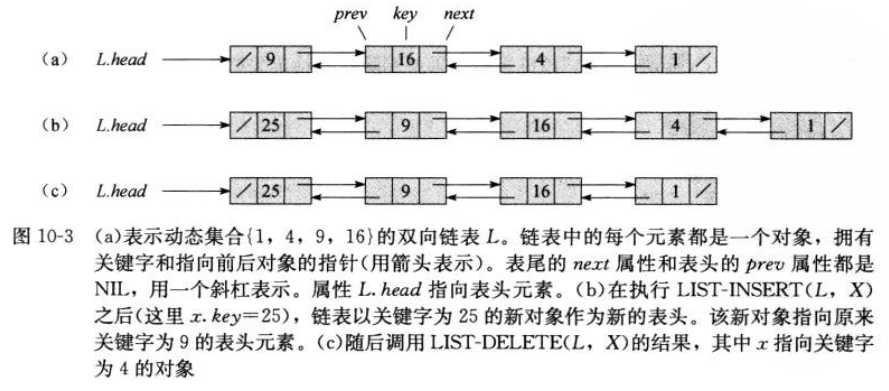
链表的搜索
链表的插入
链表的删除
哨兵,简化边界条件的处理
10.3指针和对象的实现
对象的多数组表示
对象的单数组表示
对象的分配与释放
10.4有根树的表示
二叉树
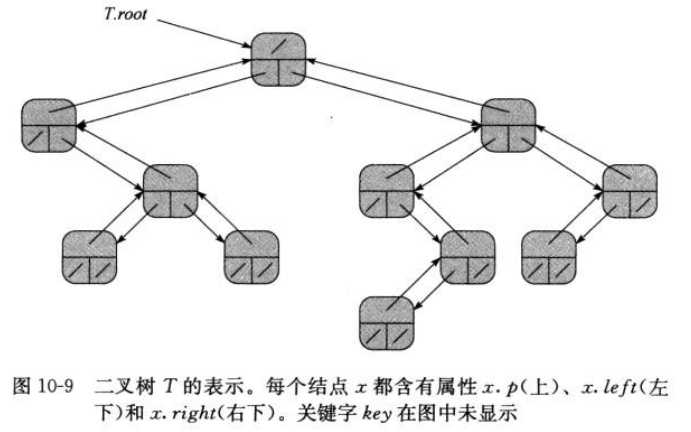
分支无限制的有根树
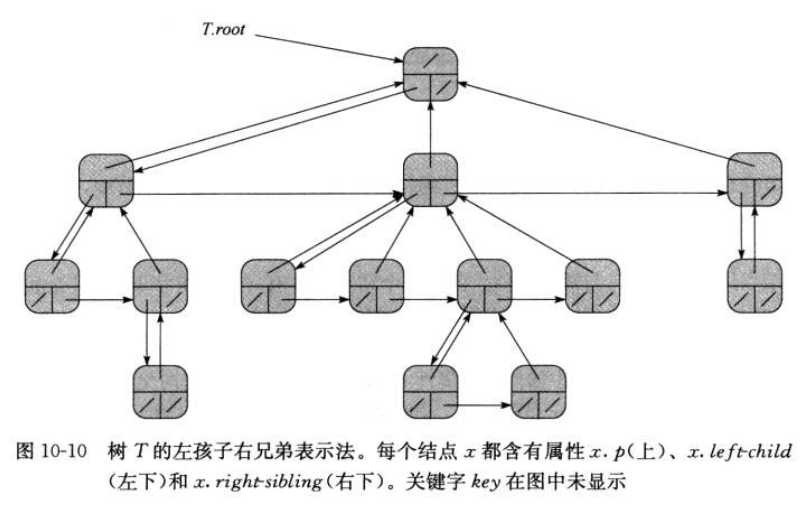
11.散列表
11.1直接寻址表
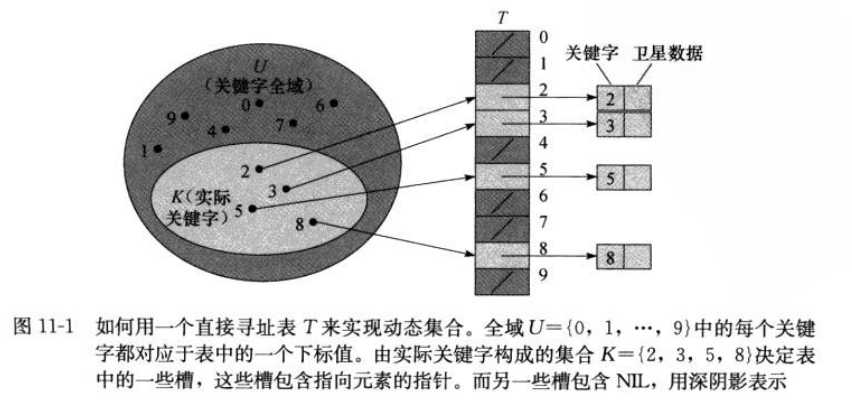
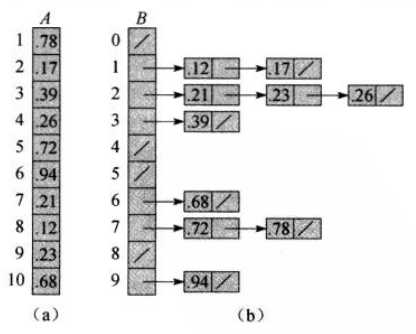
11.2散列表
通过链接法解决冲突
链接法散列的分析
11.3散列函数
11.3.1除法散列法
11.3.2乘法散列
11.3.3全域散列法
11.4开放寻址法
11.5完全散列
12.二叉搜索树
12.1什么是二叉搜索树
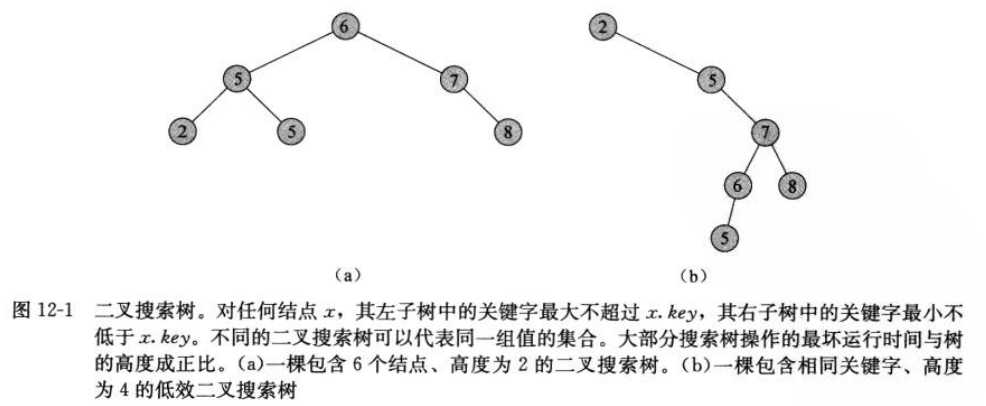
12.2查询二叉搜索树
12.3插入和删除
12.4随机构建二叉搜索树
13.红黑树
13.1红黑树的性质
13.2旋转
13.3插入
13.4删除
14.数据结构的扩张
14.1动态顺序统计
14.2如何扩张数据结构
14.3区间树
15.动态规划
15.1钢条切割
15.2矩阵链乘法
15.3动态规划原理
15.4最长公有子序列
15.5最优二叉搜索树
16.贪心算法
16.1活动选择问题
16.2贪心算法原理
16.3赫夫曼编码
16.4用拟阵求解任务调度问题
17.摊还分析
17.1聚合分析
17.2核算法
17.3势能法
17.4动态表
18.B树
18.1B树的定义
18.2B树的基本操作
18.3从B树中删除关键字
19.斐波那契堆
19.1斐波那契堆结构
19.2可合并堆操作
19.3最大度数的界
20.van Emde Boas树
20.1基本方法
20.2递归结构
20.3van Emde Boas树及其操作
21.用于不相交集合的数据结构
21.1不相交集合的操作
21.2不相交集合的链表表示
21.3不相交集合森林
21.4带路径压缩的按秩合并的分析
22.基本的图算法
22.1图的表示
22.2广度优先搜索
22.3深度优先搜索
22.4拓扑排序
22.5强连通分量
23.最小生成树
23.1最小生成树的形成
23.2Kruskal算法和Prim算法
24.单源最短路径
24.1BellmanFord算法
24.2有向无环图中的单源最短路径问题
24.3Dijkstra算法
24.4差分约束和最短路径
24.5最短路径性质的证明
25.所有节点对的最短路径问题
25.1最短路径和矩阵乘法
25.2Floyd-Warshall算法
25.3用于稀疏图的Johson算法
26.最大流
26.1流网络
26.2Ford-Fulkerson方法
26.3最大二分匹配
26.4推送-重贴标签算法
26.5前置重贴标签算法
27.多线程算法
27.1动态多线程基础
27.2多线程矩阵乘法
27.3多线程归并排序
28.矩阵运算
28.1求解性方程组
28.2矩阵求逆
28.3对称正定矩阵和最小二乘逼近
29.线性规划
29.1标准型和松弛型
29.2将问题表达为线性规划
29.3单纯性算法
29.4对偶性
29.5初始基本可行解
30.多项式与快速傅里叶变换
30.1多项式的表示
30.2DET与FFT
30.3高效FFT实现
31.数论算法
31.1基础数论概念
31.2最大公约数
31.3摸运算
31.4求解模线性方程
31.5中国余数定理
31.6元素的冥
31.7RSA公钥加密系统
31.8素数的测试
31.9整数的因子分解
32.字符串匹配
32.1朴素字符串匹配算法
32.2Rabin-Karp算法
32.3利用有限自动机进行字符串匹配
32.4Knuth-Morris-Pratt
33.计算几何学
33.1线段的性质
33.2确定任意一对线段是否相交
32.3寻找凸包
32.4寻找最近点
34.NP完全性
34.1多项式时间
34.2多项式时间的验证
34.3NP挖权限与可规约性
34..4NP完全性的证明
34.5NP完全问题
35.近似算法
35.1顶点覆盖问题
35.2旅行商问题
35.3集合覆盖问题
35.4随机化和线性规划
35.5子集和问题
标签:fft stat 矩阵链 有助于 数论 拓扑排序 傅里叶变换 无限 bellman
原文地址:https://www.cnblogs.com/plxz/p/9559394.html