标签:伪代码 == 策略 array integer 数组 com oat 哨兵
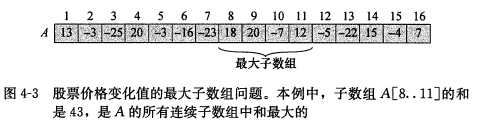
1.描述:找出数组A的和最大的非空连续子数组,我们称这样的连续子数组为最大子数组。
2. 用分治策略来求解。
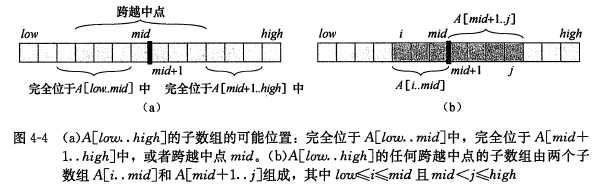
a. 假设我们要求A的子数组A[low, high]的最大子数组。根据分治策略,我们先将A[low,high] 平分
b. 那么 A[low,highj]的子数组A[i,j]只有三种可能
a)完全位于A[low, mid]; 此时 low <= i <= j <= mid
b) 完全位于A[nid+1, high]中,此时 mid + 1 <= i <= j <= high
c) 跨越了中点mid, 此时 low <= i <= mid < j < high
3. 伪代码
FIND-MAXIMUM-SUBARRAY(A, low, high) if high == low return (low, high. A[low]) //只有一个元素 else mid = (low + high)/2 //向下取整 (left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid) (right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid + 1, high) (cross-low, cross-high, cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high) if left-sum >= right-sum and left-sum >= cross-sum return (left-low, left-high, left-sum) else if right-sum >= left-sum and right-sum >= cross-sum return (right-low, right-high, right-sum) return (cross-low, cross-high, cross-sum) FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high) left-sum = -∞ sum = 0 for i = mid downto low sum = sum + A[i] if sum > left-sum left-sum = sum max-left = i right-sum = -∞ sum =0; for j = mid + 1 to high sum = sum + A[j] if sum > right-sum right-sum = sum max-right = j return (max-left, max-right, left-sum + right-sum)
4. 分析
我之前说过,所有的比较最后都是两个数比较。把最大子数组通过分治策略最后都是一个元素,这时候就是直接返回这个数,交给上一层。
这时候数组有两个数,子数组就到了2所说的比较三种情况,再一层层向上递交结果
5. 代码实现
java
public class MaxArray { private static class Result { int low; int high; int sum; public Result(int low, int high, int sum) { this.low = low; this.high = high; this.sum = sum; } } static Result findMaximumSubarray(int[] A, int low, int high) { if (low == high) { return new Result(low, high, A[low]); } else { int mid = (low + high)/2; Result leftResult = findMaximumSubarray(A, low, mid); Result rightResult = findMaximumSubarray(A, mid+1, high); Result crossResult = findMaxCrossingSubarray(A, low, mid, high); if (leftResult.sum >= rightResult.sum && leftResult.sum >= crossResult.sum) return leftResult; else if (rightResult.sum >= leftResult.sum && rightResult.sum >= crossResult.sum) return rightResult; else return crossResult; } } static Result findMaxCrossingSubarray(int[] A, int low, int mid, int high) { //向左试探 int leftSum = Integer.MIN_VALUE; //哨兵 int maxLeft = mid; int sum = 0; for (int i = mid; i >= low; i--) { sum += A[i]; if (sum > leftSum) { leftSum = sum; maxLeft = i; } } //向右试探 int rightSum = Integer.MIN_VALUE; int maxRight = mid + 1; sum = 0; for (int j = mid + 1; j <= high; j++) { sum += A[j]; if (sum > rightSum) { rightSum = sum; maxRight = j; } } //将两边的结果合起来 return new Result(maxLeft, maxRight, leftSum + rightSum); } public static void main(String[] args) { int[] A = {-1, 5, 6, 9, 10, -9, -8, 100, -200}; Result result = findMaximumSubarray(A, 0, A.length-1); System.out.println(result.low + "," + result.high + " " + result.sum); } }
python
def find_maximum_subarray(nums, low, high): if low == high: return {"low": low, "high": high, "sum": nums[low]} else: mid = int((low + high) / 2) left_result = find_maximum_subarray(nums, low, mid) right_result = find_maximum_subarray(nums, mid + 1, high) cross_result = find_max_crossing_subarray(nums, low, mid, high) if left_result["sum"] >= right_result["sum"] and left_result["sum"] >= cross_result["sum"]: return left_result else: if right_result["sum"] >= left_result["sum"] and right_result["sum"] >= cross_result["sum"]: return right_result else: return cross_result def find_max_crossing_subarray(nums, low, mid, high): left_sum = -float(‘inf‘) total = 0 max_left = mid for i in range(mid, low-1, -1): total += nums[i] if total > left_sum: left_sum = total max_left = i rigth_sum = -float(‘inf‘) total = 0 max_right = mid + 1 for j in range(mid+1, high+1): total += nums[j] if total > rigth_sum: rigth_sum = total max_right = j return {"low": max_left, "high": max_right, "sum": left_sum + rigth_sum} if __name__ == "__main__": numss = [-1, 5, 6, 9, 10, -9, -8, 100, -200] result = find_maximum_subarray(numss, 0, len(numss)-1) print(result)
再分享个python用切片的方法
def find_maximum_subarray_slice(nums): max_sum = -float(‘inf‘) result = {} for i in range(len(nums)+1): for j in range(i, len(nums)+1): total = sum(nums[i:j]) if total > max_sum: max_sum = total result["low"] = i result["high"] = j-1 result["sum"] = max_sum return result
C语言
结构体没有学好,晚点贴。。
标签:伪代码 == 策略 array integer 数组 com oat 哨兵
原文地址:https://www.cnblogs.com/yeyeck/p/9574778.html