算法之逻辑回归

标签：差值   场景   问题   事件   比较   垂直   类别   逻辑回归   变换   

logistic回归，是一种广义的线性回归分析模型，logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用。

一、逻辑回归定义

假设在多个独立自变量??1，??2，… 作用下，记y取1的概率是p=P(y=1|X)，取0的概率则为1-p

取1和取0的概率之比为p/(1-p)，称为事件的优势比（odds），对odds取自然对数即得logistic变换logit( p ) = ln( p/(1?p) )

令logit( p ) = ln( p/(1?p) ) = z,即可得p= 1/（1+e^-z ）即为logistic函数

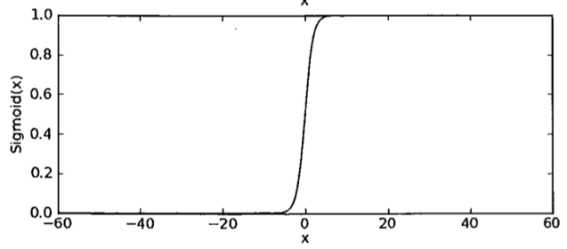
上述1/（1+e^-z ）即为sigmoid函数，其中z=β₀+β₁??1+β₂??1+β₃??1+...

之所以使用sigmoid函数，就是让样本点经过运算后得到的结果限制在0~1之间，压缩数据的巨幅震荡，从而方便得到样本点的分类标签（分类以sigmoid函数的计算结果是否大于0.5为依据）

注：因变量为分类变量，将自变量映射到（0,1）区间上

二、算法思想

Lineage回归分类算法就是将线性回归应用在分类场景中

在该场景中，计算结果是要得到对样本数据的分类标签，而不是得到那条回归直线

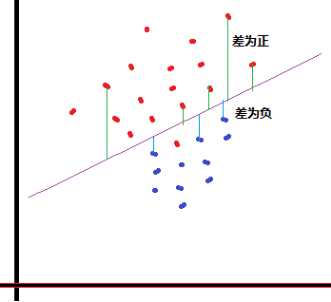
1) 算法目标

计算各点的y值到拟合线的垂直距离，如果

距离>0， 分为类A

距离<0， 分为类B

2) 如何得到拟合线

只能先假设，因为线或面的函数都可以表达成

y(拟合)=β₀+β₁??1+β₂??1+β₃??1+...

其中的β是待定参数

而??是数据的各维度特征值

因而上述问题就变成了 样本y(x) - y(拟合) >0 ? A : B

3) 如何求解出一套最优的β参数

基本思路：代入“先验数据”来逆推求解

但针对不等式求解参数极其困难

通用的解决办法，将对不等式的求解做一个转换：

1. 将“样本y(x) - y(拟合) ”的差值压缩到一个0~1的小区间，
2. 然后代入大量的样本特征值，从而得到一系列的输出结果；
3. 再将这些输出结果跟样本的先验类别比较，并根据比较情况来调整拟合线的参数值，从而是拟合线的参数逼近最优

从而将问题转化为逼近求解的典型数学问题

三、算法实现

算法思想的数学表述：

把数据集的特征值设为??1，??2，??3......

求出它们的回归系数β_i

设z=β₀+β₁??1+β₂??1+β₃??1+..... ，然后将z值代入sigmoid函数并判断结果，即可得到分类标签

问题在于如何得到一组合适的参数β_i？

通过解析的途径很难求解，而通过迭代的方法可以比较便捷地找到最优解

简单来说，就是不断用样本特征值代入算式，计算出结果后跟其实际标签进行比较，根据差值来修正参数，然后再代入新的样本值计算，循环往复，直到无需修正或已到达预设的迭代次数

注：此过程用梯度上升法来实现，获取对数似然函数的最大值

算法之逻辑回归

标签：差值   场景   问题   事件   比较   垂直   类别   逻辑回归   变换   

原文地址：https://www.cnblogs.com/dangjf/p/9579956.html