标签:输出 问题: alt 输入 ora 区间 pre 输入输出 class
如题,已知一个数列,你需要进行下面两种操作:
1.将某一个数加上x
2.求出某区间每一个数的和
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
样例说明:
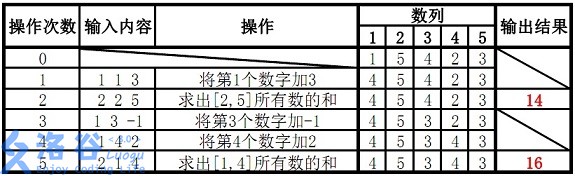
故输出结果14、16
为什么用树状数组?先问几个问题:
1. 给一串数列,几次操作,每次操作把要求的数加上某个数(也就是对这个数字修改)
我们用一个数组,O(1) 可以做到
2. 给一串数列,几次操作,每次操作把要求的区间和求出
这也简单,利用前缀和做完预处理,O(1) 也可以做到
但,既要修改,又要求前缀和呢?
还按上述做法,我们每修改一次,前缀和就要重新更新,多次操作下来,将非常耗时间
于是,一个神奇的做法出现——树状数组
它好在一个 lowbit 操作,再修改单点的同时,以一种神奇的方法,快速地更新了区间和
具体讲解参考教材
代码
#include<stdio.h> const int Mx=500001; int a[Mx],c[Mx]; int n,m; int lowbit(int x) { return x&-x; } void add(int x,int tx) { for(int i=x;i<=n;i+=lowbit(i)){ c[i]+=tx; } } int ask(int x) { int tot=0; for(int i=x;i;i-=lowbit(i)) tot+=c[i]; return tot; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;++i){ scanf("%d",&a[i]); add(i,a[i]); } while(m--){ int kiss; scanf("%d",&kiss); if(kiss==1){ int kis,jia; scanf("%d%d",&kis,&jia); add(kis,jia); } else if(kiss==2){ int l,r; scanf("%d%d",&l,&r); printf("%d\n",ask(r)-ask(l-1)); } } return 0; }
标签:输出 问题: alt 输入 ora 区间 pre 输入输出 class
原文地址:https://www.cnblogs.com/qseer/p/9581830.html