标签:分支 遍历 dstat 分享 元素 所有结点 b2b 表示 binary
树(英语:tree)是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
特点:每个节点有另个或者多个节点;没有父节点的节点分为根节点;每个非根节点只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树;
相关术语
树种类:
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
二叉树:每个节点最多含有两个子树的树称为二叉树;
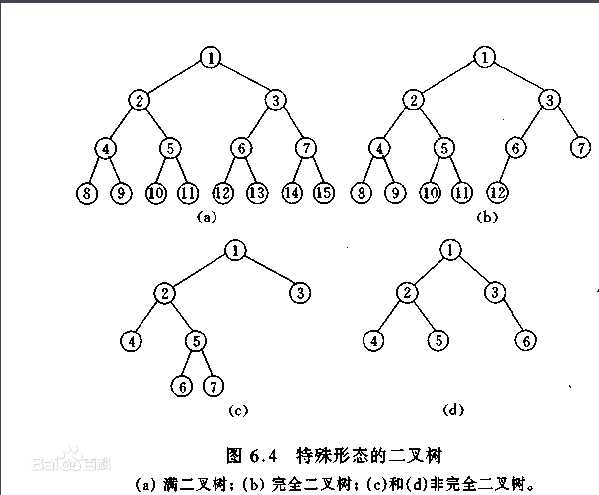
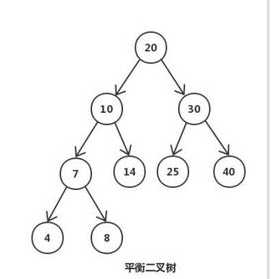
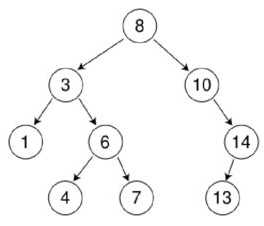
霍夫曼树(用于信息编码):带权路径最短的二叉树称为哈夫曼树或最优二叉树;给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
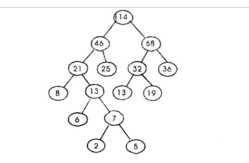
B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树。
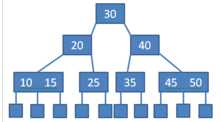
二叉树定义:二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树性质
二叉树的遍历,
先序遍历:遍历顺序规则为【根左右】
中序遍历:遍历顺序规则为【左根右】
后序遍历:遍历顺序规则为【左右根】
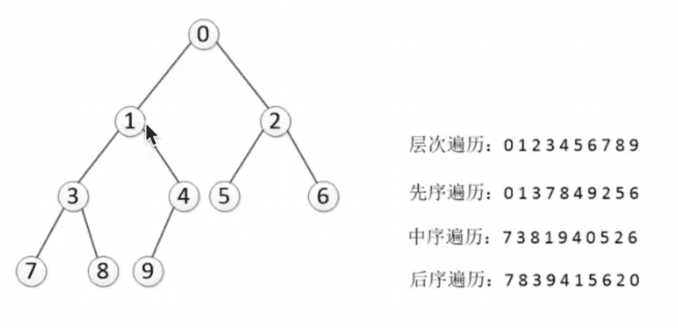
代码实现

# Author:song class Node(object): def __init__(self,item): self.elem = item self.lchild = None self.rchild = None class Tree(object): """二叉树""" def __init__(self): self.root = None def add(self,item): node = Node(item) if self.root is None: self.root = node return queue = [self.root] while queue: cur_node = queue.pop(0) if cur_node.lchild is None: cur_node.lchild = node return else: queue.append(cur_node.lchild) if cur_node.rchild is None: cur_node.rchild = node return else: queue.append(cur_node.rchild) def breadth_travel(self): """广度遍历""" if self.root is None: return queue = [self.root] while queue: cur_node = queue.pop(0) print(cur_node.elem,end=‘,‘) if cur_node.lchild is not None: queue.append(cur_node.lchild) if cur_node.rchild is not None: queue.append(cur_node.rchild) print(‘‘) def preorder(self,node): """先序遍历""" if node is None: return print(node.elem,end=‘,‘) self.preorder(node.lchild) self.preorder(node.rchild) def inorder(self,node): """中序遍历""" if node is None: return self.inorder(node.lchild) print(node.elem, end=‘,‘) self.inorder(node.rchild) def posorder(self,node): """后序遍历""" if node is None: return self.posorder(node.lchild) self.posorder(node.rchild) print(node.elem, end=‘,‘) if __name__ == "__main__": tree = Tree() tree.add(0) tree.add(1) tree.add(2) tree.add(3) tree.add(4) tree.add(5) tree.add(6) tree.add(7) tree.add(8) tree.add(9) print(‘广度优先:‘) tree.breadth_travel() print(‘先序遍历:‘) tree.preorder(tree.root) print(‘‘) print(‘中序遍历:‘) tree.inorder(tree.root) print(‘‘) print(‘后序遍历:‘) tree.posorder(tree.root) 结果: 广度优先: 0,1,2,3,4,5,6,7,8,9, 先序遍历: 0,1,3,7,8,4,9,2,5,6, 中序遍历: 7,3,8,1,9,4,0,5,2,6, 后序遍历: 7,8,3,9,4,1,5,6,2,0,
通过两个序列可以确定一棵树,其中必定有中序,只给先序后序无法确定一棵树。
标签:分支 遍历 dstat 分享 元素 所有结点 b2b 表示 binary
原文地址:https://www.cnblogs.com/master-song/p/9608490.html