标签:ini john img 上下 解决 people pac xpl arm
所谓01分数规划,看到这个名字,可能会想到01背包,其实长得差不多。
这个算法就是要求“性价比”最高的解。sum(v)/sum(w)最高的解。
我们给定两个数组,a[i]表示选取i的收益,b[i]表示选取i的代价。如果选取i,定义x[i]=1否则x[i]=0。每个物品只有选和不选的两种方案,求一个选择的方案使得R=sigma(a[i]x[i])/sigma(b[i]x[i]),也就是选择物品的总收益/总代价最大或者最小。
01分数规划问题主要包含以下几个问题:
F(L)=sigma(a[i]x[i])-Lsigma(b[i]x[i])
F(L)=sigma(a[i]x[i]-Lb[i]a[i])
F(L)=sigma((a[i]-Lb[i])x[i])
我们把a[i]-L*b[i]定义为d[i],这样我们的算式就变成了以下算式。
F(L)=sigma(d[i]*x[i])
这样我们就把这个繁琐的算式变成了一个非常优美的算式。
而01分数规划就是要枚举L在求最大值或最小值的F(L)。
在实现程序的过程中,我们使用一个非常熟悉的老朋友,要求最大或最小,所以??我们就要用二分
(个人看法)
如果硬要贪心,那么就只有可能是算出每一个物品的性价比,在排序求出最大或者最小的性价比,在累加算出答案。
先设置价值数组a[i]和代价数组b[i],我们的答案为R。
\[ R= \frac{\sum_{i=1}^{n}{a[i]*x[i]}}{\sum_{i=1}^{n}{b[i]*x[i]}}\]
简单来说 \[ R=\frac{\sum{valuei}}{\sum{weighti}} \]
我们可以发现,R的大小与上下的总值有关。
我们反观一下贪心算法,先算出每个物品的性价比
\[ xi=\frac {valuei}{weighti}\]
那么贪心得到的答案就是
\[ R=\sum{xi}\]
我们可以很容易发现,01分数规划和贪心的得到的答案有明显的区别,一个是总价值/总代价,而贪心中只是单价值/单代价的累加,而不只是比值的大小,而取决于分母和分子的大小,所以这两个东西不相等
In a certain course, you take n tests. If you get ai out of bi questions correct on test i, your cumulative average is defined to be
\[ 100*\frac{\sum_{i=1}^{n}{ai}}{\sum_{i=1}^{n}{ai}}\]
Given your test scores and a positive integer k, determine how high you can make your cumulative average if you are allowed to drop any k of your test scores.
Suppose you take 3 tests with scores of 5/5, 0/1, and 2/6. Without dropping any tests, your cumulative average is . However, if you drop the third test, your cumulative average becomes .
Input
3 1
5 0 2
5 1 6
4 2
1 2 7 9
5 6 7 9
0 0
Sample Output
83
100
Analysis
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cctype>
#include <cmath>
#include <time.h>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define ms(a,b) memset(a,b,sizeof(a))
typedef long long ll;
const double eps=1e-7;
int n,k;
double a[1010],b[1010],d[1010];
inline int read()
{
int X=0,w=0; char ch=0;
while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
int main()
{
while (1)
{
n=read(),k=read();
if (n==0 && k==0) break;
for (int i=1;i<=n;i++) scanf("%lf",&a[i]);
for (int i=1;i<=n;i++) scanf("%lf",&b[i]);
double l=0.0,r=1.0,mid;
while (r-l>eps)
{
mid=(l+r)/2;
for (int i=1;i<=n;i++) d[i]=a[i]-mid*b[i];
sort(d+1,d+1+n);
double sum=0.0;
for (int i=k+1;i<=n;i++) sum+=d[i];
if (sum>0) l=mid;
else r=mid;
}
printf("%.0f\n",mid*100);
}
return 0;
}N个物品的体积为W1,W2......Wn(Wi为整数),与之相对应的价值为P1,P2......Pn(Pi为整数),从中选出K件物品(K <= N),使得单位体积的价值最大。
Input
3 2
2 2
5 3
2 1
Sample Output
3/4
Analysis
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cctype>
#include <cmath>
#include <time.h>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define ms(a,b) memset(a,b,sizeof(a))
typedef long long ll;
const int maxn = 50005;
const double eps = 1e-9;
ll gcd(ll x,ll y){return y?gcd(y,x%y):x;}
struct node
{
int w,p;
double val;
bool operator < (const node& T) const{
return val>T.val;
}
}b[maxn];
double mid;
ll anss,ansx,tmps,tmpx;
int n,k;
bool check()
{
int tot=0;
for(int i=0;i<n;i++)b[i].val = 1.0*b[i].p-b[i].w*mid;
sort(b,b+n);
double sum=0;
tmps=0,tmpx=0;
for(int i=0;i<k;i++)sum+=b[i].val,tmps+=b[i].p,tmpx+=b[i].w;
if(sum-0>=eps)return true;
return false;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++) scanf("%d%d",&b[i].w,&b[i].p);
double l=0,r=500000;
for(int i=0;i<100;i++)
{
mid=(l+r)/2;
if(check())l=mid,anss=tmps,ansx=tmpx;
else r=mid;
}
ll tmp=gcd(anss,ansx);
anss/=tmp,ansx/=tmp;
printf("%lld/%lld\n",anss,ansx);
return 0;
}David the Great has just become the king of a desert country. To win the respect of his people, he decided to build channels all over his country to bring water to every village. Villages which are connected to his capital village will be watered. As the dominate ruler and the symbol of wisdom in the country, he needs to build the channels in a most elegant way.
After days of study, he finally figured his plan out. He wanted the average cost of each mile of the channels to be minimized. In other words, the ratio of the overall cost of the channels to the total length must be minimized. He just needs to build the necessary channels to bring water to all the villages, which means there will be only one way to connect each village to the capital.
His engineers surveyed the country and recorded the position and altitude of each village. All the channels must go straight between two villages and be built horizontally. Since every two villages are at different altitudes, they concluded that each channel between two villages needed a vertical water lifter, which can lift water up or let water flow down. The length of the channel is the horizontal distance between the two villages. The cost of the channel is the height of the lifter. You should notice that each village is at a different altitude, and different channels can‘t share a lifter. Channels can intersect safely and no three villages are on the same line.
As King David‘s prime scientist and programmer, you are asked to find out the best solution to build the channels.
Input
4
0 0 0
0 1 1
1 1 2
1 0 3
0
Sample Output
1.000
Analysis
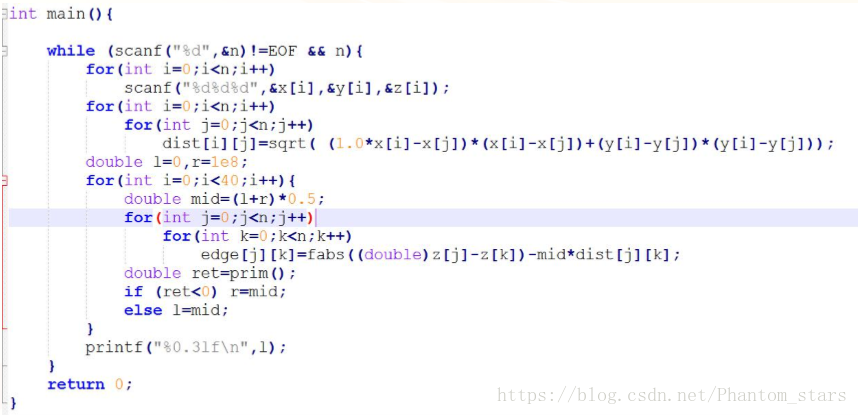
Farmer John has decided to reward his cows for their hard work by taking them on a tour of the big city! The cows must decide how best to spend their free time.
Fortunately, they have a detailed city map showing the L (2 ≤ L ≤ 1000) major landmarks (conveniently numbered 1.. L) and the P (2 ≤ P ≤ 5000) unidirectional cow paths that join them. Farmer John will drive the cows to a starting landmark of their choice, from which they will walk along the cow paths to a series of other landmarks, ending back at their starting landmark where Farmer John will pick them up and take them back to the farm. Because space in the city is at a premium, the cow paths are very narrow and so travel along each cow path is only allowed in one fixed direction.
While the cows may spend as much time as they like in the city, they do tend to get bored easily. Visiting each new landmark is fun, but walking between them takes time. The cows know the exact fun values Fi (1 ≤ Fi ≤ 1000) for each landmark i.
The cows also know about the cowpaths. Cowpath i connects landmark L1i to L2i (in the direction L1i -> L2i ) and requires time Ti (1 ≤ Ti ≤ 1000) to traverse.
In order to have the best possible day off, the cows want to maximize the average fun value per unit time of their trip. Of course, the landmarks are only fun the first time they are visited; the cows may pass through the landmark more than once, but they do not perceive its fun value again. Furthermore, Farmer John is making the cows visit at least two landmarks, so that they get some exercise during their day off.
Help the cows find the maximum fun value per unit time that they can achieve.
Input
5 7
30
10
10
5
10
1 2 3
2 3 2
3 4 5
3 5 2
4 5 5
5 1 3
5 2 2
Sample Output
6.00
Analysis
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#define N 100010
using namespace std;
const double eps=1e-5;
struct edge
{
int v,nxt,w;
double c;
} e[N<<1];
int head[N],f[N];
bool vis[N];
double dis[N];
int n,m,mct,u,v,w;
inline int read()
{
int x=0,f=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
void add(int u,int v,int w)
{
e[++mct].v=v;e[mct].nxt=head[u];e[mct].w=w;head[u]=mct;
}
bool spfa(int u)
{
vis[u]=1;
for(int i=head[u]; i; i=e[i].nxt)
{
int v=e[i].v;
if(dis[v]>dis[u]+e[i].c)
{
dis[v]=dis[u]+e[i].c;
if(vis[v] || spfa(v))
{
vis[v]=0;
return 1;
}
}
}vis[u]=0;return 0;
}
void judge(double r)
{
for(int i=1; i<=mct; i++)
e[i].c=(double)e[i].w*r-f[e[i].v];
return;
}
bool check()
{
for(int i=1; i<=n; i++)
if(spfa(i))return 1;
return 0;
}
int main()
{
n=read();m=read();
for(int i=1; i<=n; i++) f[i]=read();
for(int i=1; i<=m; i++)
{
u=read();v=read();w=read();
add(u,v,w);
}
double l=0,r=100000,ans;
while(r-l>eps)
{
double mid=(l+r)/2;
judge(mid);
if(check())
{
ans=mid;l=mid;
}
else r=mid;
}
printf("%.2f\n",ans);
return 0;
}标签:ini john img 上下 解决 people pac xpl arm
原文地址:https://www.cnblogs.com/Dawn-Star/p/9610410.html