算法学习(一)

标签：bsp   ios   .cpp   交换变量   过程   include   结束   模块化   实现   

主要内容：

• 通过一道例题介绍算法设计的过程，及在设计与分析问题中运用的技巧及思想（c/c++实现）。

例题：求两个正整数的最大公约数。

1. 数学模型：a，b > 0 的整数，求能c，c能整除a，b且a/c与b/c互质（没有公约数）。
2. 问题分析：
   • 分解因数法：a与b能共同整除的最大因数。
   • 分解质因数法：a与b能共同整除的质因数相乘
   • 短除法：所有公约数相乘。
   • 辗转相除法：?
3. 算法描述：

分解因数法:

1. 分解因数法： ?source code

   int a, b, flag;
   input(a,b)
   if(a>b)
       a，b交换数值
   for(从a循环递减，搜索最大的公因数)
       if(能同时整除a，b即为公因数)
                 跳出循环；
   print(flag);

2. 算法说明：
   • 定义flag用于标记公因数(也可直接用 a循环，这里便于理解定义flag变量)
   • 比较a与b的大小，保证a为其中最小的数，方便下面进行循环(s-code中提供一种两变量交换数值的方法)
   • 由于要求的是最大公因数，则采取倒序搜索减少搜索次数(即从大到小)
   • 若要要求无限次键入a，b的值（即多组数据）且a或b等于0时结束输入，采用while(cin >> a >> b && a && b)输入模式：当while的条件语句中的任意条件为假停止循环(0为假，非0为真)
3. 算法分析：最好是循环1次，最坏循环a次,则T(n)=1/n(1+.....+n)=(1/n)*n*(n+1)/2=1/2*n+1/2即时间复杂度为O(n).

 分解质因数法:

1. 分解质因数法:

   #include<iostream>
   #include<cmath> 
   using namespace std;
   bool pNumber(int n)            //判断质数
   {
       for(int i = 2; i <= sqrt(n); i++)
           if(n%i == 0)
               return false;
       return true;
   }
   void exchange(int &x, int &y)    //交换x，y的值
   {
       int temp = x;
       x = y;
       y = temp;
   }
   int main()
   {
       int a, b;    
       while(cin >> a >> b && a != 0 && b != 0){
           int flag = 1;
           if(a > b)
               exchange(a, b);
           for(int i = 2; i <= a; i++)
               if(a%i == 0 && b%i == 0 && pNumber(i)){
                   flag *= i;
       //        cout << "this is debug!----" <<i << endl;    
               }
           cout << flag << endl;
       }
       return 0;
   }

2. 算法说明：
   • 采用模块化思想把main函数中的部分通用性的功能进行模块化处理（判断质数、交换变量值），自顶向下，逐步细分。
   • 借助短路与（&&）的优点，减少循环的次数:pNumber()函数放在不同位置导致的循环次数不同if(a%i == 0 && b%i == 0 && pNumber(i))  <   if(pNumber(i) &&a%i == 0 && b%i == 0 )
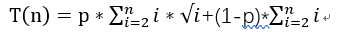3. 算法分析：假设i能同时整除a，b的概率为p，则:O(n) = n^(5/2).

短除法:

1. 短除法： 

   #include<iostream>
   #include<cmath> 
   using namespace std;
   int main()
   {
           int a, b, t, i;
           cin >> a >> b;
           t = 1;
           for(i = 2; i <= a && i <= b; i++)
               while(a%i == 0 && b%i == 0)
               {
                   t = t*i;
                   a = a/i;
                   b = b/i;
               }
           cout << t << endl;
           return 0;
   }

    

辗转相除法：

1. 1. 辗转相除法： 

      #include<iostream>
      #include<cmath> 
      using namespace std;
      int main()
      {
              int a, b, c;
              cin >> a >> b;
              if(b == 0 || a == 0)
              {
                  cout << "data error!" << endl;
                  return 0;
              }
              else
              {
                  c = a % b;
                  while(c != 0)
                  {
                      a = b;
                      b = c;
                      c = a %b;
                  }
              }
              cout << b;
              return 0;
      }

       

 ?source code------仅供参考

算法学习(一)

标签：bsp   ios   .cpp   交换变量   过程   include   结束   模块化   实现   

原文地址：https://www.cnblogs.com/sunrisepeak/p/9652968.html