标签:plane wing his problem div etc 图片 python represent
On a N * N grid, we place some 1 * 1 * 1 cubes that are axis-aligned with the x, y, and z axes.
Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).
Now we view the projection of these cubes onto the xy, yz, and zx planes.
A projection is like a shadow, that maps our 3 dimensional figure to a 2 dimensional plane.
Here, we are viewing the "shadow" when looking at the cubes from the top, the front, and the side.
Return the total area of all three projections.
Example 1:
Input: [[2]]
Output: 5
Example 2:
Input: [[1,2],[3,4]]
Output: 17
Explanation:
Here are the three projections ("shadows") of the shape made with each axis-aligned plane.
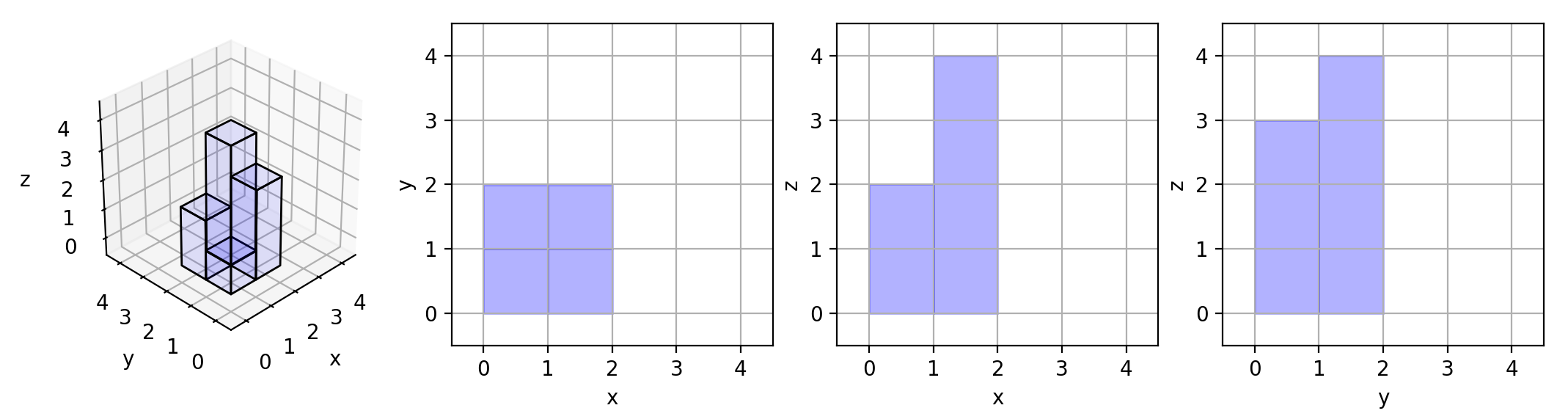
Example 3:
Input: [[1,0],[0,2]]
Output: 8
Example 4:
Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 14
Example 5:
Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 21
Note:
1 <= grid.length = grid[0].length <= 500 <= grid[i][j] <= 50
This problem is just like the problem 807. We just need to find the max element in each row and column and find the number of nonzero elements. Then the sum of them is the answer.
class Solution:
def projectionArea(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
rAf=sum([max(r) for r in grid])+sum([max(c) for c in zip(*grid)])
m=len(grid)
n=len(grid[0])
num=0
for r in grid:
num+=r.count(0)
return (m*n-num)+rAf
[LeetCode&Python] Problem 883. Projection Area of 3D Shapes
标签:plane wing his problem div etc 图片 python represent
原文地址:https://www.cnblogs.com/chiyeung/p/9695249.html