标签:提取 表达 uniq 基于 多少 class p12 net 等等
参考Kernels里面评论较高的一篇文章,整理作者解决整个问题的过程,梳理该篇是用以了解到整个完整的建模过程,如何思考问题,处理问题,过程中又为何下那样或者这样的结论等!
最后得分并不是特别高,只是到34%,更多是整理一个解决问题的思路,另外前面三个大步骤根据思维导图看即可,代码跟文字等从第四个步骤开始写起。
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(4) 会用到的库:
以下是在接下来的实验里会用到的一些库:
# data analysis and wrangling import pandas as pd import numpy as np import random as rnd # visualization import seaborn as sns import matplotlib.pyplot as plt # machine learning from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC, LinearSVC from sklearn.ensemble import RandomForestClassifier from sklearn.neighbors import KNeighborsClassifier from sklearn.naive_bayes import GaussianNB from sklearn.linear_model import Perceptron from sklearn.linear_model import SGDClassifier from sklearn.tree import DecisionTreeClassifier
(5)获取数据:
我们可以用python 的 Pandas 来帮助我们处理数据。首先可以将训练数据以及测试数据读入到Pandas 的 DataFrames 里。我们也会将这两个数据集结合起来,用于在两个数据集上同时做一些特定的操作。
# set pandas pd.set_option(‘display.width‘, 1000) # use pandas to manage data train_df = pd.read_csv(‘data/train.csv‘) test_df = pd.read_csv(‘data/test.csv‘) combine = [train_df, test_df]
(6) 通过描述数据来分析:
Pandas 也可以帮助我们描述数据集。我们可以通过以下问答的方式来查看数据集:
1. 在数据集中有哪些可用的特征?
首先需要注意的是,数据集里特征的描述已经在问题描述里给出了,此次数据集里的特征描述如下:
https://www.kaggle.com/c/titanic/data
------------------------------------------------------------------------------------------------------
主要内容为:
Data Dictionary
|
Variable |
Definition |
Key |
|
survival |
Survival |
0 = No, 1 = Yes |
|
pclass |
Ticket class |
1 = 1st, 2 = 2nd, 3 = 3rd |
|
sex |
Sex |
|
|
Age |
Age in years |
|
|
sibsp |
# of siblings / spouses aboard the Titanic |
|
|
parch |
# of parents / children aboard the Titanic |
|
|
ticket |
Ticket number |
|
|
fare |
Passenger fare |
|
|
cabin |
Cabin number |
|
|
embarked |
Port of Embarkation |
C = Cherbourg, Q = Queenstown, S = Southampton |
Variable Notes
pclass: A proxy for socio-economic status (SES)
1st = Upper
2nd = Middle
3rd = Lower
age: Age is fractional if less than 1. If the age is estimated, is it in the form of xx.5
sibsp: The dataset defines family relations in this way...
Sibling = brother, sister, stepbrother, stepsister
Spouse = husband, wife (mistresses and fiancés were ignored)
parch: The dataset defines family relations in this way...
Parent = mother, father
Child = daughter, son, stepdaughter, stepson
Some children travelled only with a nanny, therefore parch=0 for them.
------------------------------------------------------------------------------------------------------
查看训练集里面各字段:
print(train_df.columns.values)
[‘PassengerId‘ ‘Survived‘ ‘Pclass‘ ‘Name‘ ‘Sex‘ ‘Age‘ ‘SibSp‘ ‘Parch‘ ‘Ticket‘ ‘Fare‘ ‘Cabin‘ ‘Embarked‘]
PassengerId => 乘客ID
Pclass => 乘客等级(1/2/3等舱位)
Name => 乘客姓名
Sex => 性别
Age => 年龄
SibSp => 堂兄弟/妹个数
Parch => 父母与小孩个数
Ticket => 船票信息
Fare => 票价
Cabin => 客舱
Embarked => 登船港口
2. 哪些特征是离散型的?
这些离散型的数值可以将样本分类为一系列相似的样本。在离散型特征里,它们的数值是基于名词的?还是基于有序的?又或是基于比率的?还是基于间隔类的?除此之外,这个可以帮助我们为数据选择合适的图形做可视化。
在这个问题中,离散型的变量有:Survived,Sex 和 Embarked。基于序列的有:Pclass
3. 哪些特征是数值型?
哪些特征是数值型的?这些数据的值随着样本的不同而不同。在数值型特征里,它们的值是离散的还是连续的?又或者是基于时间序列?除此之外,这个可以帮助我们为数据选择合适的图形做可视化。
在这个问题中,连续型的数值特征有:Age,Fare。离散型数值有:SibSp,Parch
train_df.head()

4. 哪些特征是混合型数据?
数值型、字母数值型数据在同一特征下面。这些有可能是我们需要修正的目标数据。
在这个问题中,Ticket是混合了数值型以及字母数值型的数据类型,Cabin是字母数值型数据
5. 哪些特征可能包含错误数据或打字错误?
在大型数据集里要发现这些可能比较困难,然而通过观察小型的数据集里少量的样本,可能也可以完全告诉我们哪些特征需要修正。
在这个问题中,Name的特征可能包含错误或者打字错误,因为会有好几种方法来描述名字
#默认倒数5行 train_df.tail()
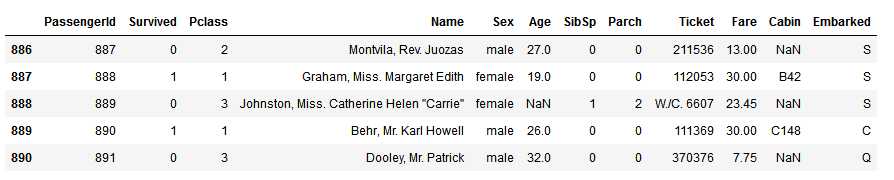
6. 哪些特征包含空格,null或者空值
这些空格,null值或者空值很可能需要修正。
在这个问题中:
7.每个特征下的数据类型是什么?
这个可以在我们做数据转换时起到较大的帮助。
在这个问题中:
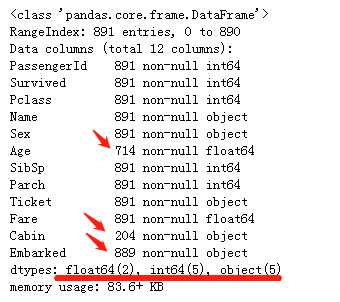
train_df.info()
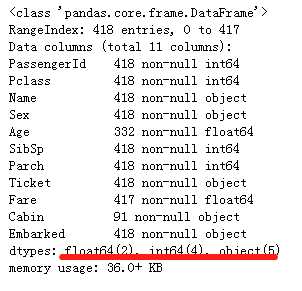
test_df.info()
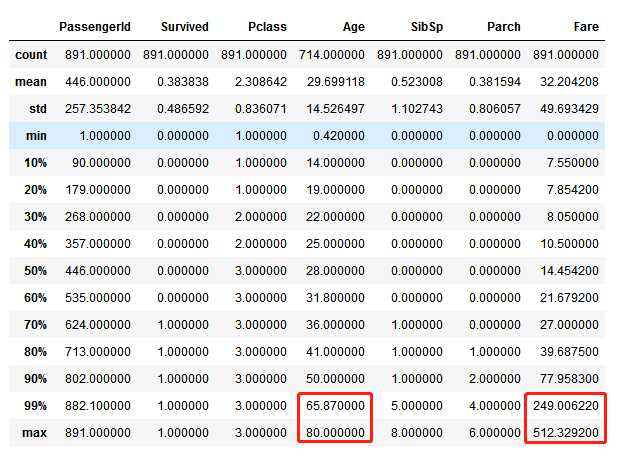
8. 在样本里,数值型特征的数值分布是什么样的?
这个可以帮助我们初步了解:训练数据集如何体现了实际问题。
在这个问题中:
我们可以通过以下方式获取上述信息:
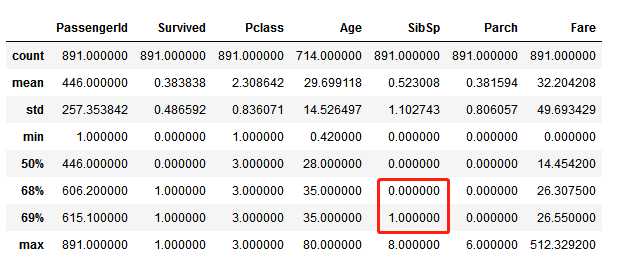
train_df.describe()
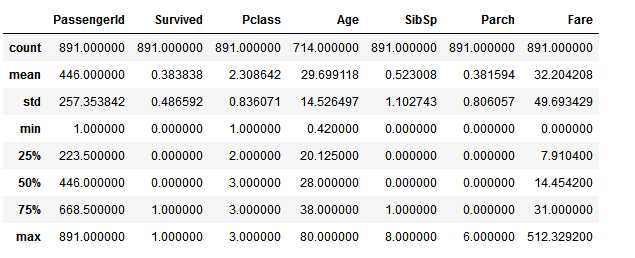
# 通过使用 percentiles=[.61, .62] 来查看数据集可以了解到生存率为 38%
train_df.describe(percentiles=[.61, .62])
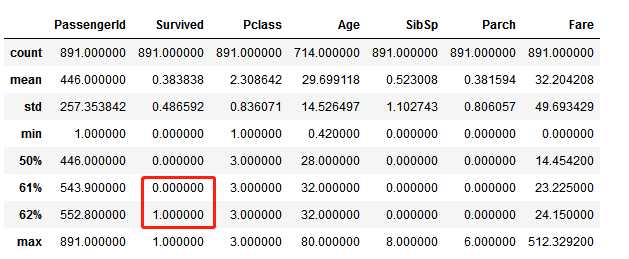
# 通过使用 percentiles=[.76, .77] 来查看Parch的分布 train_df.describe(percentiles=[.76, .77])
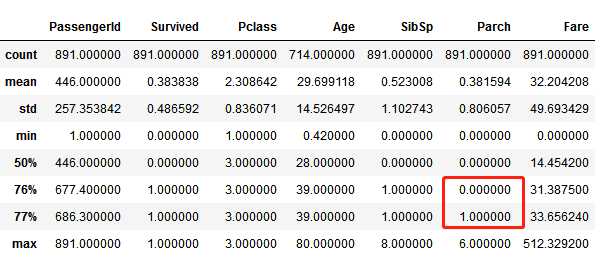
# 通过使用 percentile=[.68, .69] 来查看SibSp的分布 train_df.describe(percentiles=[.68, .69])
#通过使用 percentile=[.1, .2, .3, .4, .5, .6, .7, .8, .9, .99] 来查看Age和Fare的分布 train_df.describe(percentiles=[.1, .2, .3, .4, .5, .6, .7, .8, .9, .99])
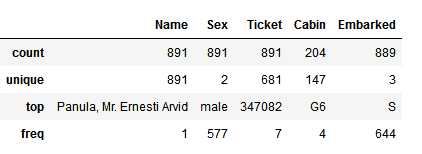
8. 在样本里,离散型数据的分布是什么?
在这个问题中:
可以通过以下方法获得以上信息:
train_df.describe(include=[‘O‘])
(7)基于以上数据分析后的假设
根据以上的数据分析步骤后,我们可以暂时得出以下假设。当然,我们也可以在之后验证这些假设。
相互关系:
我们想知道每个特征与Survival的相关性如何。我们希望能够今早的做这一步,并且将这些相关性特征匹配到建模后的相关性特征上。
补全数据:
修正数据:
创造数据:
分类:
根据之前的问题描述或者已有的数据,我们也可以提出以下假设:
(8)通过转换部分特征后的分析
为了验证之前的观察与假设,我们可以通过pivoting feature的方法简单的分析一下特征之间的相关性。
这种方法仅仅对那些没有特别多空值的属性有效,并且仅仅对那些分类型的(Sex)、有序型的(Pclass)以及离散型(SibSp,Parch)的特征才有意义。
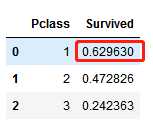
1. Pclass:我们观察到Pclass=1与Survived的相关性较大(>0.5),所以可以考虑将此特征放入到之后的模型里
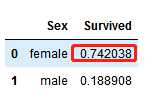
2. Sex:我们可以确认Sex=female有着高达74%的生存率
3. SibSp 和 Parch:这些特征下有些值与survived有相关性,但是有些又毫无相关性。所以我们可能需要基于这些单独的特征或一系列特征创建一个新特征,以做进一步分析
以上结论可以通过下面的操作获取:
train_df[[‘Pclass‘, ‘Survived‘]].groupby([‘Pclass‘], as_index=False).mean().sort_values(by=‘Survived‘, ascending=False)
train_df[[‘Sex‘, ‘Survived‘]].groupby([‘Sex‘], as_index=False).mean().sort_values(by=‘Survived‘, ascending=False)
train_df[[‘SibSp‘, ‘Survived‘]].groupby([‘SibSp‘], as_index=False).mean().sort_values(by=‘Survived‘, ascending=False)
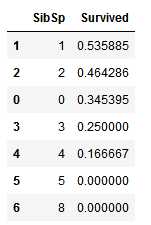
train_df[[‘Parch‘, ‘Survived‘]].groupby([‘Parch‘], as_index=False).mean().sort_values(by=‘Survived‘, ascending=False)
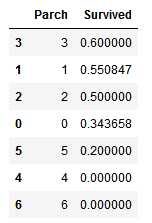
(9)通过将数据可视化进行分析
现在我们可以通过将数据可视化对数据做进一步分析,并继续验证我们之前的假设是否正确
数值型特征与Survived之间的联系:
柱状图在用于分析连续型的数值特征时非常有用,如特征Age,它的柱状图数值范围(不同的年龄范围)可以帮助我们识别一些有用的模式。
通过使用默认或自定的数值范围(年龄范围),柱状图可以帮助我们描绘出样本所遵循的分布。
它可以帮助我们发现是否某些特定的年龄范围(如婴儿)有更高的存活率。
我们可以通过以下代码来画出Age的柱状图:
g = sns.FacetGrid(train_df, col=‘Survived‘) g.map(plt.hist, ‘Age‘, bins=20) plt.show()
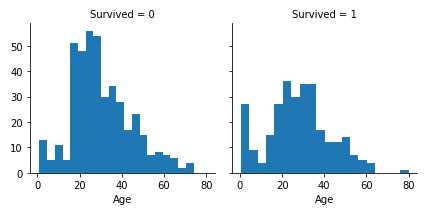
观察:
结论:
以上简单的分析验证了我们之前的假设:
数值型与序列型特征之间的联系:
我们可以将多个特征组合,然后通过一个简单的图来识别它们之间的关系。这种方法可以应用在数值型以及分类型(Pclass)的特征里,因为它们的值都是数值型。
我们可以通过以下代码来画出Pclass的柱状图:
grid = sns.FacetGrid(train_df, col=‘Survived‘, row=‘Pclass‘, size=2.2, aspect=1.6) grid.map(plt.hist, ‘Age‘, alpha=.5, bins=20) grid.add_legend() plt.show()
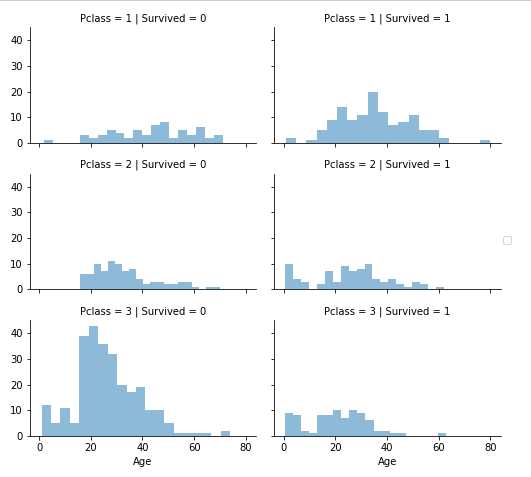
观察:
结论:
考虑将Pclass特征加入模型训练
离散型特征与Survived之间的联系:
现在我们可以查看离散型特征与survived之间的关系
我们可以通过以下方式将数据可视化:
grid = sns.FacetGrid(train_df, row=‘Embarked‘, size=2.2, aspect=1.6) grid.map(sns.pointplot, ‘Pclass‘, ‘Survived‘, ‘Sex‘,order=[1,2,3],hue_order=train_df.Sex.unique(),palette=‘deep‘) grid.add_legend() plt.show() #原作者代码没有加入order、hue_order因此图示会有错误,并得出了错误的结论,不过那个结论没有应用到后续的特征选择。。建议代码完成后结果可执行但是会提示有可能引起错误提示的话,还是修改下代码比较好
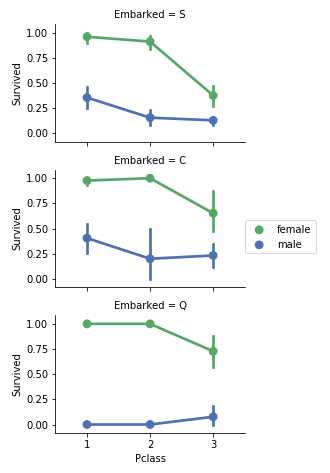
观察:
结论:
离散型特征与数值型特征之间的联系:
我们可能也想找出离散型与数值型特征之间的关系。
我们可以考虑查看Embarked(离散非数值型),Sex(离散非数值型),Fare(连续数值型)与Survived(离散数值型)之间的关系
grid = sns.FacetGrid(train_df, row=‘Embarked‘, col=‘Survived‘, size=2.2, aspect=1.6) grid.map(sns.barplot, ‘Sex‘, ‘Fare‘, order=train_df.Sex.unique(),alpha=.5, ci=None) grid.add_legend() plt.show()
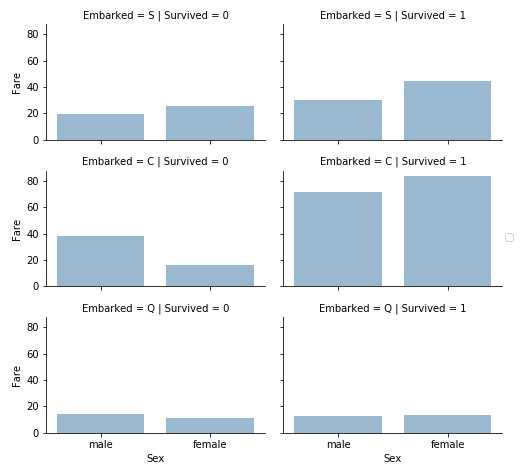
观察:
结论:
(10)加工数据
我们根据数据集以及题目的要求已经收集了一些假设与结论。到现在为止,我们暂时还没有对任何特征或数据进行处理。
接下来我们会根据之前做的假设与结论,以“修正数据”、“创造数据”以及“补全数据”为目标,对数据进行处理。
通过丢弃特征来修正数据:
这个步骤比较好的一个开始。通过丢弃某些特征,可以让我们处理更少的数据点,并让分析更简单。
根据我们之前的假设和结论,我
们希望丢弃Cabin和Ticket这两个特征。
在这里需要注意的是,为了保持数据的一致,我们需要同时将训练集与测试集里的这两个特征均丢弃。
具体步骤如下:
print("Before", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape)
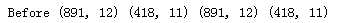
train_df = train_df.drop([‘Ticket‘, ‘Cabin‘], axis=1) test_df = test_df.drop([‘Ticket‘, ‘Cabin‘], axis=1) combine = [train_df, test_df] print(‘After‘, train_df.shape, test_df.shape, combine[0].shape, combine[1].shape)

通过已有的特征创建新特征:
我们在丢弃Name与PassengerId这两个特征之前,希望从Name特征里提取出Titles的特征,并测试Titles与survival之间的关系。
在下面的代码中,我们通过正则提取了Title特征,正则表达式为(\w+\.),它会在Name特征里匹配第一个以“.”号为结束的单词。同时,指定expand=False的参数会返回一个DataFrame。
for dataset in combine: dataset[‘Title‘] = dataset.Name.str.extract(‘([A-Za-z]+)\.‘, expand=False) pd.crosstab(train_df[‘Title‘], train_df[‘Sex‘]) #西方姓名中间会加入称呼,比如小男童会在名字中间加入Master,女性根据年龄段及婚姻状况不同也会使用Miss 或 Mrs 等,这算是基于业务的理解做的衍生特征,原作者应该是考虑可以用作区分人的特征因此在此尝试清洗数据后加入
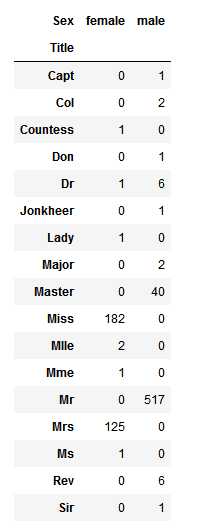
我们可以使用高一些更常见的名字或“Rare”来代替一些Title,如:
for dataset in combine: dataset[‘Title‘] = dataset[‘Title‘].replace([‘Lady‘, ‘Countess‘, ‘Capt‘, ‘Col‘, ‘Don‘, ‘Dr‘, ‘Major‘, ‘Rev‘, ‘Sir‘, ‘Jonkheer‘, ‘Dona‘], ‘Rare‘) dataset[‘Title‘] = dataset[‘Title‘].replace(‘Mlle‘, ‘Miss‘) dataset[‘Title‘] = dataset[‘Title‘].replace(‘Ms‘, ‘Miss‘) dataset[‘Title‘] = dataset[‘Title‘].replace(‘Mme‘, ‘Mrs‘) train_df[[‘Title‘, ‘Survived‘]].groupby([‘Title‘], as_index=False).mean()
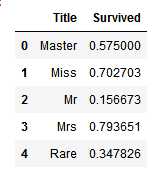
进一步的,我们可以将这些离散型的Title转换为有序的数值型:
title_mapping = {"Mr":1, "Miss":2, "Mrs":3, "Master":4, "Rare":5}
for dataset in combine:
dataset[‘Title‘] = dataset[‘Title‘].map(title_mapping)
dataset[‘Title‘] = dataset[‘Title‘].fillna(0)
train_df.head()
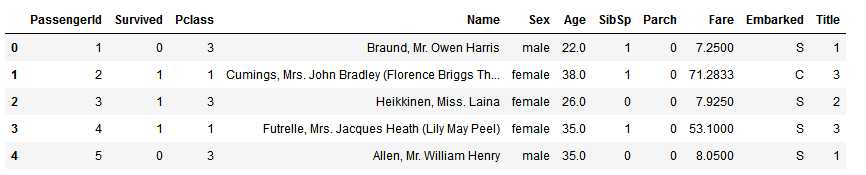
现在我们可以放心的从训练集与测试集里丢弃Name特征。同时,我们也不再需要训练集里的PassengerId特征:
train_df = train_df.drop([‘Name‘, ‘PassengerId‘], axis=1) test_df = test_df.drop([‘Name‘], axis=1) combine = [train_df, test_df] train_df.shape, test_df.shape
train_df.head()
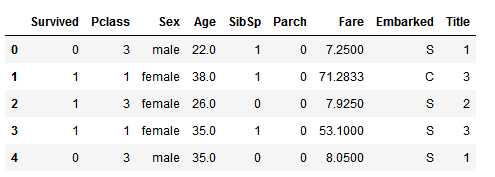
train_df[[‘Title‘, ‘Survived‘]].groupby([‘Title‘], as_index=False).mean()
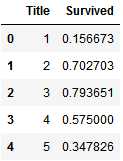
新的发现:
当我们画出Title,Age和Survived的图后,我们有了以下新的发现:
结论:
转换一个离散型的特征
现在我们可以将一些包含字符串数据的特征转换为数值型特征,因为在很多建模算法里,输入的参数要求为数值型。
这个步骤可以让我们达到补全数据的目标。
我们可以从转换Sex特征开始,将female转换为1,male转换为0。我们可以将新的特征命名为Gender:
for dataset in combine: dataset[‘Sex‘] = dataset[‘Sex‘].map({‘female‘:1, ‘male‘:0}).astype(int)
train_df.head()
补全连续数值型特征
现在我们可以开始为那些含null值或者丢失值的特征补全数据。我们首先会为Age特征补全数据。
现在我们总结一下三种补全连续数值型特征数据的方法:
1. 一个简单的方法是产生一个随机数,这个随机数的范围在这个特征的平均值以及标准差之间
2. 更精准的一个做法是使用与它相关的特征来做一个猜测。在这个案例中,我们发现Age,Gender和Pclass之间有关联。
所以我们会使用一系列Pclass和Gender特征组合后的中值,作为猜测的Age值。
所以我们会有一系列的猜测值如:当Pclass=1且Gender=0时,当Pclass=1且Gender=1时,等等…
3. 第三种方法是结合以上两种方法。我们可以根据一系列Pclass与Gender的组合,并使用第一种方法里提到的随机数来猜测缺失的Age值
方法1与方法3会在模型里引入随机噪音,多次的结果可能会有所不同。所以我们在这更倾向于使用方法2:
grid = sns.FacetGrid(train_df, row=‘Pclass‘, col=‘Sex‘, size=2.2, aspect=1.6) grid.map(plt.hist, ‘Age‘, alpha=.5, bins=20) grid.add_legend() plt.show()
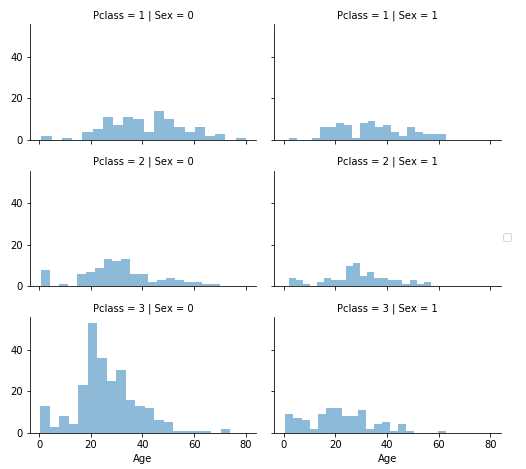
我们先准备一个空的数组来存储猜测的年龄,因为是Pclass与Gender的组合,所以数组大小为2x3:
guess_ages = np.zeros((2, 3))
然后我们可以对Sex(0或1)和Pclass(1,2,3)进行迭代,并计算出在6中组合下所得到的猜测(Age)值:
for dataset in combine: for i in range(0, 2): for j in range(0, 3): guess_df = dataset[(dataset[‘Sex‘] == i) & (dataset[‘Pclass‘] == j+1)][‘Age‘].dropna() age_guess = guess_df.median() # Convert random age float to nearest .5 age guess_ages[i, j] = int(age_guess / 0.5 + 0.5) * 0.5 for i in range(0, 2): for j in range(0, 3): dataset.loc[ (dataset.Age.isnull()) & (dataset.Sex == i) & (dataset.Pclass == j+1), ‘Age‘] = guess_ages[i,j] dataset[‘Age‘] = dataset[‘Age‘].astype(int) train_df.head()
现在我们对Age分段,并查看每段与Survived之间的相关性:
train_df[‘AgeBand‘] = pd.cut(train_df[‘Age‘], 5) train_df[[‘AgeBand‘, ‘Survived‘]].groupby([‘AgeBand‘], as_index=False).mean().sort_values(by=‘AgeBand‘, ascending=True)
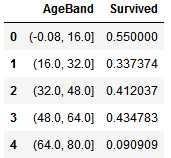
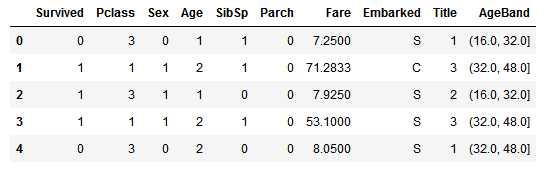
然后我们根据上面的分段,使用有序的数值来替换Age里的值:
for dataset in combine: dataset.loc[ dataset[‘Age‘] <= 16, ‘Age‘] = 0 dataset.loc[(dataset[‘Age‘] > 16) & (dataset[‘Age‘] <= 32), ‘Age‘] = 1 dataset.loc[(dataset[‘Age‘] > 32) & (dataset[‘Age‘] <= 48), ‘Age‘] = 2 dataset.loc[(dataset[‘Age‘] > 48) & (dataset[‘Age‘] <= 64), ‘Age‘] = 3 dataset.loc[ dataset[‘Age‘] > 64, ‘Age‘] train_df.head()
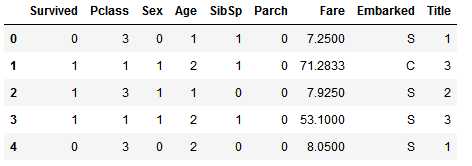
接着我们可以丢弃AgeBand特征:
train_df = train_df.drop([‘AgeBand‘], axis=1) combine = [train_df, test_df] train_df.head()
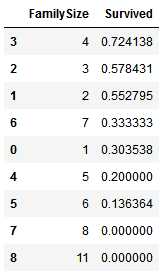
通过已有的特征组合出新特征
现在我们可以通过组合Parch和SibSp特征,创建一个新的FamilySize特征。这个步骤可以让我们从数据集里丢弃Parch与SibSp特征。
for dataset in combine: dataset[‘FamilySize‘] = dataset[‘SibSp‘] + dataset[‘Parch‘] + 1 train_df[[‘FamilySize‘, ‘Survived‘]].groupby([‘FamilySize‘], as_index=False).mean().sort_values(by=‘Survived‘, ascending=False)
接着我们可以创建另一个名为IsAlone的特征:
for dataset in combine: dataset[‘IsAlone‘] = 0 dataset.loc[dataset[‘FamilySize‘] == 1, ‘IsAlone‘] = 1 train_df[[‘IsAlone‘, ‘Survived‘]].groupby([‘IsAlone‘], as_index=False).mean()
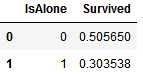
基于上面的数据表现,我们现在可以丢弃Parch、SibSp以及FamilySize的特征,保留IsAlone的特征:
train_df = train_df.drop([‘Parch‘, ‘SibSp‘, ‘FamilySize‘], axis=1) test_df = test_df.drop([‘Parch‘, ‘SibSp‘, ‘FamilySize‘], axis=1) combine = [train_df, test_df] train_df.head()
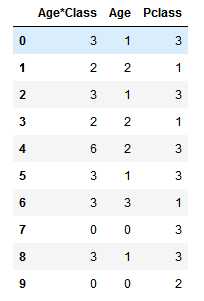
for dataset in combine: dataset[‘Age*Class‘] = dataset.Age * dataset.Pclass train_df.loc[:, [‘Age*Class‘, ‘Age‘, ‘Pclass‘]].head(10)
补全一个离散型的特征
Embarked特征主要有三个值,分别为S,Q,C,对应了三个登船港口。在训练集里,这个有2个缺失值,我们会使用频率最高的值来填充这个缺失值。
freq_port = train_df.Embarked.dropna().mode()[0]
freq_port
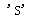
for dataset in combine: dataset[‘Embarked‘] = dataset[‘Embarked‘].fillna(freq_port) train_df[[‘Embarked‘, ‘Survived‘]].groupby([‘Embarked‘], as_index=False).mean().sort_values(by=‘Survived‘, ascending=False)
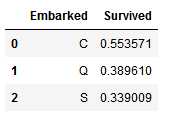
将离散型特征转换为数值型
我们现在可以将离散型的Embarked特征转换为数值型特征
for dataset in combine: dataset[‘Embarked‘] = dataset[‘Embarked‘].map({‘S‘: 0, ‘C‘: 1, ‘Q‘: 2}).astype(int) train_df.head()
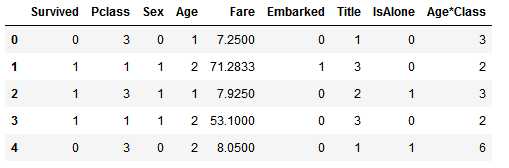
补全数值型特征
现在我们可以开始为测试集里的Fare特征补全数据。在补全时,我们可以使用最频繁出现的数据用于补全缺失值。
(我们也可以将Fare的数值做四舍五入,将它精确到2位)
test_df[‘Fare‘].fillna(test_df[‘Fare‘].dropna().median(), inplace=True) test_df.head()
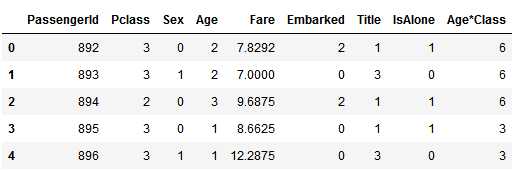
接下来我们将Fare分段:
train_df[‘FareBand‘] = pd.qcut(train_df[‘Fare‘], 4) train_df[[‘FareBand‘, ‘Survived‘]].groupby([‘FareBand‘], as_index=False).mean().sort_values(by=‘FareBand‘, ascending=True)
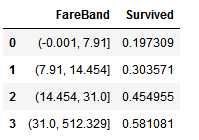
根据分段后的特征FareBand,将Fare转换为有序的数值型特征:
for dataset in combine: dataset.loc[ dataset[‘Fare‘] <= 7.91, ‘Fare‘] = 0 dataset.loc[(dataset[‘Fare‘] > 7.91) & (dataset[‘Fare‘] <= 14.454), ‘Fare‘] = 1 dataset.loc[(dataset[‘Fare‘] > 14.454) & (dataset[‘Fare‘] <= 31), ‘Fare‘] = 2 dataset.loc[dataset[‘Fare‘] > 31, ‘Fare‘] = 3 dataset[‘Fare‘] = dataset[‘Fare‘].astype(int) train_df = train_df.drop([‘FareBand‘], axis=1) combine = [train_df, test_df] train_df.head(10)
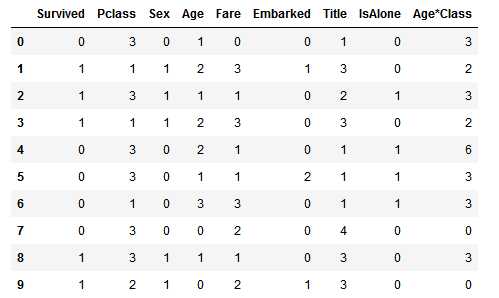
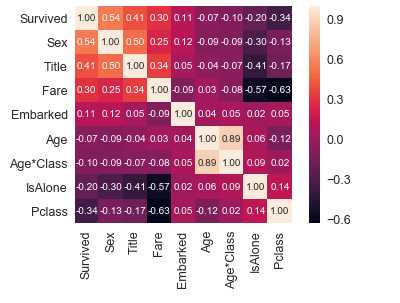
Survived与其他特征之间的相关性
corrmat = train_df.corr() k = 10 cols = corrmat.nlargest(k,‘Survived‘)[‘Survived‘].index #取出与Survived相关性最大的十项 cm = np.corrcoef(train_df[cols].values.T) #相关系数 sns.set(font_scale = 1.25) hm = sns.heatmap(cm,cbar = True,annot = True,square = True ,fmt = ‘.2f‘,annot_kws = {‘size‘: 10},yticklabels = cols.values,xticklabels = cols.values) plt.show()
(11)建模,预测,并解决问题
现在我们已经做好了训练模型的准备,在模型训练完后,我们即可将其应用到解决问题中。对于预测的问题,我们至少有60多种算法可供选择。
所以我们必须理解问题的类型和解决方案的需求,这样才能缩小模型的选择范围。现在这个问题是一个分类与回归的问题,
我们希望找出输出(即Survived)与其他特征(即Gender,Age,Port等)之间的关系。因为给定了训练集,所以这在机器学习里是一个有监督学习。
所以现在对算法的需求是:有监督学习加上分类与回归。根据这个条件,我们有以下模型可供选择:
现在我们将训练集与测试集再做一下区分:
X_train = train_df.drop(‘Survived‘, axis=1) Y_train = train_df[‘Survived‘] X_test = test_df.drop(‘PassengerId‘, axis=1).copy() X_train.shape, Y_train.shape, X_test.shape
Logistic Regression 是一个非常有用的模型,可以在工作流程里优先使用。它通过使用估计概率的方法衡量了离散型特征与其他特征之间的关系,是一个渐增型的逻辑分布。
logreg = LogisticRegression() logreg.fit(X_train, Y_train) Y_pred = logreg.predict(X_test) acc_log = round(logreg.score(X_train, Y_train) * 100, 2) acc_log #80.36
我们可以用Logistic Regression来验证我们之间做的假设与结论。这个可以通过计算特征值的系数来达成。正系数可以提升对数几率(所以增长了概率),负系数会降低对数几率(因此降低了概率):
coeff_df = pd.DataFrame(train_df.columns.delete(0)) coeff_df.columns = [‘Feature‘] coeff_df["Correlation"] = pd.Series(logreg.coef_[0]) coeff_df.sort_values(by=‘Correlation‘, ascending=False)
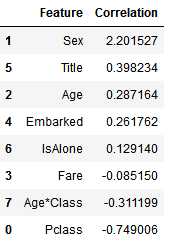
从上面的结果我们可以看出:
下一步我们使用SVM来分析数据并做分类与回归分析。
svc = SVC() svc.fit(X_train, Y_train) Y_pred = svc.predict(X_test) acc_svc = round(svc.score(X_train, Y_train) * 100, 2) acc_svc #83.84
可以看到使用SVM后的正确率得到了提升。
在模式识别中,KNN算法是一种非参数的方法,用于做分类与回归。使用KNN来分析此问题的话:
knn = KNeighborsClassifier(n_neighbors = 3) knn.fit(X_train, Y_train) Y_pred = knn.predict(X_test) acc_knn = round(knn.score(X_train, Y_train) * 100, 2) acc_knn #84.74
可以看到使用KNN的正确率比SVM更高
下面我们试试朴素贝叶斯:
gaussian = GaussianNB() gaussian.fit(X_train, Y_train) Y_pred = gaussian.predict(X_test) acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2) acc_gaussian #72.28
看来在这个问题中使用朴素贝叶斯不是一个很好的选择,从当前来看,它的正确率是最低的。
接下来我们试试 perceptron(感知机)算法,它可以用于二分类问题:
perceptron = Perceptron() perceptron.fit(X_train, Y_train) Y_pred = perceptron.predict(X_test) acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2) acc_perceptron #78.0
可以看到perceptron的正确率也不高
接下来试试Linear SVC:
linear_svc = LinearSVC() linear_svc.fit(X_train, Y_train) Y_pred = linear_svc.predict(X_test) acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2) acc_linear_svc #79.01
与随机梯度下降分类器:
sgd = SGDClassifier() sgd.fit(X_train, Y_train) Y_pred = sgd.predict(X_test) acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2) acc_sgd #69.92
接下来我们看看很常见的决策树算法:
decision_tree = DecisionTreeClassifier() decision_tree.fit(X_train, Y_train) Y_pred = decision_tree.predict(X_test) acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2) acc_decision_tree #86.76
可以看到,使用决策树的算法使得正确率达到了一个更高的值。在目前为止,它的正确率是最高的。
然后我们看看随机森林,随机森林通过组合多个决策树算法来完成:
random_forest = RandomForestClassifier(n_estimators=100) random_forest.fit(X_train, Y_train) Y_pred = random_forest.predict(X_test) acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2) acc_random_forest #86.76
通过比较模型的正确率,我们决定使用最高正确率的模型,即随机森林的输出作为结果提交。
(12)模型评价
models = pd.DataFrame({ ‘Model‘: [‘Support Vector Machines‘, ‘KNN‘, ‘Logistic Regression‘, ‘Random Forest‘, ‘Naive Bayes‘, ‘Perceptron‘, ‘Stochastic Gradient Decent‘, ‘Linear SVC‘, ‘Decision Tree‘], ‘Score‘: [acc_svc, acc_knn, acc_log, acc_random_forest, acc_gaussian, acc_perceptron, acc_sgd, acc_linear_svc, acc_decision_tree]}) models.sort_values(by=‘Score‘, ascending=False)
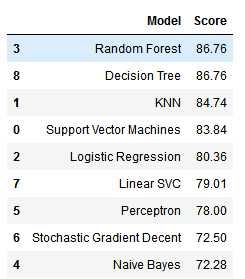
其中决策树与随机森林的正确率最高,但是我们在这里会选择随机森林算法,因为它相对于决策树来说,弥补了决策树有可能过拟合的问题。
最后我们做提交:
submission = pd.DataFrame({"PassengerId": test_df["PassengerId"], "Survived": Y_pred})
参考博文
http://www.cnblogs.com/zackstang/p/8185531.html
标签:提取 表达 uniq 基于 多少 class p12 net 等等
原文地址:https://www.cnblogs.com/rango-lhl/p/9686195.html