标签:tle 资料 步骤 实用 加权系数 replace 方向 enter 知识
https://blog.csdn.net/nieson2012/article/details/51980943
目录
?1.指数平滑定义及公式
?2.一次指数平滑
?3二次指数平滑
?4.三次指数平滑
?5指数平滑系数α的确定
1、指数平滑的定义及公式
产生背景:指数平滑由布朗提出、他认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续的未来,所以将较大的权数放在最近的资料。
基本原理:指数平滑法是移动平均法中的一种,其特点在于给过去的观测值不一样的权重,即较近期观测值的权数比较远期观测值的权数要大。根据平滑次数不同,指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权数,新数据给予较大的权数,旧数据给予较小的权数。
方法应用:指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。
指数平滑法的基本公式:St=a*yt+(1-a)*St-1 式中,
St--时间t的平滑值;
yt--时间t的实际值;
St-1--时间t-1的平滑值;
a--平滑常数,其取值范围为[0,1]
据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑和三次指数平滑法等。
2、一次指数平滑预测
当时间数列无明显的趋势变化,可用一次指数平滑预测。其预测公式为:
yt+1‘=a*yt+(1-a)*yt‘ 式中,
? yt+1‘--t+1期的预测值,即本期(t期)的平滑值St ;
? yt--t期的实际值;
? yt‘--t期的预测值,即上期的平滑值St-1 。
例题:已知某种产品最近15个月的销售量如下表所示:
用一次指数平滑值预测下个月的销售量y16。
为了分析加权系数a的不同取值的特点,分别取a=0.1,a=0.3,a=0.5计算一次指数平滑值,并设初始值为最早的三个数据的平均值,:以a = 0.5的一次指数平滑值计算为例,有
计算得到下表:
按上表可得 时间15月对应的19.9 26.2 28.1可以分别根据预测公式来预测第16个月的销售量。
以a = 0.5为例: y16=0.5*29+(1-0.5)*28.1=28.55(万台)
由上述例题可得结论
1)指数平滑法对实际序列具有平滑作用,权系数(平滑系数)a 越小,平滑作用越强,但对实际数据的变动反应较迟缓。
2)在实际序列的线性变动部分,指数平滑值序列出现一定的滞后偏差的程度随着权系数(平滑系数)a 的增大而减少,但当时间序列的变动出现直线趋势时,用一次指数平滑法来进行预测仍将存在着明显的滞后偏差。因此,也需要进行修正。修正的方法也是在一次指数平滑的基础上再进行二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型,故称为二次指数平滑法。
3、二次指数平滑预测
1) a为加权系数;
2) 指数平滑法对实际序列具有平滑作用,权系数(平滑系数)越小,平滑作用越强,但是对实际数据的变动反映较迟缓;
3) 在实际序列的线性变动部分,指数平滑值序列出现一定的滞后偏差的程度随着权系数(平滑系数)的增大而减少;但当时间序列的变动出现直线趋势时,用一次指数平滑法来进行预测仍将存在着明显的滞后偏差。因此,也需要进行修正。
4) 修正的方法也是在一次指数平滑的基础上再进行二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型,故称为二次指数平滑法。
在一次指数平滑的基础上得二次指数平滑 的计算公式为:
? 式中: St(2)——第t周期的二次指数平滑值;
? St(1)——第t周期的一次指数平滑值;
? St-1(2)——第t-1周期的二次指数平滑值;
? a ——加权系数(也称为平滑系数)。
二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。它不能单独地进行预测,必须与一次指数平滑法配合,建立预测的数学模型,然后运用数学模型确定预测值。
二次指数平滑数学模型:
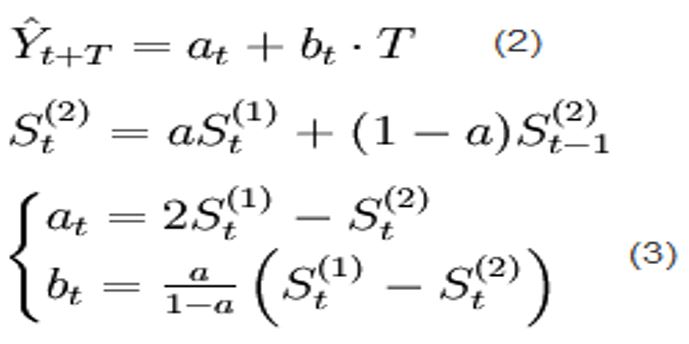
例题2:某地1983年至1993年财政入的资料如下,试用指数平滑法求解趋势直线方程并预测1996年的财政收入
例3:已知某厂1978~1998年的钢产量如下表所示,试预测1999年、2000年该厂的钢产量。(用excel如何实现平滑指数)
下面利用指数平滑工具进行预测,具体步骤如下:
选择工具菜单中的数据—数据分析命令,此时弹出数据分析对话框。
在分析工具列表框中,选择指数平滑工具。
这时将出现指数平滑对话框,如图所示:
一次指数平滑设置及输出
二次指数平滑设置及输出
最终结果输出及计算
根据二次平滑指数数学模型进行计算a、b值。
得到趋势线预测模型:y=3994.9+141.2T,从而可以计算出:
y1999=3994.9+141.2*1=4136.14
y2000=3994.9+141.2*2= 4277.34
4、三次指数平滑预测
若时间序列的变动呈现出二次曲线趋势,则需要采用三次指数平滑法进行预测。三次指数平滑是在二次指数平滑的基础上再进行一次平滑,其计算公式为:
三次指数平滑法的预测模型为:
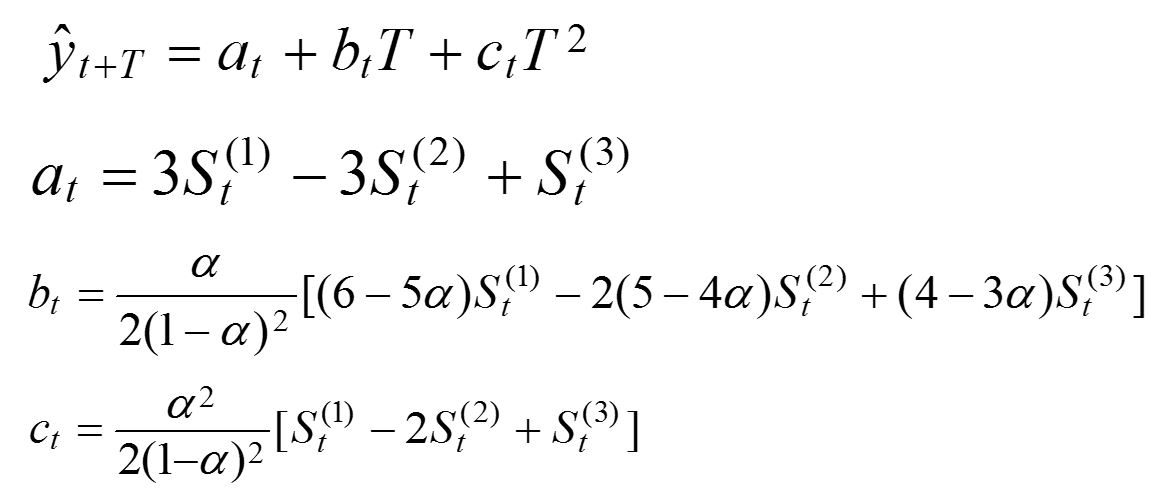
例4:我国某种耐用消费品1996年至2006年的销售量如表所示,试预测2007、2008年的销售量。
三次指数平滑的计算表:
解:通过实际数据序列呈非线性递增趋势,采用三次指数平滑预测方法。解题步骤如下。确定指数平滑的初始值和权系数(平滑系数)a。设一次、二次指数平滑的初始值为最早三个数据的平均值,即
实际数据序列的倾向性变动较明显,权系数(平滑系数)a 不宜取太小,故取a= 0.3。
根据指数平滑值计算公式依次计算一次、二次、三次指数平滑值:
计算非线性预测模型的系数at,bt,ct。目前周期数t = 11,将表1.6中的有关数据代入式(1-19)、式(1-20)、式(1-21)后分别得
建立非线性预测模型。将各系数代入式(1-18)得
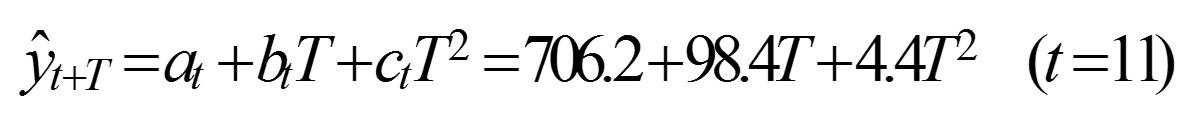
预测2007年和2008年的产品销售量。2007年,其预测超前周期为T = 1;2008年,其预测超前周期为T = 2。代入模型,得预测2007年和2008年的产品销售量。2007年,其预测超前周期为T= 1;2008年,其预测超前周期为T= 2。代入模型,得
于是得到2007年的产品销售量的预测值为809万台,2008年的产品销售量的预测值为920万台。预测人员可以根据市场需求因素的变动情况,对上述预测结果进行评价和修正。
5、加权系数a的选择
在指数平滑法中,预测成功的关键是a的选择。a的大小规定了在新预测值中新数据和原预测值所占的比例。a值愈大,新数据所占的比重就愈大,原预测值所占比重就愈小,反之亦然。
指数平滑法的缺点:
? (1)对数据的转折点缺乏鉴别能力,但这一点可通过调查预测法或专家预测法加以弥补。
? (2)长期预测的效果较差,故多用于短期预测。
指数平滑法的优点:
? (1)对不同时间的数据的非等权处理较符合实际情况。
? (2)实用中仅需选择一个模型参数a 即可进行预测,简便易行。
? (3)具有适应性,也就是说预测模型能自动识别数据模式的变化而加以调整。
欢迎关注微信公众号,与您分享更多精彩内容!
--------------------- 本文来自 夜空骑士 的CSDN 博客 ,全文地址请点击:https://blog.csdn.net/nieson2012/article/details/51980943?utm_source=copy
标签:tle 资料 步骤 实用 加权系数 replace 方向 enter 知识
原文地址:https://www.cnblogs.com/DjangoBlog/p/9702376.html