匈牙利算法

标签：说明   遍历   代码实现   color   基于   memset   cow   循环   匹配   

0 - 相关概念

0.1 - 匈牙利算法

　　匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是二部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

0.2 - 二分图

　　若图$G$的结点集合$V(G)$可以分成两个非空子集$V_1$和$V_2$，并且图$G$的任意边$xy$关联的两个结点$x$和$y$分别属于这两个子集，则$G$是二分图。

1 - 基本思想

1. 找到当前结点$a$可以匹配的对象$A$，若该对象$A$已被匹配，则转入第3步，否则转入第2步
2. 将该对象$A$的匹配对象记为当前对象$a$，转入第6步
3. 寻找该对象$A$已经匹配的对象$b$，寻求其$b$是否可以匹配另外的对象$B$，如果可以，转入第4步，否则，转入第5步
4. 将匹配对象$b$更新为另一个对象$B$，将对象$A$的匹配对象更新为$a$，转入第6步
5. 结点$a$寻求下一个可以匹配的对象，如果存在，则转入第1步，否则说明当前结点$a$没有可以匹配的对象，转入第6步
6. 转入下一结点再转入第1步

2 - 样例解析

　　上面的基本思想看完肯定一头雾水（很大程度是受限于我的表达能力），下面通过POJ 1274来就匈牙利算法做一个详细的样例解析。

2.1 - 题目大意

　　农场主John有$N$头奶牛和$M$个畜栏，每一头奶牛需要在特定的畜栏才能产奶。第一行给出$N$和$M$，接下来$N$行每行代表对应编号的奶牛，每行的第一个数值$T$表示该奶牛可以在多少个畜栏产奶，而后的$T$个数值为对应畜栏的编号，最后输出一行，表示最多可以让多少头奶牛产奶。

2.1 - 输入样例

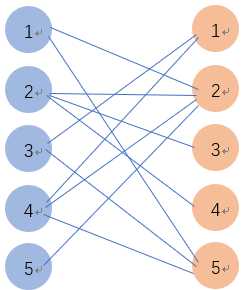
5 5
2 2 5
3 2 3 4
2 1 5
3 1 2 5
1 2

2.2 - 匈牙利算法解题思路

2.2.1 - 构造二分图

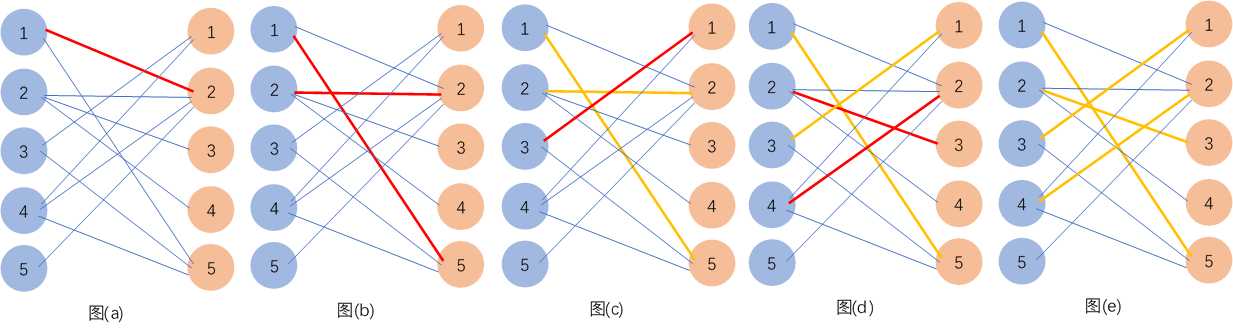
　　根据输入样例构造如下二分图，蓝色结点表示奶牛，黄色结点表示畜栏，连线表示对应奶牛能在对应畜栏产奶。

2.2.2 - 模拟算法流程

• 为结点1（奶牛）分配畜栏，分配畜栏2（如图(a)加粗红边所示）
• 为结点2（奶牛）分配畜栏，由于畜栏2已经被分配给结点1（奶牛），所以寻求结点1（奶牛）是否能够分配别的畜栏，以把畜栏2腾给结点2（奶牛）。结点2（奶牛）在畜栏5也可以产奶，因此，给结点1（奶牛）分配畜栏5（如图(b)加粗黄边所示），然后把畜栏2给结点2（奶牛）（如图(b)加粗红边所示）
• 为结点3（奶牛）分配畜栏，分配畜栏1（如图(c)加粗红边所示）
• 为结点4（奶牛）分配畜栏，由于畜栏1已经被分配给结点3（奶牛），所以寻求结点3（奶牛）是否能够分配别的畜栏，但下一个可以分配给结点3（奶牛）的畜栏5已经被分配给结点1（奶牛），因此寻求结点1（奶牛）是否能够分配别的畜栏，发现已经没有畜栏可以分配，因此结点4（奶牛）不能给其分配畜栏1，转而寻求下一个可以分配的畜栏2，畜栏2已经分配给结点2（奶牛），寻求结点2（奶牛）可否能够分配其它畜栏，发现畜栏3可以分配给结点2（奶牛）（如图(d)加粗红边所示），再把畜栏2分配给结点4（奶牛）（如图(d)加粗红边所示）
• 为结点5（奶牛）分配畜栏，由于畜栏2已经分配给结点4（奶牛），且结点4（奶牛）没有其它可以分配给它的畜畜栏了，而结点5（奶牛）也没有其它可以分配给它的畜栏，因此结点5（奶牛）没有畜栏可分配
• 最多有4头奶牛（编号为1、2、3、4的奶牛）分配到了畜栏（如图(e)加粗黄边所示）

 2.2.3 - 代码实现

// 导入相关库
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

// 定义需要的变量
#define N 205 
#define M 205

bool line[N][M]; //表示对应位置的奶牛和畜栏是否有边
int hascow[M]; //表示对应位置的畜栏被分配到哪一只编号的奶牛（0是未分配）
bool used[M]; //表示对应位置的畜栏是否已经被走过了，用于确保寻求增广路不走重复结点
int n, m;

//分配
bool find(int x) {
    for (int i=1; i<=m; i++) { //遍历所有畜栏
        //如果该奶牛可以分配到这个畜栏并且该畜栏未被使用
        if (line[x][i] && !used[i]) {
            used[i] = true; //标记该畜栏当前循环被使用了
            //如果该畜栏没有被分配或者可以通过给原本占有该畜栏的奶牛分配其它畜栏
            if (!hascow[i] || find(hascow[i])) { 
                //将该畜栏分配给该奶牛
                hascow[i] = x;
                return true; //分配成功
            }
        }
    }
    return false; //分配失败
}            

int main() {
    int t, x, res;
    while (~scanf("%d%d", &n, &m)) {
　　　　 //初始化变量，然后根据输入格式构建二分图
        memset(line, 0, sizeof(line));
        for (int i=1; i<=n; i++) {
            scanf("%d", &t);
            for (int j=1; j<=t; j++) {
                scanf("%d", &x);
                line[i][x] = true;
            }    
        }
        res = 0;
        memset(hascow, 0, sizeof(hascow));
        for (int i=1; i<=n; i++) {
            memset(used, 0, sizeof(used));
            if (find(i)) res ++; //如果可以成功给该奶牛分配畜栏，可以分配的奶牛数量+1
        }
        printf("%d\n", res);
    }
    return 0;
}

https://blog.csdn.net/tanzhangwen/article/details/8262006

https://vjudge.net/problem/10500/origin

https://www.cnblogs.com/qq-star/p/4633101.html

匈牙利算法

标签：说明   遍历   代码实现   color   基于   memset   cow   循环   匹配   

原文地址：https://www.cnblogs.com/CZiFan/p/9708746.html