标签:后缀表达式 ges desktop 提交 osi port 优先 成员 user
项目成员:梁华超、林贤杰
项目仓库:Github
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 25 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 25 |
| Development | 开发 | 1200 | 1740 |
| · Analysis | · 需求分析 (包括学习新技术) | 40 | 55 |
| · Design Spec | · 生成设计文档 | 40 | 41 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 31 |
| · Design | · 具体设计 | 40 | 66 |
| · Coding | · 具体编码 | 1100 | 1520 |
| · Code Review | · 代码复审 | 40 | 41 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 64 |
| Reporting | 报告 | 70 | 100 |
| · Test Report | · 测试报告 | 20 | 24 |
| · Size Measurement | · 计算工作量 | 20 | 21 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 58 |
| 合计 | 1390 | 1963 |
项目文件结构如下:
| 模块 | 功能 |
|---|---|
| main.py | 主函数 |
| answer.py | 计算答案和校对答案 |
| exp_generate.py | 表达式生成 |
| remove_dulicate.py | 题目判重 |
| suffix_expression.py | 将中缀表达式转成后缀表达式和求值 |
本设计涉及到的基本数据类型和表达式有栈,二叉树,逆波兰表达式(后缀表达式)
表达式生成 :
仔细分析表达式有如下特点:
利用python中字符串列表来存储四则表达式,新建一个列表,大小为运算符个数+运算数,然后循环遍历此列表,在偶数位置插入随机的运算数,在奇数位置插入随机的运算符。
括号的插入:
左括号的插入位置是从0到操作数个数的一半之间的一个随机数,右边括号为左括号的位置+1到操作数个数的一半+1。
计算答案:
将中缀表达式转为后缀表达式,再进行求值
题目判重:
将中缀表达式转为后缀表达式,最后转为二叉树,对转换得到的二叉树的左右子树进行自定义排序,最后生成一个字符串,比较2个表达式生成的这个序列,如果一样,则说明这两个式子是重复的。
生成的二叉树如下这样:

需要注意的是除号后面的运算符不能为0,如果生成的是0,即重新生成插入,直到生成不为0的运算符为止。
while i < exp_num: random_num_operation = randint(1, config.max_num_of_oper) is_need_parenteses = randint(0,1) number_of_oprand = random_num_operation + 1 #操作数比操作符的数目多1 exp = [] for j in range(random_num_operation + number_of_oprand): if j % 2 == 0: #随机生成操作数 exp.append(self.generate_operand(randint(0,3), config.num_range)) if j > 1 and exp[j-1] == ‘÷‘ and exp[j] == ‘0‘: while True: exp[j-1] = self.generate_operation() if exp [j-1] == ‘÷‘: continue else: break else: #生成运算符 exp.append(self.generate_operation()) #判断是否要括号 if is_need_parenteses and number_of_oprand != 2: expression = " ".join(self.generate_parentheses(exp, number_of_oprand)) else: expression = " ".join(exp) #判断是否有重复 if self.is_repeat(exp_list, expression) or suffix_to_value(to_suffix(expression)) == False: continue else: exp_list.append(expression) i = i + 1
如果生成的括号表达式形如 (1 + 2/3 + 3),则认为是没有意义的括号,需要重新插入。
if exp: exp_length = len(exp) left_position = randint(0,int(num/2)) right_position = randint(left_position+1, int(num/2)+1) mark = -1 for i in range(exp_length): if exp[i] in [‘+‘, ‘-‘, ‘x‘, ‘÷‘]: expression.append(exp[i]) else: mark += 1 if mark == left_position: expression.append(‘(‘) expression.append(exp[i]) elif mark == right_position: expression.append(exp[i]) expression.append(‘)‘) else: expression.append(exp[i]) #如果生成的括号表达式形如 (1 + 2/3 + 3) 则重新生成 if expression[0] == ‘(‘ and expression[-1] ==‘)‘: expression = self.generate_parentheses(exp, number_of_oprand) return expression
初始化两个栈,分为运算符栈和后缀表达式栈,遍历表达式列表,如果遇到运算符:
a. 如果运算符栈为空,则直接入栈
b. 如果运算符栈不为空,则取出栈顶top元素
如果栈顶top元素是左括号或者算术优先级高于栈顶top元素,那么就直接入栈
如果遇到左括号:
左括号直接入运算符栈
如果遇到右括号:
如果运算符栈不为空,那么直接出栈,添加到后缀表达式栈,直到遇到左括号
suffix_stack = [] #后缀表达式结果 ops_stack = [] #操作符栈 infix = exp.split(‘ ‘) #print(infix) for item in infix: if item in [‘+‘, ‘-‘, ‘x‘, ‘÷‘]: #遇到运算符 while len(ops_stack) >= 0: if len(ops_stack) == 0: ops_stack.append(item) break op = ops_stack.pop() if op == ‘(‘ or ops_rule[item] > ops_rule[op]: ops_stack.append(op) ops_stack.append(item) break else: suffix_stack.append(op) elif item == ‘(‘: # 左括号直接入栈 ops_stack.append(item) elif item == ‘)‘: #右括号 while len(ops_stack) > 0: op = ops_stack.pop() if op == "(": break else: suffix_stack.append(op) else: suffix_stack.append(item) # 数值直接入栈 while len(ops_stack) > 0: suffix_stack.append(ops_stack.pop())
import operator import suffix_expression ? class Node: """ 二叉树的结点 """ def __init__(self, value): self.value = value self.left = None self.right = None ? def generate_binary_tree(exp): """ 生成二叉树 """ tree_stack = [] for item in exp: #print(item) parent = Node(item) if not item in [‘+‘, ‘-‘, ‘x‘, ‘÷‘]: #操作数 tree_stack.append(parent) else: #运算符 right = tree_stack.pop() left = tree_stack.pop() parent.right = right parent.left = left tree_stack.append(parent) #二叉树的根 parent = tree_stack[-1] return parent ? def tree_is_same(root): """ 判断二叉树是否相同 """ if not root.left: if not root.right: return root.value elif root.value == ‘+‘ or root.value == ‘x‘: left = tree_is_same(root.left) right = tree_is_same(root.right) if operator.le(left, right): #print(root.value + left + right) return root.value + left + right else: return root.value + right + left else: return root.value + tree_is_same(root.left) + tree_is_same(root.right)
文件说明:
| 文件 | 说明 |
|---|---|
| Answer.txt | 生成表达式答案文件 |
| Exercises.txt | 生成表达式存储的文件 |
| Grade.txt | 题目对错数量统计文件 |
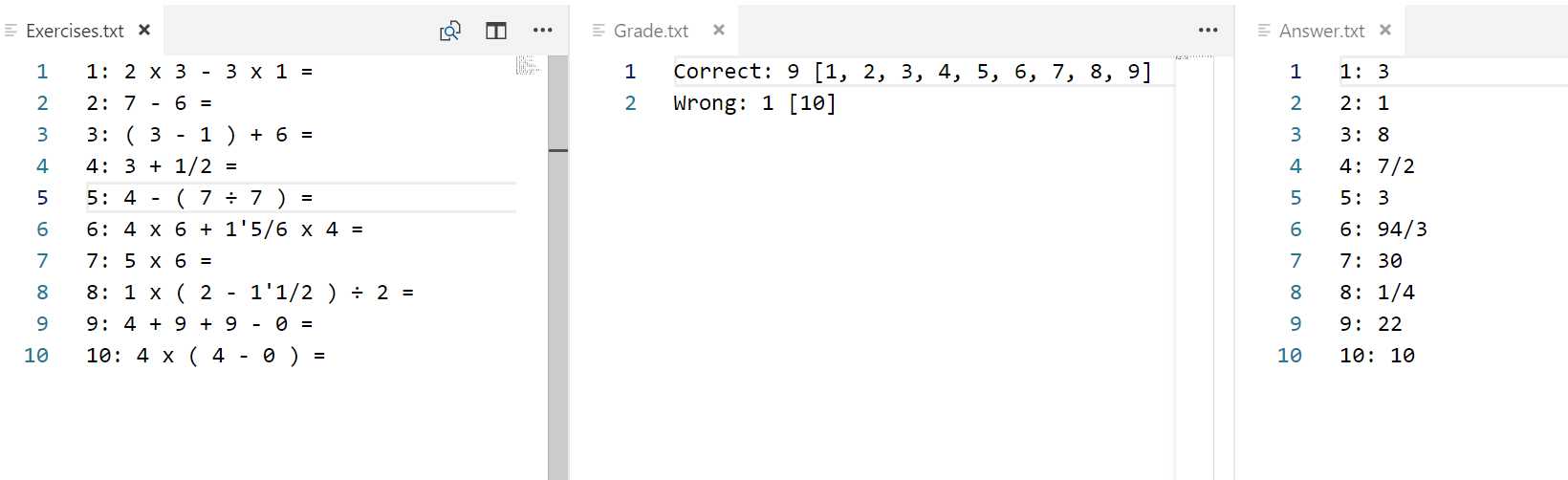
结果:
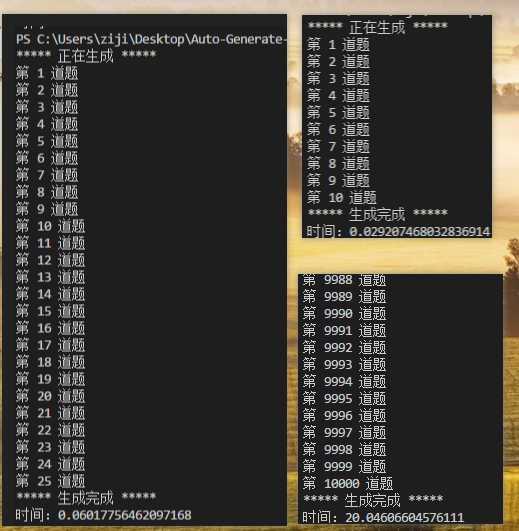
效能分析:
标签:后缀表达式 ges desktop 提交 osi port 优先 成员 user
原文地址:https://www.cnblogs.com/tworld/p/9709610.html