标签:问题 1.2 距离 变量 线框图 最简 圆心 大小 基础
第四讲 消隐算法
一、消隐
消隐:(消除二义性)就是必须在绘制时消除被遮挡的不可见的线或面,习惯上称作消除隐藏线和隐藏面;
消隐不仅与消隐对象有关还与观察者的位置有关。
1.1消隐的分类
1.1.1按消隐对象分类
(1)线消隐:消隐对象是物体上的边,消除的是物体上不可见的边。
(2)面消隐:消隐对象是物体上的面,消除的是物体上不可见的面,通常做【真实感图形】消隐时用面消隐。
1.1.2按消隐空间分类
(1)物体空间消隐算法:以场景中的【物体】为处理单元,假设场景中有k个物体,将其中一个物体与其余k-1个物体逐一比较,仅显示它可见表面以达到消隐的目的,通常用于【线框图】的消隐。
1.Roberts算法:要求所有被显示的物体都是凸的,对于凹体要先分割成多个凸体的组合。【计算量甚大】
2.光线投射法:一条视线与场景中的物体可能有许多交点,求出这些交点后需要排序,在前面的才能被看到。
光线投射:是求光线(视线,如视点与象素连成的线)与场景的交点。
(2)图像空间消隐算法:以屏幕窗口内的每个【象素】为处理单元。确定在每一个象素处,场景中的k个物体哪一个距离观察点【最近】,从而用它的颜色来显示该象素。【消隐算法的主流】
画家算法:要做到去除隐藏面的最简单的方法。如果一个场景中有许多物体,就是先画远的东西,再画近的东西。这样一来,近的东西自然就会盖住远的东西。
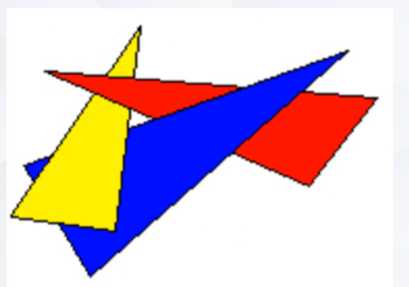
这张图片由于三个部分互相叠加,无法判断谁最远谁最近,所以用画家算法就无法解决。
——>画家算法只能解决【简单场景】的消隐问题。
1.Z-buffer算法(深度缓冲器算法)
帧缓冲器对应数组:intensity(x,y)——>属性数组(帧缓冲器)
存储图像每个空间可见象素的光强或颜色
深度缓冲器对应数组:depth(x,y)——>深度数组(z-buffer)
存放图像空间每个可见象素的z坐标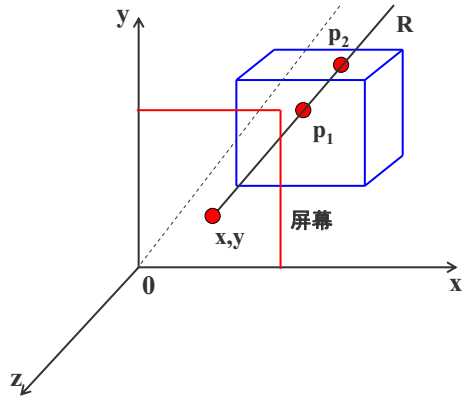
假设xoy面为投影面,z轴为观察方向,过屏幕上任意象素点(x,y)做平行于z轴的射线R,与物体表面相交于p1,p2点,p1和p2点的z值称为该点的深度值,z-buffer算法比较p1和p2的z值,将最大的z值存入z缓冲器中,显然屏幕上(x,y)显示p1点的颜色。
【算法思想】
先将Z缓冲器中各单元的初始值置为最小值,当要改变某个象素的颜色值时,首先检查当前多边形的深度值是否大于该象素原来的深度值(保存在该象素所对应的Z缓冲器的单元中),如果大于原来的Z值,说明当前多边形更靠近观察点,用它的颜色替换原象素的颜色。
【优点】
(1)Z-buffer算法比较简单,直观;
(2)在象素上以近物取代远物,与物体在屏幕上的出现顺序无关,有利于硬件实现。
【缺点】
(1)占用空间大;
(2)没有利用图形的相关性与连续性;
(3)该算法是在象素级上的消隐算法。
对缺点进行改进:
【1>并不需要开辟一个与图像大小相等的深度缓存数组,只用一个深度缓存变量zb的改进算法】
【关键问题】
1.判断象素点(i,j)是否在pk的投影多边形之内,不是一件容易的事,节省了空间但牺牲了时间。
2.计算多边形pk在点(i,j)处的深度。设多边形pk的平面方程
【点与多边形的包含性检测】
(1)射线法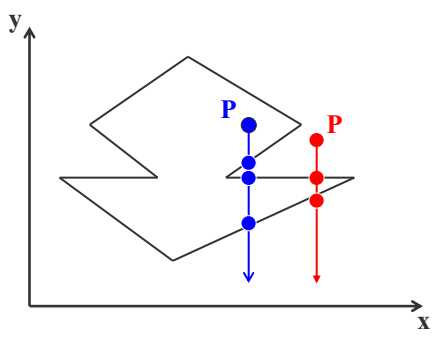
由被检测点p处向y=负无穷方向作射线,交点个数为奇数,则被检测点在多边形内部,交点个数为偶数表示在多边形外部。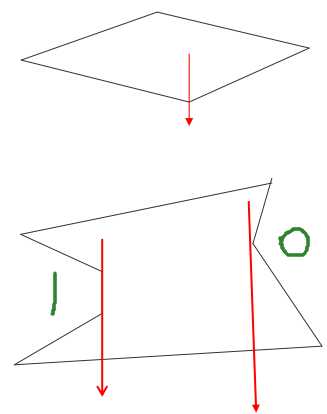
若射线正好经过多边形的顶点, 则采用“左开右闭”的原则来实现,也就是,当射线与某条边的顶点相交时,若边在射线的左侧,交点有效,计数,若边在射线的右侧交点无效,不计数。
【射线法弊端】
1.计算量大
2.不稳定
(2)弧长法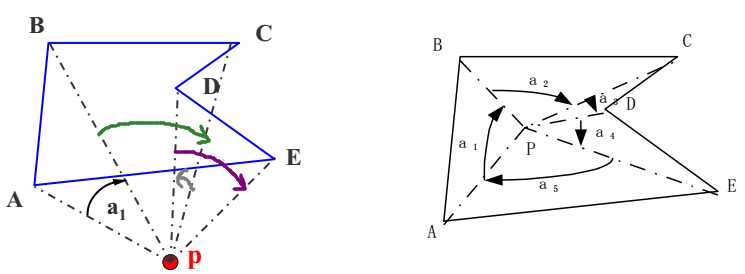
以p点为圆心,作单位圆,把边投影到单位圆上,对应一段段弧长,规定逆时针为正,顺时针为负,计算弧长代数和。
代数和为0,点在多边形外部;
代数和为2π,点在多边形内部;
代数和为π,点在多边形边上。
【稳定——>假如算出来代数和不是0,而是0.2、0.1,那么基本上可以断定这个点在外部,可以认为是计算误差引起的,实际上是0】
【效率不高——>弧长并不容易求】
(3)以顶点符号为基础的弧长累加方法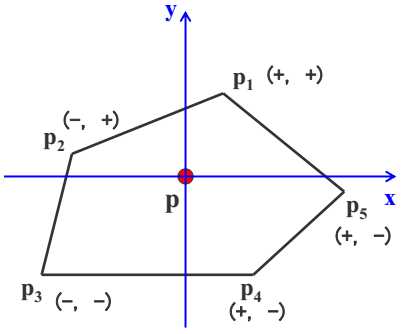
p是被测点,按照弧长法,p点的代数和为2π,现在,不计算角度,以如下规定取代原来的弧长计算
同一个象限认为是0,跨过一个象限是π/2,跨过两个象限是π。
标签:问题 1.2 距离 变量 线框图 最简 圆心 大小 基础
原文地址:https://www.cnblogs.com/Penglimei/p/9708052.html