KMP算法总结

标签：int   --   div   时间复杂度   复杂度   ++   基于   color   char   

【KMP简述】

 主串长度为n,模式串长度为m，朴素的算法下，对于主串S的每一位S[i]都要往后扫描m个字符，所以时间复杂度为O（nm）。

对于KMP算法，它的时间复杂度降到了O（m+n）。原理是用一个next数组预处理了主串的局部匹配信息（最长相同前后缀长度），在进行主串与模式串的匹配时，保证了主串一直往后遍历不回溯，仅改变指向模式串的指针位置。

【算法原理详解】

来看这样一个例子，

主串A B C A B C A C A A B,

模式串A B C A C

 很显然这次匹配在第4位发生失配，主串指针和模式串指针指向4，根据KMP算法特点，主串指针继续往后不回溯，应为5，那么此时模式串的指针位置应该从4变到几呢？

注意到这样一个事实，在第i位发生失配，则i之前的串一定是匹配的，在这个例子中ABCA是匹配的，注意到next数组的定义：next[i]表示i之前的串最长相同前后缀长度

可以知道，在进行下一次匹配（i=5时），则可以把模式串的指针跳到next[i]。很显然next[5] = 2 （就是AB）

为什么呢因为主串前缀AB和主串后缀AB相同，主串前缀AB和模式串前缀AB已经匹配，则必然主串后缀AB与模式串前缀AB必然相同，所以可以直接跳过直接匹配，直接匹配模式串下一个字符（也就是第2个字符）即可。

【next数组求法】

一个关键的问题就是，如何快速地预处理出基于主串的next数组。

主串A B C A B C B 7C A A B,

模式串A B C A C

考虑到一个动态规划的想法，如果我们已经求出了next[i] = k,那么在求next[i+1]时是怎那样的呢？

比如已经求出了next[5] = 2，在求next[6]时，很显然根据next[5]我们已经知道了第0,1位和第3,4位已经是之前的最大相同前后缀了，那么如果第2位和第5位还相同的话,即str[2] = str[5]

则next[6] = next[5] + 1 = 3

即str[k] = str[i]时，next[i+1] = next[i] + 1, i，k增加1继续匹配之后的next[i]

如果不相同呢？即str[k] != str[i]. 我们也不必重新一个一个匹配。例如求next[7] ，已经求出next[i] = next[6] = 3， k = 3， str[k] ！= str[i]，只需要令k = next[k] = 0,然后继续比较str[0] = str[6]，然后还不相等，此时k = next[0] = -1(把next[0]置为-1就是为了标志这种情况)，这是就知道next[7] = 0了。

即str[k] != str[i]时，k = next[k]，i不动，继续匹配直到str[k] = str[i]或者next[k]=-1。

以下图片摘自：https://www.cnblogs.com/yjiyjige/p/3263858.html

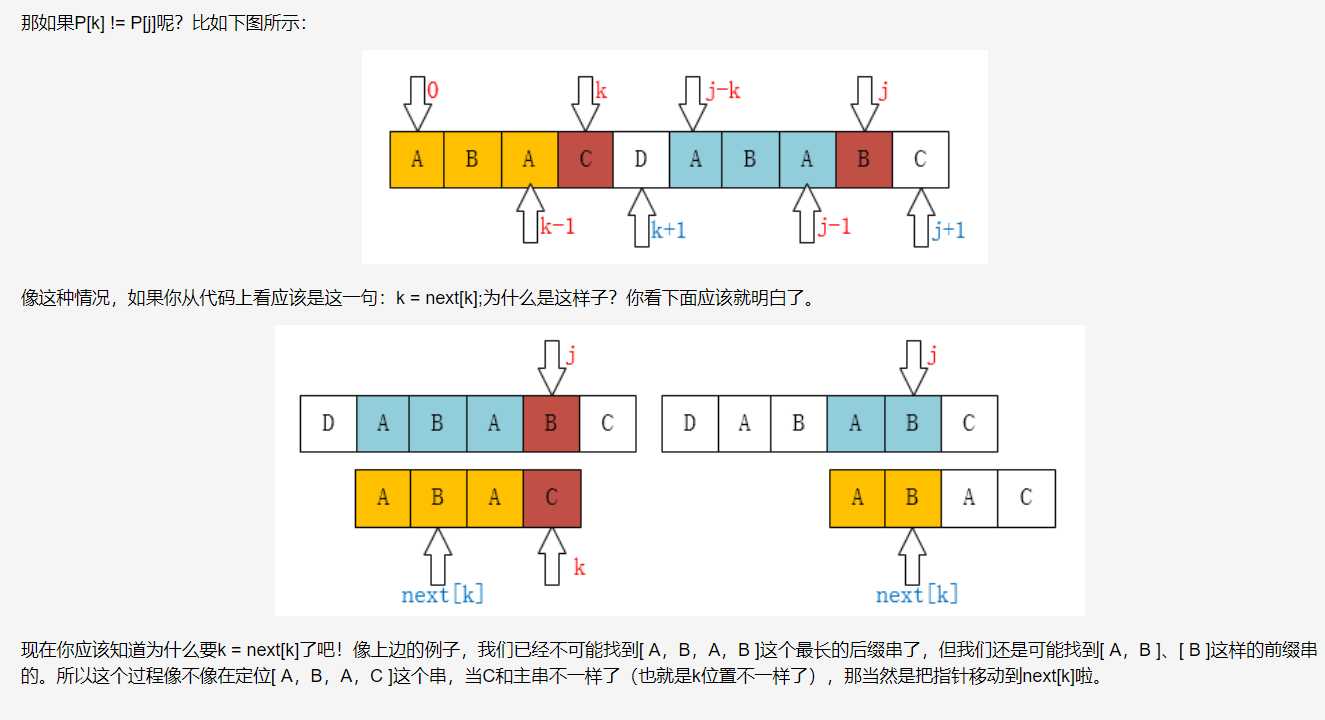
【模板】

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1000002;
int next[N];
char S[N], T[N];
int slen, tlen;

void getNext()
{
    int j, k;
    j = 0; k = -1; next[0] = -1;
    while(j < tlen)
        if(k == -1 || T[j] == T[k])
            next[++j] = ++k;
        else
            k = next[k];

}
/*
返回模式串T在主串S中首次出现的位置
返回的位置是从0开始的。
若返回-1则没有找到匹配
*/
int KMP()
{
    int i = 0, j = 0;
    getNext();

    while(i < slen && j < tlen)
    {
        if(j == -1 || S[i] == T[j])
        {
            i++; j++;
        }
        else
            j = next[j];
    }
    if(j == tlen)
        return i - tlen;
    else
        return -1;
}
/*
返回模式串在主串S中出现的次数
*/
int KMP_Count()
{
    int ans = 0;
    int i, j = 0;
    getNext();
    for(i = 0; i < slen; i++)
    {
        while(j > 0 && S[i] != T[j])
            j = next[j];
        if(S[i] == T[j])
            j++;
        if(j == tlen)
        {
            ans++;
            j = next[j];
        }
    }
    return ans;
}

int main()
{
    
    int TT;
    int i, cc;
    cin>>TT;
    while(TT--)
    {
        cin>>S>>T;
        slen = strlen(S);
        tlen = strlen(T);
        cout<<"模式串T在主串S中首次出现的位置: "<<KMP()<<endl;
        cout<<"模式串T在主串S中出现的次数: "<<KMP_Count()<<endl;
    }
    return 0;
}

KMP算法总结

标签：int   --   div   时间复杂度   复杂度   ++   基于   color   char   

原文地址：https://www.cnblogs.com/czsharecode/p/9703684.html