标签:weight 结束 数通 迭代思想 实现 局部变量 空间 简单的 创建
FUNCTION RETURN
function 函数名 (形参1,形参2,.... ){
//函数体(代码块)
}
本质上就是使用一个名字来达到执行其中函数中的代码的作用。通常可以分两种情形的调用:
第一种:没有返回值的函数,则调用语句是独立语句:
函数名(实参1,实参2, .... ); //实参个数应该跟形参有匹配性。
第二种:有返回值的函数,则调用语句,通常会“混杂”在别的语句中,并将要将该调用语句当作一个“数据”来使用:
A: $v1 = 函数名(); //赋值给其他变量;这里省略实参语法,下同。
B: $v1 = 函数名() * 3 + 6; //参与运算,然后再赋值;
C: echo 函数名(); //直接输出
D: echo 函数名() * 3 + 6; //参与运算,然后再输出
E: $v1 = 函数名2( 函数名() , 实参2,实参3, .... ); //当作实参使用
实际上,一个变量(数据)也只有这几种场合的使用情况。
其运行流程原理图如下:
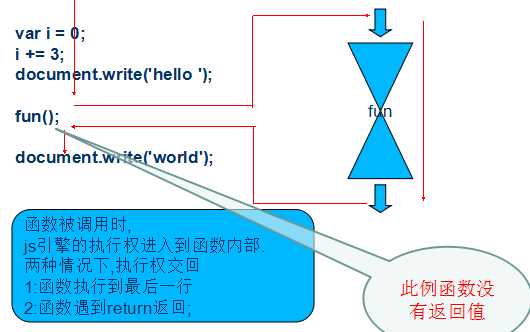
一个函数,
1,形参一定是一个变量名!
2,该变量名只能是在该函数中有效的变量名;
3,而且只在该函数调用并执行时有效,函数结束,通常这些变量也就“销毁”。
实参就是一个“实际数据”,
该数据可以是一个“直接数据”(比如5,”abc”),也可以是一个变量中存储的数据。
实参的作用是将其数据“赋值给”形参变量。
实参跟形参之间通常应该有个“一一对应”关系:
定义形式: function 函数名(形参1,形参2,...... ){ 。。。。}
调用形式: 函数名(实参1,实参2,..... )
定义一个函数的时候,在形式参数的位置,可以给形式参数设定“默认值”,此时就可以称为默认值参数。比如:

还要注意:
默认值不能是对象或资源类型;
默认值只能是常量表达式,或常量,不能是变量
即:如下语法是正确的:function f1($v1 = 3), function f1($v1 = __LINE__),
如下语法是错误的:function f1($v1 = 3+1), $m = 3; function f1($v1 = $m),
实际上,函数的参数传值问题,跟变量之间的传值问题,是一样的规则(模式):默认都是值传递。
如果实参本身就是“直接数据”,则不存在传值问题,而是简单的“赋值”。
传值问题只发生在实参是变量的情形:
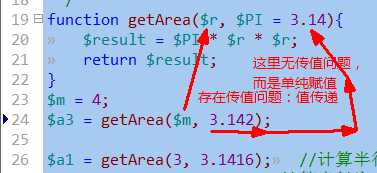
我们也可以让某个参数(形参)以引用传递的方式来传值:
引用传递的形参(实参),在函数内部改变其值,在函数外面的实参,也会相应修改:
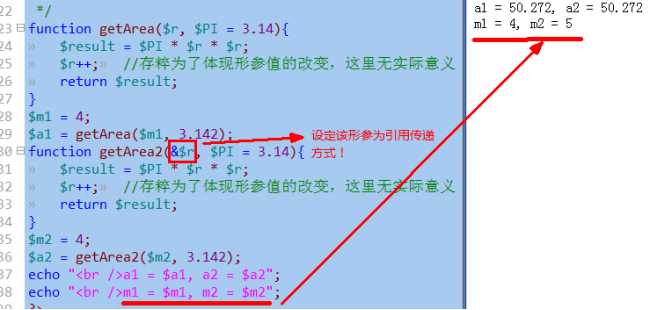
注意:如果某个形参设定为引用传递,此时,实参只能使用变量,否则出现语法错误:比如
1,函数的参数的数量可以是0个或多个——具体多少个,不是语法问题,而是应用问题。
2,通常,实际参数的数量应该跟形式参是的数量一致。
3,但是,在2的基础上,如果形式参是中有默认值,则实际参数的对应项可以省略。
即:实参的个数,至少应该不少于形参中的非默认值参数的个数。
但:
我们还有一种特殊的处理函数参数的用法:自由参数数量
定义时可以不给定形参,但调用时,却又可以给定任何个数的实参。
在系统中,var_dump()这个函数也有同样的使用效果:
var_dump($v1);
var_dump($v1, $v2, $v3);//也可以
这种应用的实现,是依赖与系统中的3个系统函数来达到的:
func_get_args();//获得一个函数所接收到的所有实参数据,并结果是一个数组
func_get_arg(n);//获得一个函数所接收到的第n歌实参数据(n从0开始)
func_num_args();//获得一个函数所接收到的所有实参数据的个数
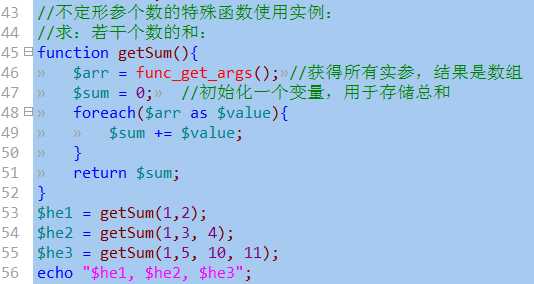
结果:
通常来说,一个函数中,使用return语句,并其后带一个数据(直接数据,变量数据,表达式结果数据)
则该函数就会返回该数据到“调用的位置”:
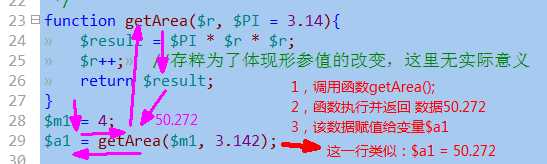
通常情况下,函数返回的数据都是以“值传递”的形式返回:函数中的变量的值“拷贝”一份,然后返回给接收的位置的相应代码(赋值,输出,计算)。
但:
我们也可以让函数中的变量数据的值,以“引用传递”的方式返回:
形式如下:
定义函数:
function &函数名(形参1,形参2,.....) //注意函数名前有个引用符号“&”
{
$result = 0; //初始化
。。。。。。。
return $result; //此时返回数据,只能是变量
}
调用函数:
$v1 = &函数名(实参1,实参2,....); //引用返回的函数,自然是指有返回值。

可变函数,就是函数名“可变”——其实跟可变变量一样的道理。
$str1 = “f1”; //只是一个字符串,内容为”f1”
$v1 = $str1(3, 4); //形式上看起来是一个变量后面加上括号,则其本质是该变量的“内容”(f1)后面加括号,即这里是调用函数f1(3, 4);

实际应用中,常常是需要根据“用户给定”的数据,来决定调用哪个函数,比如:
function jpg(){处理jpg图}
function png(){处理png图}
function gif(){处理gif图}
$fileName = get_fileName(){获取用户上传的图片名};
$houzhui = get_houzhui($fileName);
$houzhui();
匿名函数就是没有名字的函数,其有两种表现形式:
表现1:
$f1 = function(){。。。函数体;};
//这里的匿名函数定义形式上没有名字,但其实又将之赋值给了变量$f1
使用时,就跟“可变函数”一样了:$v1 = $f1();

表现形式2:
调用其他函数2(匿名函数,实参1,实参2, ...... );
说明:
1此形式的匿名函数只有定义的函数体(无函数名)
2此形式的匿名函数只能作为其他函数调用时的参数(其他函数通常有特定用处)
3此匿名函数会在调用其他函数的“过程中”被执行。
能够使用(匿名)函数当作实参的函数,并不多!
其中有一个常见的是:call_user_func_array();
其使用形式为:
call_user_func_array(匿名函数,数组);
含义:
将数组的每一项当作该匿名函数的若干个实参,传递到该匿名函数中,并执行该匿名函数,并可以从该匿名函数中返回数据。


通常说作用域,有2个:
局部作用域:只能在所定义的函数范围内使用。
全局作用域:在函数的“外部”范围使用。
——php中,局部和全局作用域是不重叠的
——js中,全局作用域是包括局部作用域的
但还有两个:
超全局:就是在函数的内部和外部都可以使用。
超全局变量只有系统内部预定义的那几个,我们不能再程序中创建超全局变量。
静态局部作用域:其实也是局部,但多一个特征:数据能够在函数退出后仍然保持不丢失。


1,在局部范围内,使用global关键字对全局变量进行一次“声明”,则就可以使用了:
语法:global $变量名;
举例:

说明:
1,实际上,函数中的global 语句,其实是创建了一个跟外部变量同名的局部变量,并通过“引用”的方式指向了外部变量的数据区
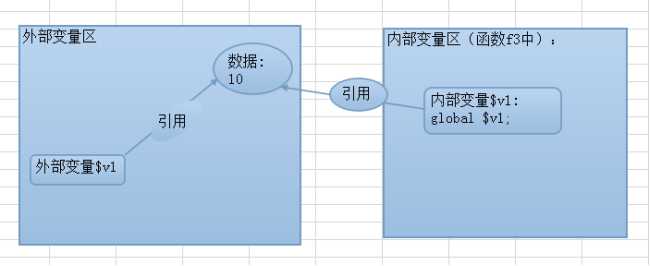
示例:

2,在函数中(局部范围),使用$GLOBALS超全局数组来引用(使用)全局变量:
$GLOBALS超全局数组的作用是用于存储所有全局变量的数据:变量名为下标,变量值为对应元素值。

但通过 $GLOBALS操作全局变量,是直接操作(而不是引用操作),即如果unset该对应元素,则全局变量对应变量也被unset:

3,实际上,我们还可以在函数内部直接使用$GLOBALS数组,添加元素的方式来创建全局变量,自然也就类似局部使用全局:
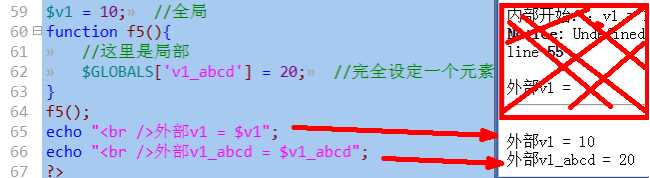
通过引用传递的方式向形参传递一个引用实参变量
$v1 = 10;
function f1( &$p1, $p2){ ...... } //$p1是函数的形参,也即就是函数的内部(局部)变量
$v2 = f1( $v1, 10); //此时我们认为$v1就可以使用函数中$p1的值。
使用函数的引用返回形式:见前面引用传递的方式返回数据
函数中使用global关键字来首次引用一个全局变量,则函数结束后在全局范围就可以使用该变量了

结果:
function_exists():判断某个函数是否被定义过,返回布尔值
if( function_exists(“ func1 “) == false ){
function func1(){。。。。。。};//定义函数
}
func_get_arg(n):获得一个函数的第n个实参值(n从0开始)
func_get_args():获得一个函数的所有实参,结果是一个数组
func_num_args():获得一个函数的所有实参的个数。
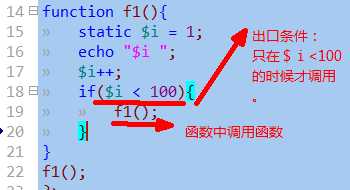
递归思想的一个基本形式是:在一个函数中,有至少一条语句,又会去调用该函数自身。
但是,从代码角度来说,如果单纯是函数内部调用函数本,则会出现“出不来”的现象。
则我们就必须再来解决下一个问题:
怎么终止(停止)这种调用——找到递归函数的出口。
案例分析:
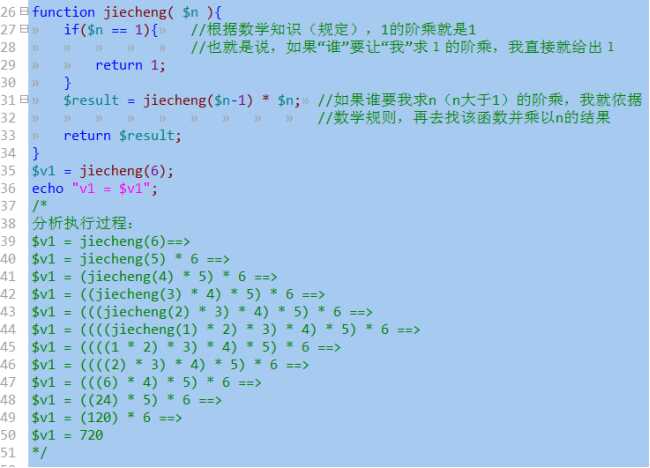
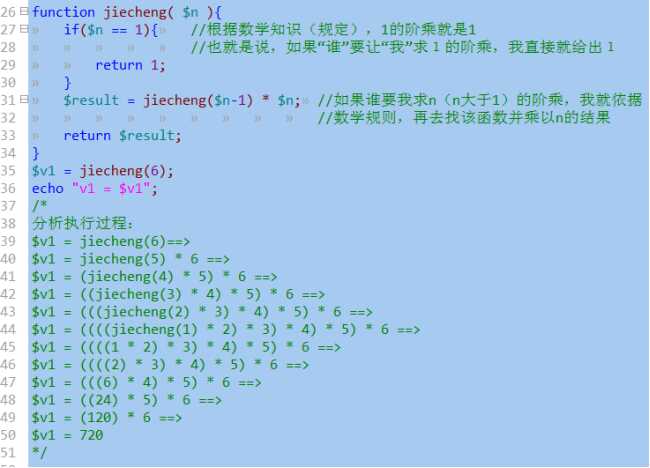
写一个递归函数,该函数可以计算一个正整数的阶乘:
数学基础:
A: 1的阶乘是1
B: 大于1的数的阶乘,是这个数减1的数的阶乘,乘以该数的结果。
比如:要求6的阶乘:
则定义一个函数jiecheng(){.....};该函数可以计算n的阶乘
递归思想的总结:
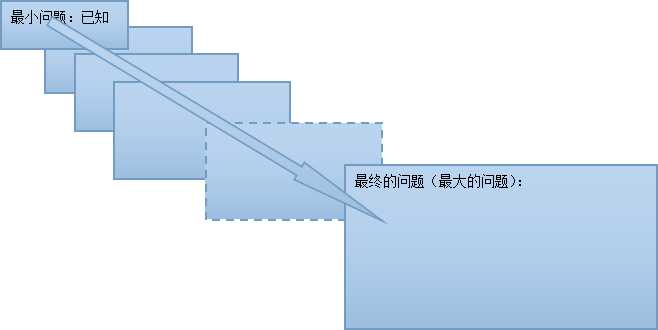
为了解决一个“大”问题,根据现实逻辑,该问题可以通过比它小一级的同类问题的答案而“轻松得到”。小一级的问题又可以通过更小一级的问题而轻松得到,依次类推——直到“最小问题”,通常就是一个已知数(答案)。
递归思想的图示
递推思想本身并不跟函数有直接关系(虽然常常写在函数中)。
其基本思路为:
为了解决一个“大”问题,根据现实逻辑,如果能够找到同类问题的一个“最小问题”的答案(通常是已知的),并且根据已知算法,又可以因此得到比最小问题“大一级”问题的答案。 而且,依次类推,又可以得到再大一级问题的答案,最终就可以得到“最大那个问题”(即要解决的问题)的答案。
可见,该思想的过程依赖与2个条件:
1,可知同类最小问题的答案;
2,大一级问题的答案可以通过小一级问题的答案经过简单运算规则而得到。
此思想的解体思路是:从小到大
对比:递归思想是:从大到小,在回归到大。
举例:求斐波那契数列的第n项的值。
斐波那契数列的规则是:某项的值是其前两项的值的和。
斐波那契数列的前几项为:1,1,2,3,5,8,13,21...(前两项是已知的)

递推算法的图示:
总结比较:
1,很多问题,用递归和递推都可以解决。
2,有些问题只能用递归。
3,如果两种方法都可以解决,推荐使用递推——效率高很多!
标签:weight 结束 数通 迭代思想 实现 局部变量 空间 简单的 创建
原文地址:https://www.cnblogs.com/ybygb-geng/p/9737868.html