标签:style blog class code c java
贝塞尔曲线(ezier curve)最迟是由法国物理学家与数学家paul de Casteljau发明的。它的广泛运用则要归功于法国工程师皮埃尔 贝塞尔
贝塞尔曲线期初被用在汽车车身的设计上。现在则多用于计算机图形系统中。例如Adobe Illustrator/Apple的Cocoa框架以及在Html5的canvas。
贝塞尔曲线分为两种:平方(quadratic)贝塞尔曲线及立方(cubic)贝塞尔曲线。平方贝塞尔曲线是一种二次曲线(second degree curve),意思就是说,它们是由三个点来定义的:两个锚点(anchor point)及一个控制点(control point)。而立方贝塞尔曲线则是一种三次曲线(third-degree curve),是由四个点来控制的:两个锚点及两个控制点。
canvas 支持平方及立方贝塞尔曲线。在接下来的数个小节中,我们将深入讲解如何使用Canvas来生成这些曲线。
二次方贝塞尔曲线:
二次方贝塞尔曲线是那种只向一个方向弯曲的简单曲线。下图程序展示的使用三条二次方贝塞尔曲线所拼合而成的一个复选框标记。

html代码:
1 <head> 2 <title>Bezier Curves: Quadratic</title> 3 4 <style> 5 body { 6 background: lightskyblue; 7 } 8 9 #text { 10 position: absolute; 11 left: 43px; 12 top: 15px; 13 display: inline; 14 color: navy; 15 } 16 17 #scaledCanvas { 18 position: absolute; 19 left: 75px; 20 top: 15px; 21 } 22 23 #text { 24 font: 16px Helvetica; 25 } 26 </style> 27 </head> 28 29 <body> 30 <canvas id=‘canvas‘ width=‘350‘ height=‘300‘> 31 Canvas not supported 32 </canvas> 33 34 <script src=‘example.js‘></script> 35 </body> 36 </html>
example.js代码:
1 var context = document.getElementById(‘canvas‘).getContext(‘2d‘); 2 3 context.fillStyle = ‘cornflowerblue‘; 4 context.strokeStyle = ‘yellow‘; 5 6 context.shadowColor = ‘rgba(50, 50, 50, 1.0)‘; 7 context.shadowOffsetX = 2; 8 context.shadowOffsetY = 2; 9 context.shadowBlur = 4; 10 11 context.lineWidth = 20; 12 context.lineCap = ‘round‘; 13 14 context.beginPath(); 15 context.moveTo(120.5, 130); 16 context.quadraticCurveTo(150.8, 130, 160.6, 150.5); 17 context.quadraticCurveTo(190, 250.0, 210.5, 160.5); 18 context.quadraticCurveTo(240, 100.5, 290, 70.5); 19 context.stroke();
你可以通过quadraticCurveTo()方法来绘制二次方贝塞尔曲线,改函数接受四个参数,分别表示两个点的X与Y坐标。第一个是曲线的控制点,用于决定该曲线的形状。第二个点是锚点。quadraticCurveTo()方法所绘制的贝塞尔曲线,会将锚点与当前路径中的最后一个点连接起来。
二次方贝塞尔曲线的用途很多。举例来说,下图的应用程序使用二次方贝塞尔曲线来绘制箭头形状的三个尖端。该应用程序还将每条曲线的控制点与锚点也标注了出来。
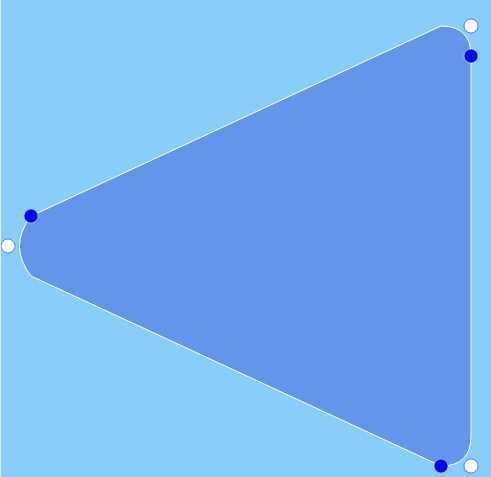
使用贝塞尔曲线累绘制圆角:白色的点表示控制点,深色的点表示锚点
该图所示应用程序的代码如下清单:
html代码:
1 <head> 2 <title>Quadratic Curves</title> 3 4 <style> 5 body { 6 background: #eeeeee; 7 } 8 9 #canvas { 10 position: absolute; 11 left: 0px; 12 margin-left: 20px; 13 margin-right: 20px; 14 background: lightskyblue; 15 border: thin solid rbga(0,0,0,1.0); 16 -webkit-box-shadow: rgba(0,0,0,0.5) 4px 4px 6px; 17 -moz-box-shadow: rgba(0,0,0,0.5) 4px 4px 6px; 18 box-shadow: rgba(0,0,0,0.5) 4px 4px 6px; 19 } 20 21 input { 22 margin-left: 15px; 23 } 24 25 </style> 26 </head> 27 28 <body> 29 <canvas id=‘canvas‘ width=‘500‘ height=‘500‘> 30 canvas not supported 31 </canvas> 32 33 <script src=‘example.js‘></script> 34 </body> 35 </html>
example.js代码:
1 var canvas = document.getElementById(‘canvas‘), 2 context = canvas.getContext(‘2d‘), 3 ARROW_MARGIN = 30, 4 POINT_RADIUS = 7, 5 points = [ 6 { x: canvas.width - ARROW_MARGIN, 7 y: canvas.height - ARROW_MARGIN }, 8 9 { x: canvas.width - ARROW_MARGIN*2, 10 y: canvas.height - ARROW_MARGIN }, 11 12 { x: POINT_RADIUS, 13 y: canvas.height/2 }, 14 15 { x: ARROW_MARGIN, 16 y: canvas.height/2 - ARROW_MARGIN }, 17 18 { x: canvas.width - ARROW_MARGIN, 19 y: ARROW_MARGIN }, 20 21 { x: canvas.width - ARROW_MARGIN, 22 y: ARROW_MARGIN*2 }, 23 ]; 24 25 // Functions.......................................................... 26 27 function drawPoint(x, y, strokeStyle, fillStyle) { 28 context.beginPath(); 29 context.fillStyle = fillStyle; 30 context.strokeStyle = strokeStyle; 31 context.lineWidth = 0.5; 32 context.arc(x, y, POINT_RADIUS, 0, Math.PI*2, false); 33 context.fill(); 34 context.stroke(); 35 } 36 37 function drawBezierPoints() { 38 var i, 39 strokeStyle, 40 fillStyle; 41 42 for (i=0; i < points.length; ++i) { 43 fillStyle = i % 2 === 0 ? ‘white‘ : ‘blue‘, 44 strokeStyle = i % 2 === 0 ? ‘blue‘ : ‘white‘; 45 46 drawPoint(points[i].x, points[i].y, 47 strokeStyle, fillStyle); 48 } 49 } 50 51 function drawArrow() { 52 context.strokeStyle = ‘white‘; 53 context.fillStyle = ‘cornflowerblue‘; 54 55 context.moveTo(canvas.width - ARROW_MARGIN, 56 ARROW_MARGIN*2); 57 58 context.lineTo(canvas.width - ARROW_MARGIN, 59 canvas.height - ARROW_MARGIN*2); 60 61 context.quadraticCurveTo(points[0].x, points[0].y, 62 points[1].x, points[1].y); 63 64 context.lineTo(ARROW_MARGIN, 65 canvas.height/2 + ARROW_MARGIN); 66 67 context.quadraticCurveTo(points[2].x, points[2].y, 68 points[3].x, points[3].y); 69 70 context.lineTo(canvas.width - ARROW_MARGIN*2, 71 ARROW_MARGIN); 72 73 context.quadraticCurveTo(points[4].x, points[4].y, 74 points[5].x, points[5].y); 75 context.fill(); 76 context.stroke(); 77 } 78 79 // Initialization..................................................... 80 81 context.clearRect(0,0,canvas.width,canvas.height); 82 drawArrow(); 83 drawBezierPoints();
html5 canvas绘图-贝塞尔曲线,布布扣,bubuko.com
标签:style blog class code c java
原文地址:http://www.cnblogs.com/zxmeigood/p/3725704.html