标签：分析   文献   出现   浮点数   部分   编码方式   art   研究   tps   

遗传算法入门C1

觉得有用的话,欢迎一起讨论相互学习~Follow Me

参考文献

遗传算法历史

• 遗传算法(GA)是从生物进化的角度考虑提出来的方法，19世纪达尔文在大量观察基础上总结了大自然进化规律，即优胜劣汰：后来孟德尔通过豌豆实验发现了遗传规律、分离规律和自由组合规律。遗传是指父代的基因将会遗传到子代中去，父代和子代具有相似性，同时，父代与子代也会有不同点，否则，从进化角度考虑，父代和子代无差别，物种没有出现进化。当子代中出现不适应生存的个体时，将会逐渐被环境淘汰，具有环境生存优势的个体将生存下来，这样遗传通过基因传递，并和环境相互作用，让基因朝着有利于生存的方向进化，优良的基因库就得以保存。
• 在19世纪60年代，科学家Fraser在其论文中首先提到了选择和突变操作。密西
  根大学教授J．Holland在20世纪70年代研究自然和人工自适应系统时，首先提出了遗传算法基本形式。在80年代Goldberg根据前人研究成果，将遗传算法主要过程分为 选择、遗传和变异三部分 。由于遗传算法适应能力较强，同时具备较强的全局搜索能力，使遗传算法在各个领域都得到了广泛的应用，同时也促使遗传算法在理论上得到了很大的发展

• 运用遗传算法求解实际问题时， 我们需要将目标问题同遗传算法建立联系， 即通过遗传编码建立关联。 每一个编码可以称为个体或者染色体，多个解的个体构成了种群。 遗传算法通过模拟生物进化对种群中个体进行 选择、交叉、变异操作 ，能将优秀的基因保留下来，传递给后代，使种群向最优方向进化。

  遗传编码

• 运用遗传算法寻求最优解时，在确定目标函数后，需要把函数变量转化成染色体表现形式，编码的过程必须满足以下条件：
  1. 必须保证解的空间中的所有解都在编码空间内
  2. 每一个解都能通过交叉和变异操作转化成解的空间中其他任意解
  3. 每一个染色体都是对应解的空间内的一个特定解

• 遗传编码方式很重要，同一问题不同的编码方式可能使遗传算法的出来的结果出现较大的差异，好的编码方式能提高求解效率，因此，需要根据求解问题的特点决定编码方式。根据前人总结，编码方式一般有二进制编码、浮点数编码和格雷码编码等编码形式。

  适应度函数

• 遗传算法为了保证种群向着对环境适应能力较强的方向进化，就需要一个 评价标准 保证某一代中较优秀的个体能 有较大的概率将基因遗传给下一代 ，因此，遗传算法中就引入了 适应度函数 的概念。 个体中适应度值较大，其个体就有较大的概率遗传给下一代 反之，适应度值小的，其个体淘汰的概率就比较高，模拟进化过程中的优胜劣汰。

遗传操作

选择

选择操作的目的是为了将 当代 种群中 适应度值较高 的个体保存下来，将 适应度值低的个体淘汰 ，选择操作的过程中 本身不会产生任何新的个体 。但是选择操作由于是一个 随机选择过程 ，只是表示适应度值较高的个体将 有较高的概率 将自身基因遗传给下一代，并不表示适应度值较低的个体一定会淘汰， 但是，总体的趋势会是基因库中的基因越来越好，适应度值越来越高。选择操作的方法目前主要有 轮盘赌选择、最优保留法、期望值法 等等。

轮盘赌选择法

• 轮盘赌选择法又称为比例选择法，其选择方式是随机的，不过适应度值较高的被选择的概率大。设定种群规模为N，其中个体i的适应度值为\(f_i\)，在选择操作中其被选中的概率为：\[P_i=\frac{f_i}{\sum^{N}_{i=1}f_{i}}\]
  由于轮盘赌选择法是随机选择的，因此，有可能将适应度值较大的个体淘汰，导致最终结果可能不能寻找到最优解，通常，可以将 最优保留法和轮盘赌选择法结合选择 ，先通过 最优保留法 将适应度值最高的个体保留，之后再进行 轮盘赌选择法进行选择

  交叉

• 交叉操作在遗传算法中占据比较重要的作用，遗传算法中 产生新个体的主要就是通过交叉操作完成的 交叉操作的具体过程是 父代随机选取两个个体，按照某种规则对染色体上的基因相互交换，形成新的个体 ，这样做的目的是 为了将优秀的基因段通过交叉的方式有效进行整合，使下一代个体的适应度值比上一代更高 。常见的交叉规则有 单点交叉、多点交叉和均匀交叉 三种方式。
  • 单点交叉 的方式是在染色体上随机选定一个基因点作为交叉位置，父代中两染色体在此处的基因信息互换，这样就形成了两个子代个体。如下图所示，对其基因采用二进制编码，若随机交叉点为第三基因位。
    
  • 多点交叉 是指染色体中有 两个或两个以上的基因位点交叉 ，图中染色体同样采用二进制编码，假定多点交叉为随机取两个基因位点交叉。若交叉点发生在第二、三基因位。
    
  • 均匀交叉 其交叉通过两父代染色体之间设置一个屏蔽码来实现的， 屏蔽码的长度需要与染色体上的基因为长度一致 如下图所示，图中在父代染色体中出现了一串屏蔽码，使用规则为： 凡是屏蔽码中码为1时，父代染色体中与之对应的基因位发生交叉互换；凡是屏蔽码中码为0，则与之对应的父代染色体基因位不进行交叉操作
    

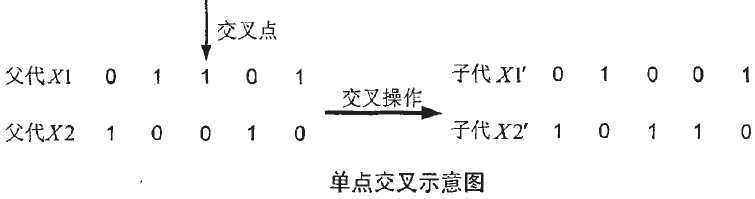
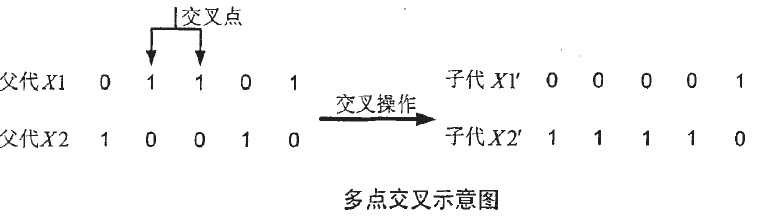
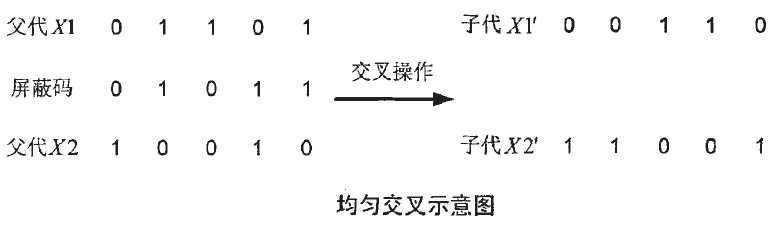
• 遗传交叉操作方式的选取对遗传算法效率影响较大，具体采用何种交叉方式取决于实际问题情况，总之无论采取哪种交叉方式，都需要 保证种群基因多样性，不然容易使遗传算法陷入早熟。但是，交叉点太多，又极可能导致遗传算法无法收敛

  变异

• 生物进化过程中，在外在环境发生较大变化时，某些物种大部分个体由于环境变化而消亡，但是有极少数个体能够生存下来，其原因是因为环境发生大的变化时，其个体内的基因发生了突变，基因突变导致出现了新的基因出现，而此基因能适应改变后的环境。显然，变异操作也在遗传算法中对保持种群多样性、防止早熟、丰富基因库有着重大意义。
• 变异操作的概念是指种群中任意个体以一定的概率使其染色体中一个或几个基因位发生突变。这种操作很有可能出现原有种群通过交叉获取不到的基因表现形式，在丰富种群基因库同时也能防止遗传算法过早的收敛。下图为对基因位的变异操作过程，取变异基因位为第一位
  

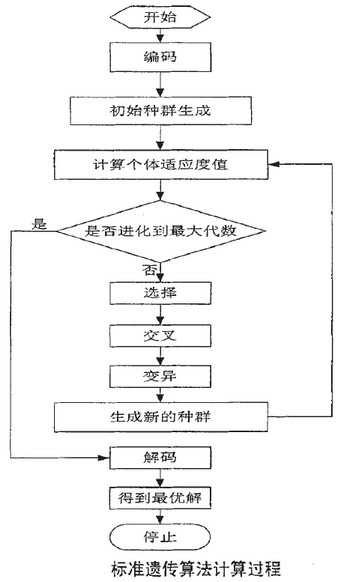
• 遗传编码、选择、交叉和变异组成了遗传算法的基本框架 ，即遗传算法的标准组成部分，其操作过程都是采用随机操作，有一定能力 跳出局部最优 ，具有较好的 全局搜索能力 。通过对遗传算法的编码形式的分析，可以得出遗传算法在面对 非线性、不连续、离散型 问题时，具有较强的处理能力，在解决实际问题中具有较强的适应能力。下图是一个标准遗传算法的程序流程图，严格按照选择、交叉和变异来进行，在达到终止条件时，遗传进化停止，输入所求得最优解。
  

遗传算法入门C1

标签：分析   文献   出现   浮点数   部分   编码方式   art   研究   tps   

原文地址：https://www.cnblogs.com/cloud-ken/p/9740829.html