标签:指令 包括 数学 color 现在 inf uri 一个 允许
为了算法复杂性分析具有普适性,即一个算法的性能与具体的计算机无关,我们需要选定一种可用于描述计算的计算机模型。
图灵机
图灵机本质上是一个具有存储载体(通常用一个有无限多个方格线性带表示)的、按照具体指令可完成向左或右移动、放置标记、抹去标记以及在计算终止时停机等四种基本操作的、用于描述算法的语言。
图灵机在原理上,与我们用于和计算机交流的更为复杂的各种程序语言同样有力。
首先选择确定性单带图灵机(deterministic one-tape Turing machine),简称确定图灵机,记为DTM。一个DTM由一个有限状态控制器、一个读写头和一条双向的具有无限多个格的线性带所组成。
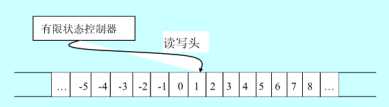
单带确定性图灵机示意图
一个DTM程序应详细规定以下信息:

非确定性单带图灵机(non-deterministic one-tape Turing machine),简记为NDTM,是一种假想的机器。通常有两种方式描述它:多值模型和猜想模块模型。
多值模型认为它和确定性图灵机的共同之处是也包括:

不同之处在于
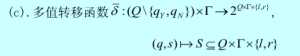
确定性图灵机在任一状态下只能做一种运算,而非确定性图灵机可以被想象为在同一时刻能够独立、并行地完成多种运算(表现在转移函数的多值性),这显然不现实。
通过允许作不受限制的并行运算可以对不确定性算法做出明确的解释。每当要作某种选择时,算法就好像给自己复制了若干副本,每种可能的选择有一个副本,于是,许多副本同时被执行。第一个获得成功的副本将引起对其它副本计算的结束。如果一个副本获得不成功的完成则只改副本终止。
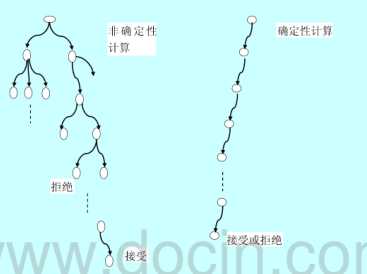
非确定性算法与确定性算法比较
“猜想模块模型”是另一种更形象、直观的解释方法。可将NDTM描述成:除多了一个猜想模块外,NDTM与DTM有着完全相同的结构,而这个猜想模块带有自己的仅可对带进行写操作的猜想头,它提供写下猜想的方法,仅此而已。
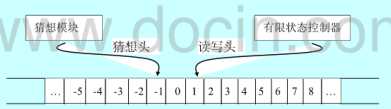
NDTM猜想模块模型示意图



因为任何现有的计算模型都可以通过加上一个类似于NDTM中的带有只写头的猜想模块来扩充,然后相对于所得的模型重新描述上述的正式定义,而且所有如此得到的计算模型在多项式时间内可相互转换的意义下将是等价的。因此,也没有必要特别提及NDTM模型,我们将简单地说“多项式时间不确定性算法”,并将NP类语言与所有可用多项式时间不确定性算法求解的判断问题等同看待。
证明NP=P?
1.证明NP类中的某些问题是难解的,从而得到P≠NP。但是这同原问题的难度几乎相当,也许只有建立一套全新的数学论证方法才有希望解决。
2.考虑NP类中问题之间的关系,从中找到一些具有特定性质的、与P中问题有显著不同的问题。沿此路线人们已经证明了在NP类中存在一个称为NP-完全的子类,并由此发展出一套著名的NP-完全理论。而证明一个问题是NP-完全的通常被认为一个告诉我们应该放弃寻找、设计求解该问题的有效算法(多项式时间算法)的强有力证明。
标签:指令 包括 数学 color 现在 inf uri 一个 允许
原文地址:https://www.cnblogs.com/zhangzefei/p/9742918.html