标签:计算 情况 规则 环境 表达式 需要 统计 ret 说明
复杂度分析就是分析执行一个给定算法需要消耗的计算资源数量(例如计算时间,存储器使用等)的过程。
把代码运行一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小。
该方法的缺点在于:
拿同样一段代码,在 Intel Core i9 处理器上运行的速度肯定要比 Intel Core i3 快得多。同一段代码,在不同机器上运行,也可能会有截然相反的结果。
以排序算法举个例子。对同一个排序算法,待排序数据的有序度不一样,排序的执行时间就会有很大的差别。极端情况下,如果数据已经是有序的,那排序算法不需要做任何操作,执行时间就会非常短。除此之外,如果测试数据规模太小,测试结果可能无法真实地反应算法的性能。比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快!
不需要用具体的测试数据来测试,就可以粗略地估计算法的执行效率。
下面有一段代码,来估算一下这段代码的执行时间:
1 int cal(int n) { 2 int sum = 0; 3 int i = 0; 4 int j = 0; 5 for (; i < n; ++i) { 6 j = 1; 7 for (; j < n; ++j) { 8 sum = sum + i * j; 9 } 10 } 11 }
假设每行代码执行的时间都一样,为 unit_time,在这个假设的基础之上,我们可以看出:第 2、3、4 行代码分别需要 1 个 unit_time 的执行时间,第 5、6 行都运行了 n 遍,所以需要 2n*unit_time 的执行时间,第 7、8 行代码循环执行了 n^2遍,所以需要 2n^2 * unit_time 的执行时间。所以,整段代码总的执行时间 T(n) = (2n^2+2n+3)*unit_time。
通过这段代码执行时间的推导过程,我们可以知道,所有代码的执行时间 T(n) 与每行代码的执行次数 n 成正比。用大 O 复杂度表示法可以这样表示:T(n) = O(f(n))
其中,T(n) 表示代码执行的时间;n 表示数据规模的大小;f(n) 表示每行代码执行的次数总和。公式中的 O,表示代码的执行时间 T(n) 与 f(n) 表达式成正比。
分析一段代码的时间复杂度三个比较实用的方法:
在进行时间复杂度分析的时候,我们通常会忽略掉公式中的常量、低阶、系数,只记录一个最大阶的量级。所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。
假设有这样三段代码,每段代码是一个for循环,第一段代码循环了 100 次,第二段代码循环了 n 次,第三段代码循环了 n^2 次。
那么,第一段代码的时间复杂度是一个常量,跟 n 的规模无关。第二段代码和第三段代码的时间复杂度分别为 O(n) 和 O(n^2)。
因为总的时间复杂度就等于量级最大的那段代码的时间复杂度,所以,整段代码的时间复杂度为 O(n^2)。那我们将这个规律抽象成公式就是:
如果 T1(n)=O(f(n)),T2(n)=O(g(n));
那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))
复杂度分析中还有一个乘法法则。
如果 T1(n)=O(f(n)),T2(n)=O(g(n));
那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))。
常见的嵌套循环,其时间复杂度就可以用乘法法则进行计算 。
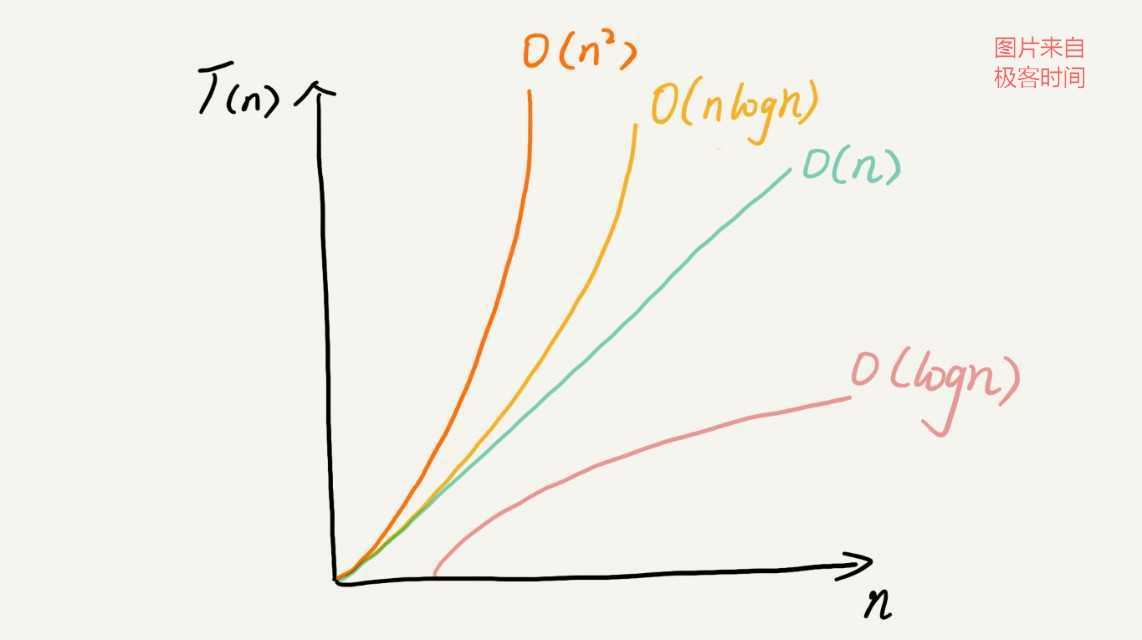
常见的复杂度量级并不多,大概就是下图中包含的:

复杂度量级可以分为多项式量级和非多项式量级。其中,非多项式量级只有两个:O(2^n) 和 O(n!)。
对于多项式量级,随着数据规模的增长,算法的执行时间和空间占用统一呈多项式规律增长;而对于非多项式量级,随着数据规模的增长,其时间复杂度会急剧增长,执行时间无限增加;
这里主要来看几种常见的多项式时间复杂度:
O(1) 只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度我们都记作 O(1)。或者说,一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
最难分析的是对数阶时间复杂度,这里通过一个例子来说明一下。
1 i = 1; 2 while (i <= n) { 3 i = i * 2; 4 }
我们已经知道,只要关注循环执行次数最多的那一段代码就可以了,这里循环执行次数最多的是第 3 行代码,所以,我们只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。 从代码中可以看出,变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结束。观察变量 i 的增长规律,我们可以发现,它的取值是一个等比数列。如果我们把它一个一个列出来,就应该是这个样子的:

理解了 O(logn),那 O(nlogn) 就很容易理解了。前面我们讲了时间复杂度分析的乘法法则,如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,那么时间复杂度就是 O(nlogn) 了。(常见的归并排序、快速排序的时间复杂度都是 O(nlogn))
来看这样一段代码:
1 int cal(int m, int n) { 2 int sum_1 = 0; 3 int i = 0; 4 for (; i < m; ++i) { 5 sum_1 = sum_1 + i; 6 } 7 8 int sum_2 = 0; 9 int j = 0; 10 for (; j < n; ++j) { 11 sum_2 = sum_2 + j; 12 } 13 14 return sum_1 + sum_2; 15 }
从代码中可以看出,m 和 n 是表示两个未知的数据规模,其大小关系也无法确定,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是 O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))。
相比起时间复杂度分析,空间复杂度分析方法学起来就非常简单了。
这里也举一个例子进行说明:
1 void print(int n) {
2 int i = 0;
3 int[] a = new int[n];
4 for (i; i <n; ++i) {
5 a[i] = i * i;
6 }
7 }
这里第 3 行申请了一个大小为 n 的 int 类型数组,除此之外,其余代码所占空间都是可以忽略的,所以整段代码的空间复杂度就是 O(n)。
我们常见的空间复杂度就是 O(1)、O(n)、O(n^2 ),像 O(logn)、O(nlogn) 这样的对数阶空间复杂度平时都用不到,相比起来,空间复杂度分析比时间复杂度分析要简单很多。
总结一下:复杂度包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系,越高阶复杂度的算法,执行效率越低。常见的复杂度从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n^2 )。
标签:计算 情况 规则 环境 表达式 需要 统计 ret 说明
原文地址:https://www.cnblogs.com/hardyyao/p/9744418.html