c语言数字图像处理（五）：空间滤波

时间：2018-10-05 15:04:03 阅读：538 评论：0 收藏：0 [点我收藏+]

标签：for 图像 sha value ble 效果 text lock sum

空间滤波原理

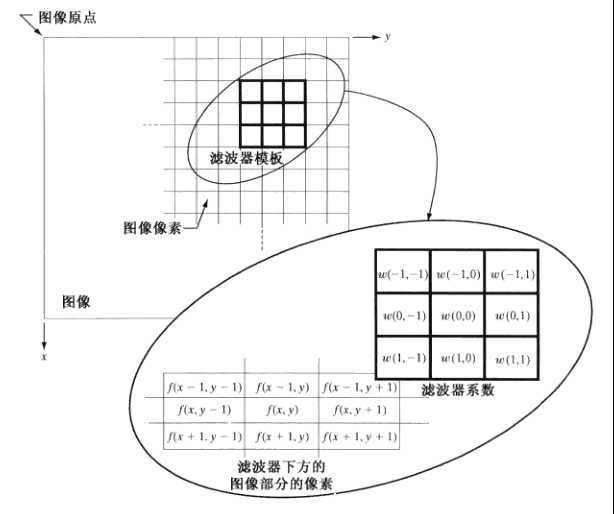
技术分享图片

使用大小为m*n的滤波器对大小为M*N的图像进行线性空间滤波，将滤波器模板乘以图像中对应灰度值，相加得模板中心灰度值

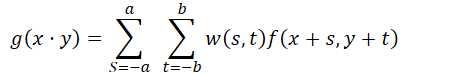
技术分享图片

a = (m-1)/2, b = (n-1)/2

若f(x+s, y+t)不在原图内，补0

平滑线性滤波器

滤波过程

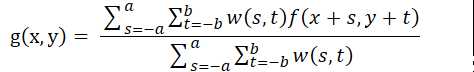
技术分享图片

分母为滤波器模板和

代码实现

 1 int is_in_array(short x, short y, short height, short width)
 2 {
 3     if (x >= 0 && x < width && y >= 0 && y < height)
 4         return 1;
 5     else
 6         return 0;
 7 }
 8 
 9 /*
10  * element
11  * v0  v1  v2
12  * v3  v4  v5
13  * v6  v7  v8
14  *
15  */
16 void filtering(short** in_array, short** out_array, long height, long width)
17 {
18     short value[9];
19 
20     /* linear filtering */
21      short sum;
22      for (int i = 0; i < ARRAY_SIZE; i++)
23          for (int j = 0; j < ARRAY_SIZE; j++)
24              sum += average[i][j];
25 
26     for (int i = 0; i < height; i++){
27         for (int j = 0; j < width; j++){
28             value[0] = is_in_array(j-1, i-1, height, width) ? in_array[i-1][j-1] : 0;
29             value[1] = is_in_array(j, i-1, height, width) ? in_array[i-1][j] : 0;
30             value[2] = is_in_array(j+1, i-1, height, width) ? in_array[i-1][j+1] : 0;
31             value[3] = is_in_array(j-1, i, height, width) ? in_array[i][j-1] : 0;
32             value[4] = in_array[i][j];
33             value[5] = is_in_array(j+1, i, height, width) ? in_array[i][j+1] : 0;
34             value[6] = is_in_array(j-1, i+1, height, width) ? in_array[i+1][j-1] : 0;
35             value[7] = is_in_array(j, i+1, height, width) ? in_array[i+1][j] : 0;
36             value[8] = is_in_array(j+1, i+1, height, width) ? in_array[i+1][j+1] : 0;
37 
38             /* linear filtering */
39              out_array[i][j] = (value[0] * average[0][0] + value[1] * average[0][1] + value[2] * average[0][2] +
40                                 value[3] * average[1][0] + value[4] * average[1][1] + value[5] * average[1][2] +
41                                 value[6] * average[2][0] + value[7] * average[2][1] + value[8] * average[2][2]) / sum;
42 
43         }
44     }
45 }

原图

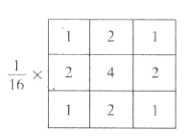
技术分享图片

模板

技术分享图片

结果

技术分享图片

可以看出线性滤波器会较大程度地影响原图，降低对比度，对与图片右上角的噪声没有明显的去除效果

统计排序（非线性）滤波器

中值滤波器

中值滤波器对处理脉冲噪声非常有效，这种噪声被称为椒盐噪声

实现方法：取该像素某邻域中值（本次测试取3*3)

代码实现

 1 short mid_val(short* a, short num)
 2 {
 3     short temp;
 4 
 5     for (int i = 0; i < num; i++)
 6     {
 7         temp = a[i];
 8         int j = i;
 9         for (; j > 0 && a[j - 1] > temp; j--)
10             a[j] = a[j - 1];
11         a[j] = temp;
12     }
13 
14     return a[num/2];
15 }
16 int is_in_array(short x, short y, short height, short width)
17 {
18     if (x >= 0 && x < width && y >= 0 && y < height)
19         return 1;
20     else
21         return 0;
22 }
23 
24 /*
25  * element
26  * v0  v1  v2
27  * v3  v4  v5
28  * v6  v7  v8
29  *
30  */
31 void filtering(short** in_array, short** out_array, long height, long width)
32 {
33     short value[9];
34 
35     for (int i = 0; i < height; i++){
36         for (int j = 0; j < width; j++){
37             value[0] = is_in_array(j-1, i-1, height, width) ? in_array[i-1][j-1] : 0;
38             value[1] = is_in_array(j, i-1, height, width) ? in_array[i-1][j] : 0;
39             value[2] = is_in_array(j+1, i-1, height, width) ? in_array[i-1][j+1] : 0;
40             value[3] = is_in_array(j-1, i, height, width) ? in_array[i][j-1] : 0;
41             value[4] = in_array[i][j];
42             value[5] = is_in_array(j+1, i, height, width) ? in_array[i][j+1] : 0;
43             value[6] = is_in_array(j-1, i+1, height, width) ? in_array[i+1][j-1] : 0;
44             value[7] = is_in_array(j, i+1, height, width) ? in_array[i+1][j] : 0;
45             value[8] = is_in_array(j+1, i+1, height, width) ? in_array[i+1][j+1] : 0;
46 
47             /* median filtering */
48             out_array[i][j] = mid_val(value, 9);
49 
50         }
51     }
52 }

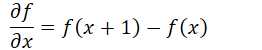
技术分享图片

锐化空间滤波器

一阶微分

技术分享图片

二阶微分

技术分享图片

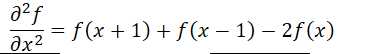
二阶微分在增强细节方面比一阶微分好很多，适合锐化图像

使用二阶微分进行图像锐化-拉普拉斯算子

技术分享图片

代码实现

 1 int is_in_array(short x, short y, short height, short width)
 2 {
 3     if (x >= 0 && x < width && y >= 0 && y < height)
 4         return 1;
 5     else
 6         return 0;
 7 }
 8 
 9 /*
10  * element
11  * v0  v1  v2
12  * v3  v4  v5
13  * v6  v7  v8
14  *
15  */
16 void filtering(short** in_array, short** out_array, long height, long width)
17 {
18     short value[9];
19 
20     for (int i = 0; i < height; i++){
21         for (int j = 0; j < width; j++){
22             value[0] = is_in_array(j-1, i-1, height, width) ? in_array[i-1][j-1] : 0;
23             value[1] = is_in_array(j, i-1, height, width) ? in_array[i-1][j] : 0;
24             value[2] = is_in_array(j+1, i-1, height, width) ? in_array[i-1][j+1] : 0;
25             value[3] = is_in_array(j-1, i, height, width) ? in_array[i][j-1] : 0;
26             value[4] = in_array[i][j];
27             value[5] = is_in_array(j+1, i, height, width) ? in_array[i][j+1] : 0;
28             value[6] = is_in_array(j-1, i+1, height, width) ? in_array[i+1][j-1] : 0;
29             value[7] = is_in_array(j, i+1, height, width) ? in_array[i+1][j] : 0;
30             value[8] = is_in_array(j+1, i+1, height, width) ? in_array[i+1][j+1] : 0;
31 
32             /* sharpening filtering */
33             out_array[i][j] = value[0] * sharpen[0][0] + value[1] * sharpen[0][1] + value[2] * sharpen[0][2] +
34                               value[3] * sharpen[1][0] + value[4] * sharpen[1][1] + value[5] * sharpen[1][2] +
35                               value[6] * sharpen[2][0] + value[7] * sharpen[2][1] + value[8] * sharpen[2][2];
36             out_array[i][j] += in_array[i][j];
37
38         }
39     }
40 }

原图

技术分享图片

锐化

技术分享图片

使用一阶微分对（非线性）图像锐化-梯度

实现边缘增强

技术分享图片

算法实现

 1 int is_in_array(short x, short y, short height, short width)
 2 {
 3     if (x >= 0 && x < width && y >= 0 && y < height)
 4         return 1;
 5     else
 6         return 0;
 7 }
 8 
 9 /*
10  * element
11  * v0  v1  v2
12  * v3  v4  v5
13  * v6  v7  v8
14  *
15  */
16 void filtering(short** in_array, short** out_array, long height, long width)
17 {
18     short value[9];
19 
20     for (int i = 0; i < height; i++){
21         for (int j = 0; j < width; j++){
22             value[0] = is_in_array(j-1, i-1, height, width) ? in_array[i-1][j-1] : 0;
23             value[1] = is_in_array(j, i-1, height, width) ? in_array[i-1][j] : 0;
24             value[2] = is_in_array(j+1, i-1, height, width) ? in_array[i-1][j+1] : 0;
25             value[3] = is_in_array(j-1, i, height, width) ? in_array[i][j-1] : 0;
26             value[4] = in_array[i][j];
27             value[5] = is_in_array(j+1, i, height, width) ? in_array[i][j+1] : 0;
28             value[6] = is_in_array(j-1, i+1, height, width) ? in_array[i+1][j-1] : 0;
29             value[7] = is_in_array(j, i+1, height, width) ? in_array[i+1][j] : 0;
30             value[8] = is_in_array(j+1, i+1, height, width) ? in_array[i+1][j+1] : 0;
31 
32             /* sharpening using grad */
33             out_array[i][j] = (short)abs(value[0] * soble1[0][0] + value[1] * soble1[0][1] + value[2] * soble1[0][2] +
34                                          value[3] * soble1[1][0] + value[4] * soble1[1][1] + value[5] * soble1[1][2] +
35                                          value[6] * soble1[2][0] + value[7] * soble1[2][1] + value[8] * soble1[2][2]) + 
36                               (short)abs(value[0] * soble2[0][0] + value[1] * soble2[0][1] + value[2] * soble2[0][2] +
37                                          value[3] * soble2[1][0] + value[4] * soble2[1][1] + value[5] * soble2[1][2] +
38                                          value[6] * soble2[2][0] + value[7] * soble2[2][1] + value[8] * soble2[2][2]);
39         }
40     }
41 }