树状数组维护区间最值

标签：lowbit   span   最大   前缀   维护   最大值   参考   直接   href   

参考:(LbyG: 树状数组求区间最大值)https://blog.csdn.net/u010598215/article/details/48206959
支持两种操作:

1. 修改一个位置的数;
2. 求区间最值;

当然不能像普通的树状数组维护区间和一样做

单点修改

先来看一份代码:

while(x <= n) {
    t[x] = max(t[x], a[u])
    x += lowbit(x);
}

这个代码当然是不对的, 为什么呢?
将一个可能是区间最大值的数换成一个更小的数, 但是最大值并没有变小.

因为树状数组每个位置所维护的区间是\((x - lowbit_x, x)\)
因此需要将包含这个位置的区间全部置0然后更新一遍.

当然这个过程画画图才能明白, 毕竟树状数组就是一个比较抽象的东西.

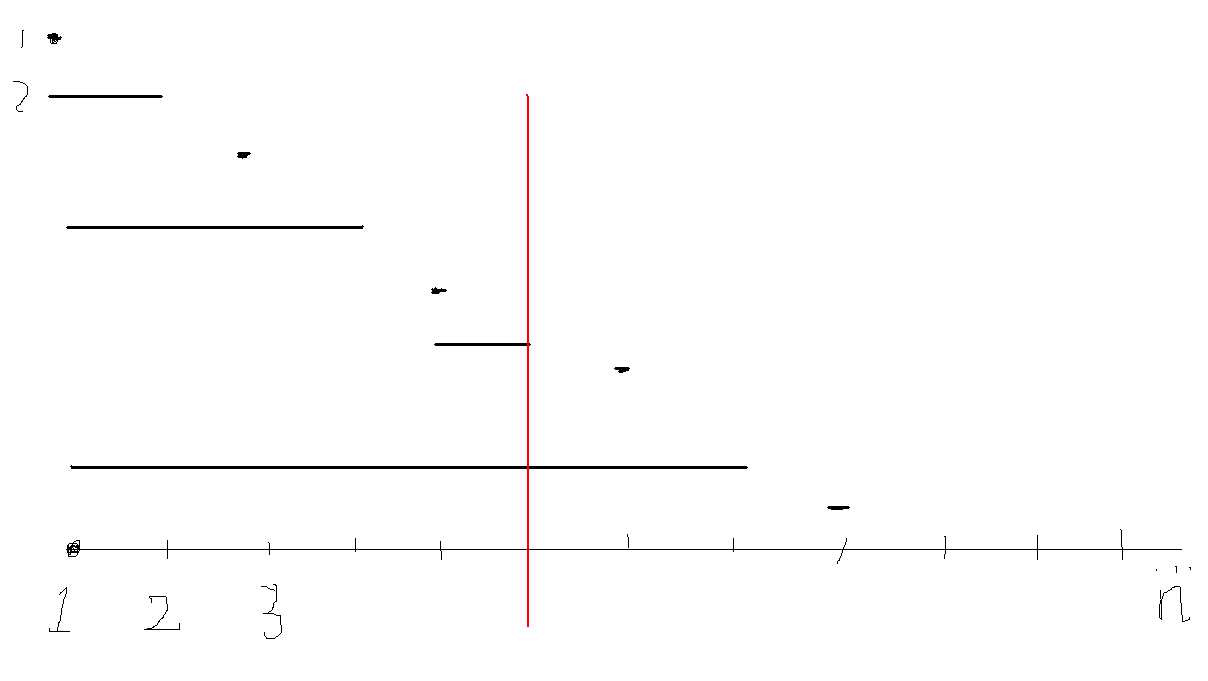
一种比较快的维护这个过程的方式是:
用这个位置更新每个区间时, 顺便用这个区间所包含的小区间去更新它, 这样就算小区间也包含了这个位置, 而小区间一定被提前更新过.

void updata(int x, int k) {
    while (x <= n) {
        h[x] = k;
        int low = lowbit(x);
        for (int i = 1; i < low; i <<= 1)
            h[x] = max(h[x], h[x - i]);
        x += lowbit(x);
    }       
}

区间查询

当然也不能直接用区间和的方式来查询.
因为一般区间和的写法是用前缀和的形式\(A_r - A_{l - 1}\)
而显然区间最值是不满足可减性的.

因此只要利用树状数组每个位置所维护的区间是\((x - lowbit_x, x)\)这条性质即可.

int query(int x, int y) {
    int ans = 0;
    while (y >= x)
    {
        ans = max(a[y], ans), y -= 1;
        for (; y-lowbit(y) >= x; y -= lowbit(y))
            ans = max(h[y], ans);
    }
    return ans;
}

树状数组维护区间最值

标签：lowbit   span   最大   前缀   维护   最大值   参考   直接   href   

原文地址：https://www.cnblogs.com/qdscwyy/p/9759220.html