标签:决定 微软 不同 西湖 替换 导数 14. 优点 交换
使用机器学习排序算法LambdaMART有一段时间了,但一直没有真正弄清楚算法中的所有细节。
学习过程中细读了两篇不错的博文,推荐给大家:
徐博From RankNet to LambdaRank to LambdaMART: An Overview
但经过一番搜寻之后发现,目前网上并没有一篇透彻讲解该算法的文章,所以希望这篇文章能够达到此目的。
本文主要参考微软研究院2010年发表的文章From RankNet to LambdaRank to LambdaMART: An Overview$^1$,并结合自己的理解,试图将RankNet、LambdaRank和LambdaMART这三种算法的所有算法细节讲解透彻。
RankNet、LambdaRank和LambdaMART是三个关系非常紧密的机器学习排序算法。简而言之,RankNet是最基础,基于神经网络的排序算法;而LambdaRank在RankNet的基础上修改了梯度的计算方式,也即加入了lambda梯度;LambdaMART结合了lambda梯度和MART(另称为GBDT,梯度提升树)。这三种算法在工业界中应用广泛,在BAT等国内大厂和微软谷歌等世界互联网巨头内部都有大量应用,还曾经赢得“Yahoo!Learning To Rank Challenge(Track 1)"的冠军。本人认为如果评选当今工业界中三种最重要的机器学习算法,以LambdaMART为首的集成学习算法肯定占有一席之地,另外两个分别是支持向量机和深度学习。
2.1 算法基础定义
RankNet解决如下搜索排序问题:给定query集合,每个query都对应着一个文档集合,如何对每个query返回排序后的文档集合。可以想象这样的场景:某位高考生在得知自己的成绩后,准备报考志愿。听说最近西湖大学办得不错,所以就想到网上搜搜关于西湖大学的资料。他打开一个搜索引擎,输入“西湖大学”四个字,然后点击“搜索”,页面从上到下显示了10条搜索结果,他认为排在上面的肯定比下面的相关,所以就开始从上往下一个个地浏览。所以RankNet的目标就是对所有query,都能将其返回的文档按照相关性进行排序。
RankNet网络将输入query的特征向量$x\in \mathbb{R}^n$映射为一个实数$f(x) \in \mathbb{R}$。RankNet采用pairwise的方法进行模型训练。具体地,给定特定query下的两个文档$U_i$和$U_j$,其特征向量分别为$x_i$和$x_j$,经过RankNet进行前向计算得到对应的分数为$s_i=f(x_i)$和$s_j=f(x_j)$。用$U_i \rhd U_j$表示$U_i$比$U_j$排序更靠前(如对某个query来说,$U_i$被标记为“good”,$U_j$被标记为“bad”)。继而可以用下面的公式来表示$U_i$应该比$U_j$排序更靠前的概率:$$P_{ij} \equiv P(U_i \rhd U_j) \equiv \frac{1}{1+e^{-\sigma(s_i-s_j)}}$$这个概率实际上就是深度学习中经常使用的sigmoid函数,参数$\sigma$决定sigmoid函数的形状。对于特定的query,定义$S_{ij} \in \{0,\pm1\}$为文档$i$和文档$j$被标记的标签之间的关联,即
$$ S_{ij}=\left\{
\begin{aligned}
1&& 文档i比文档j更相关\\
0&& 文档i和文档j相关性一致\\
-1&& 文档j比文档i更相关
\end{aligned}
\right.
$$
定义$\overline{P}_{ij}=\frac{1}{2}(1+S_{ij})$表示$U_i$应该比$U_j$排序更靠前的已知概率,则可以用交叉熵定义优化目标的损失函数:$$C=-\overline{P}_{ij}log{P_{ij}}-(1-\overline{P}_{ij})log(1-P_{ij})$$
如果不太熟悉什么是交叉熵,可以参考宗成庆老师的《统计自然语言处理》2.2节“信息论基本概念”,里面将熵、联合熵、互信息、相对熵、交叉熵和困惑度等概念都讲得相当清楚。
结合以上多个公式,可以改写损失函数$C$为:$$C=\frac{1}{2}(1-S_{ij})\sigma(s_i-s_j)+log(1+e^{-\sigma(s_i-s_j)})$$
对于$S_{ij}=1$,$$C=log\left(1+e^{-\sigma(s_i-s_j)}\right)$$
然而对于$S_{ij}=-1$,$$C=log\left(1+e^{-\sigma(s_j-s_i)}\right)$$
可以看出损失函数$C$具有对称性,也即交换$i$和$j$的位置,损失函数的值不变。
分析损失函数$C$的趋势发现,如果对文档$U_i$和$U_j$的打分可以正确地拟合标记的标签,则$C$趋向于0,否则$C$趋向于线性函数。具体地,假如$S_{ij}=1$,也即$U_i$应该比$U_j$排序高,如果$s_i>s_j$,则拟合的分数可以正确排序文档$i$和文档$j$,$$\lim \limits_{s_i-s_j\rightarrow\infty}C=\lim \limits_{s_i-s_j\rightarrow\infty}log\left(1+e^{-\sigma(s_i-s_j)}\right)=log1=0$$
如果$s_i<s_j$,则拟合的分数不能正确排序文档$i$和文档$j$,$$\lim \limits_{s_i-s_j\rightarrow\infty}C=\lim \limits_{s_i-s_j\rightarrow\infty}log\left(1+e^{-\sigma(s_i-s_j)}\right)=log\left(e^{-\sigma(s_i-s_j)}\right)=-\sigma(s_i-s_j)$$
利用神经网络对模型进行训练,目前最有效的方法就是反向传播算法。反向传播算法中最核心部分就是损失函数对模型参数的求导,然后可以使用下面的公式对模型参数进行迭代更新:
$$w_k\rightarrow{w_k}-\eta\frac{\partial{C}}{\partial{w_k}}={w_k}-\eta\left(\frac{\partial{C}}{\partial{s_i}}\frac{\partial{s_i}}{\partial{w_k}}+\frac{\partial{C}}{\partial{s_j}}\frac{\partial{s_j}}{\partial{w_k}}\right)$$
损失函数$C$对$s_i$和$s_j$的偏导数为:$$\frac{\partial{C}}{\partial{s_i}}=\sigma\left(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}}\right)=-\frac{\partial{C}}{\partial{s_j}}$$
$s_i$和$s_j$对$w_k$的偏导数可根据神经网络求偏导数的方式求得。求得了损失函数$C$对神经网络模型参数$w_k$的偏导数之后,就可以使用梯度下降算法对其更新。这里的学习率$\eta$也是一个正数,因为$\eta$需要满足下面的不等式:$$\delta C=\sum_{k}\frac{\partial{C}}{\partial{w_k}}\delta w_k=\sum_{k}\frac{\partial{C}}{\partial{w_k}}\left(-\eta\frac{\partial{C}}{\partial{w_k}}\right)=-\eta\sum_{k}\left(\frac{\partial{C}}{\partial{w_k}}\right)^2<0$$
2.2 RankNet分解形式:加速RankNet训练过程
2.1节中定义的RankNet,对于每一个文档对$(U_i$,$U_j)$都将计算损失函数对神经网络的参数$w_k$的偏导数,然后更新模型参数$w_k$。这样做的缺点在于,对模型参数更新慢,耗时长。所以本节讲解如何通过分解组合的方式加快这一训练过程。
对于给定的文档对$U_i$和$U_j$,损失函数$C$对参数$w_k$的偏导数为:$$\frac{\partial{C}}{\partial{w_k}}=\frac{\partial{C}}{\partial{s_i}}\frac{\partial{s_i}}{\partial{w_k}}+\frac{\partial{C}}{\partial{s_j}}\frac{\partial{s_j}}{\partial{w_k}}=\sigma\left(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}}\right)\left(\frac{\partial{s_i}}{\partial{w_k}}-\frac{\partial{s_j}}{\partial{w_k}}\right)=\lambda_{ij}\left(\frac{\partial{s_i}}{\partial{w_k}}-\frac{\partial{s_j}}{\partial{w_k}}\right)$$
其中:$$\lambda_{ij}=\frac{\partial{C(s_i-s_j)}}{\partial{s_i}}=\sigma\left(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}}\right)$$
定义$I$为索引对$\{i,j\}$的集合,在不损失信息量的情况下,可以将集合$I$中的索引对都转换成满足$U_i \rhd U_j$的形式。另外集合$I$中的索引对还应该满足最多只出现一次的条件。在此基础上,累加权重参数$w_k$的更新量:$$\delta w_k=-\eta\sum_{(i,j) \in I}\left(\lambda_{ij}\frac{\partial{s_i}}{\partial{w_k}}-\lambda_{ij}\frac{\partial{s_j}}{\partial{w_k}}\right)=-\eta\sum_{i}\lambda_i\frac{\partial{s_j}}{\partial{w_k}}$$
其中:$$\lambda_i=\sum_{j:\{i,j\} \in I}\lambda_{ij}-\sum_{j:\{j,i\} \in I}\lambda_{ij}$$
通俗地说,$\lambda_i$就是集合$I$中所有$\{i,j\}$的$\lambda_{ij}$的和$-$集合$I$中所有$\{j,i\}$的$\lambda_{ij}$的和。如果还是不太明白,那看下面这个例子就明白了。集合$I=\{\{1,2\},\{2,3\},\{1,3\}\}$,则
$$\delta w_k=-\eta\sum_{\{i,j\}\in I}\left(\lambda_{ij}\frac{\partial{s_i}}{\partial{w_k}}-\lambda_{ij}\frac{\partial{s_j}}{\partial{w_k}}\right)=-\eta\left(\lambda_{12}\frac{\partial{s_1}}{\partial{w_k}}-\lambda_{12}\frac{\partial{s_2}}{\partial{w_k}}+\lambda_{13}\frac{\partial{s_1}}{\partial{w_k}}-\lambda_{13}\frac{\partial{s_3}}{\partial{w_k}}+\lambda_{23}\frac{\partial{s_2}}{\partial{w_k}}-\lambda_{23}\frac{\partial{s_3}}{\partial{w_k}}\right)=-\eta\left((\lambda_{12}+\lambda_{13})\frac{\partial{s_1}}{\partial{w_k}}+(\lambda_{23}-\lambda_{12})\frac{\partial{s_2}}{\partial{w_k}}+(-\lambda_{23}-\lambda_{13})\frac{\partial{s_3}}{\partial{w_k}}\right)$$
于是可以得到$\lambda_1=\lambda_{12}+\lambda_{13}$,$\lambda_2=\lambda_{23}-\lambda_{12}$,$\lambda_3=-\lambda_{23}-\lambda_{13}$
$\lambda_i$可以看成是作用在排序文档上的力,其正负代表了方向,长度代表了力的大小。最初的实现是对每个文档对,都计算一遍梯度并且更新神经网络的参数值,而这里则是将同一个query下的所有文档对进行叠加,然后更新一次网络的权重参数。这种分解组合形式实际上就是一种小批量学习方法,不仅可以加快迭代速度,还可以为后面使用非连续的梯度模型打下基础。
2.3 模型训练过程示例
假设某个搜索系统中,文档用2维的特征向量表示。给定一个query下的三个文档向量分别为$x_1=(5,4.5)^T$,$x_2=(4,3.7)^T$和$x_3=(2,1.8)^T$,标记情况为$U_1 \rhd U_2 \rhd U_3$。为了简化训练过程,这里采用单层的神经网络模型,即输入层大小2,输出层大小为1,输出值为$f(x)=w_0+w_1x^{(1)}+w_2x^{(2)}$。
初始化$\mathbf{w}=[0, -1, 1]$,控制sigmoid函数形状的$\sigma=0.1$,神经网络学习率$\eta=0.1$。
根据以上初始值可以计算出$s_1=-0.5$,$s_2=-0.3$和$s_3=-0.2$,可见此时三个文档输出的分数并不满足标记$U_1 \rhd U_2 \rhd U_3$。
计算$\lambda_1=\lambda_{12}+\lambda_{13}=-0.1012$,$\lambda_2=\lambda_{23}-\lambda_{12}=0.0002$,$\lambda_3=-\lambda_{23}-\lambda_{13}=-0.1010$。
$\delta w_0=-\eta\left(\lambda_1\frac{\partial{s_1}}{\partial{w_0}}+\lambda_2\frac{\partial{s_2}}{\partial{w_0}}+\lambda_3\frac{\partial{s_3}}{\partial{w_0}}\right)=0$
$\delta w_1=-\eta\left(\lambda_1\frac{\partial{s_1}}{\partial{w_1}}+\lambda_2\frac{\partial{s_2}}{\partial{w_1}}+\lambda_3\frac{\partial{s_3}}{\partial{w_1}}\right)=3.032$
$\delta w_2=-\eta\left(\lambda_1\frac{\partial{s_1}}{\partial{w_2}}+\lambda_2\frac{\partial{s_2}}{\partial{w_2}}+\lambda_3\frac{\partial{s_3}}{\partial{w_2}}\right)=2.7286$
更新网络权重:
$w_0=w0+\delta w_0=0+0=0$
$w_1=w1+\delta w_1=-1+3.032=2.032$
$w_2=w2+\delta w_2=1+2.7286=3.7286$
使用更新后的权重重新计算三个文档的分数,分别为$s_1=26.9387$,$s_2=21.92382$,$s_3=10.77548$。可见,经过一轮训练,单层神经网络的输出分数已经可以很好地拟合标记的标签。
信息检索研究者经常使用的排序质量评分指标有以下四种:
MRR(Mean Reciprocal Rank),平均倒数排名
MAP(Mean Average Precision),平均正确率均值
NDCG(Normalized Discounted Cumulative Gain),归一化折损累积增益
ERR(Expected Reciprocal Rank),预期倒数排名
其中,MRR和MAP只能对二级的相关性(排序等级:相关和不相关)进行评分,而NDCG和ERR则可以对多级的相关性(排序等级>2)进行评分。NDCG和ERR的另一个优点是更关注排名靠前的文档,在计算分数时会给予排名靠前的文档更高的权重。但是这两种评分方式的缺点是函数不连续,不能进行求导,所以也就不能简单地将这两种评分方式加入到模型的损失函数中去。
3.1 MRR
对于一个查询$i$来说,$rank_i$表示第一个相关结果的排序位置,所以:$$MRR(Q)=\frac{1}{|Q|}\sum_{i=1}^{|Q|}\frac{1}{rank_i}$$
$|Q|$表示查询的数量,$MRR$表示搜索系统在查询集$Q$下的平均倒数排名值。$MRR$只能度量检索结果只有一个并且相关性等级只有相关和不相关两种的情况。
举个简单例子:
| 查询语句 | 查询结果 | 正确结果 | 排序位置 | 排序倒数 |
| 机器学习 | 快速排序,深度学习,并行计算 | 深度学习 | 2 | 1/2 |
| 苹果手机 | 小米手机,华为手机,iphone 7 | iphone 7 | 3 | 1/3 |
| 小米移动电源 | 小米移动电源,华为充电器,苹果充电插头 | 小米移动电源 | 1 | 1/1 |
所以$MRR(Q)=\frac{1/2+1/3+1}{3}=\frac{11}{18}$
3.2 MAP
假定信息需求$q_j \in Q$对应的所有相关文档集合为${d_{1},...,d_{mj}}$,$R_{jk}$是返回结果中直到遇到$d_k$后其所在位置前(含$d_k$)的所有文档的集合,则定义$MAP(Q)^2$如下:
$$MAP(Q)=\frac{1}{|Q|}\sum_{j=1}^{|Q|}\frac{1}{m_j}\sum_{k=1}^{m_j}Precision(R_{jk})$$
实际上有两种计算$MAP$的方法或者说有两种$MAP(Q)$的定义方法。第一种方法是在每篇相关文档所在位置上求正确率然后平均(参考上面的公式)。另一种是在每个召回率水平上计算此时的插值正确率,然后求11点平均正确率,最后在不同查询之间计算平均。前者也称为非插值$MAP(Q)$。一般提$MAP(Q)$都指前者,所有这里也只讨论前者。
如果对定义的公式不太理解,可以结合下面的例子进行理解。
| 查询1:机器学习 | 查询2:苹果手机 | ||
| 排序位置 | 是否相关 | 排序位置 | 是否相关 |
| 1 | 是 | 1 | 否 |
| 2 | 是 | 2 | 是 |
| 3 | 否 | 3 | 是 |
| 4 | 否 | 4 | 否 |
| 5 | 是 | 5 | 否 |
| 6 | 否 | 6 | 是 |
| 7 | 否 | 7 | 是 |
针对上面检索的结果,可计算出
$AP(1)=\left(1*1+1*1+2/3*0+2/4*0+3/5*1+3/6*0+3/7*0\right)/3=\frac{13}{15}$
$AP(2)=\left(0*0+1/2*1+2/3*1+2/4*0+2/5*0+3/6*1+4/7*1\right)/4=\frac{47}{84}$
$MAP(Q)=\frac{AP(1)+AP(2)}{2}=\frac{13/15+47/84}{2}=\frac{599}{420}$
3.3 NDCG
NDCG是基于前$k$个检索结果进行计算的。设$R(j,m)$是评价人员给出的文档$d$对查询$j$的相关性得分,那么有:
$$NDCG(Q,k)=\frac{1}{|Q|}\sum_{j=1}^{|Q|}Z_{j,k}\sum_{m=1}^{k}\frac{2^{R(j,m)}-1}{log(1+m)}$$
其中$$DCG_k=\sum_{m=1}^{k}\frac{2^{R(j,m)}-1}{log(1+m)}$$
$Z_{j,k}$为第$j$个查询的DCG归一化因子,用于保证对于查询$j$最完美系统的$DCG_k$得分是1。$Z_{j,k}$也可以用$\frac{1}{IDCG_k}$表示。$m$是返回文档的位置。如果某查询返回的文档数$k‘<k$,那么上述公式只需要计算到$k‘$为止。
修改上面简单的例子进行辅助理解:
| 查询1:机器学习 | 查询2:苹果手机 | ||
| 排序位置 | 相关程度 | 排序位置 | 相关程度 |
| 1 | 3 | 1 | 2 |
| 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 |
| 4 | 0 | 4 | 1 |
| 5 | 1 | 5 | 2 |
| 6 | 2 | 6 | 3 |
| 7 | 2 | 7 | 1 |
对于查询1:机器学习:
$$DCG_7=\sum_{m=1}^{7}\frac{2^{R(j,m)}-1}{log(1+m)}=21.421516$$
查询1返回结果的最佳相关程度排序为:3,3,2,2,2,1,0,所以,$IDCG_7=22.686817$,$NDCG_7=\frac{DCG_7}{IDCG_7}=0.944227$
对于查询2:苹果手机:
$$DCG_7=\sum_{m=1}^{7}\frac{2^{R(j,m)}-1}{log(1+m)}=18.482089$$
查询2返回结果的最佳相关程度排序为:3,3,2,2,2,1,1,所以,$IDCG_7=23.167716$,$NDCG_7=\frac{DCG_7}{IDCG_7}=0.797752$
最后可得:$NDCG(Q,7)=(0.944227+0.797752)/2=0.870990$
3.4 ERR
$ERR^3$旨在改善NDCG计算当前结果时未考虑排在前面结果的影响的缺点,提出了一种基于级联模型的评价指标。首先定义:
$$R(g)=\frac{2^g-1}{2^{g_{max}}}, g \in \{0,1,...,g_{max}\}$$
$g$代表文档的得分级别,$g_{max}$代表最大的分数级别。
于是定义:
$$ERR=\sum_{r=1}^{n}\frac{1}{r}\prod_{i=1}^{r-1}(1-R_i)R_r$$
展开公式如下:
$$ERR=R_1+\frac{1}{2}(1-R_1)R_2+\frac{1}{3}(1-R_1)(1-R_2)R_3+...+\frac{1}{n}(1-R_1)(1-R_2)...(1-R_{n-1})R_n$$
举例来说($g_{max}=3$):
| 查询:机器学习 | |
| 排序位置 | 相关程度 |
| 1 | 3 |
| 2 | 2 |
| 3 | 3 |
| 4 | 1 |
$R_1=0.875,R2=0.375,R_3=0.875,R_4=0.125$
$ERR=0.875+\frac{1}{2}*0.125*0.375+\frac{1}{3}*0.125*0.625*0.875+\frac{1}{4}*0.125*0.625*0.125*0.125=0.913391$
4.1 为什么需要LambdaRank
先看一张论文原文中的图,如下所示。这是一组用二元等级相关性进行排序的链接地址,其中浅灰色代表链接与query不相关,深蓝色代表链接与query相关。 对于左边来说,总的pairwise误差为13,而右边总的pairwise误差为11。但是大多数情况下我们更期望能得到左边的结果。这说明最基本的pairwise误差计算方式并不能很好地模拟用户对搜索引擎的期望。右边黑色箭头代表RankNet计算出的梯度大小,红色箭头是期望的梯度大小。NDCG和ERR在计算误差时,排名越靠前权重越大,可以很好地解决RankNet计算误差时的缺点。但是NDCG和ERR均是不可导的函数,如何加入到RankNet的梯度计算中去?
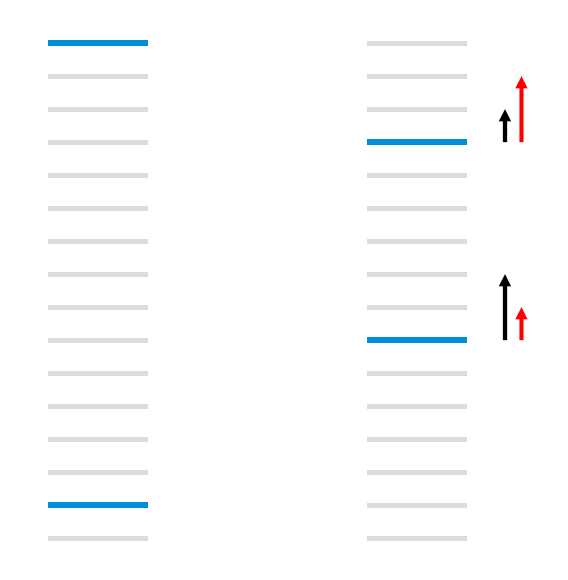
4.2 LambdaRank定义
RankNet中的$\lambda_{ij}$可以看成是$U_i$和$U_j$中间的作用力,如果$U_i \rhd U_j$,则$U_j$会给予$U_i$向上的大小为$|\lambda_{ij}$的推动力,而对应地$U_i$会给予$U_j$向下的大小为$|\lambda_{ij}$的推动力。如何将NDCG等类似更关注排名靠前的搜索结果的评价指标加入到排序结果之间的推动力中去呢?实验表明,直接用$|\Delta_{NDCG}|$乘以原来的$\lambda_{ij}$就可以得到很好的效果,也即:
$$\lambda_{ij}=\frac{\partial{C(s_i-s_j)}}{\partial{s_i}}=\frac{-\sigma}{1+e^{\sigma(s_i-s_j)}}|\Delta_{NDCG}|$$
其中$|\Delta_{NDCG}|$是交换排序结果$U_i$和$U_j$得到的NDCG差值。NDCG倾向于将排名高并且相关性高的文档更快地向上推动,而排名地而且相关性较低的文档较慢地向上推动。
另外还可以将$|\Delta_{NDCG}|$替换成其他的评价指标。
5.1 MART
LambdaMART是MART和LambdaRank的结合,所以要学习LambdaMART首先得了解什么是MART。MART是Multiple Additive Regession Tree的简称,很多时候又称为GBDT(Gradient Boosting Decision Tree)。MART是一种集成学习算法,不同于经典的集成学习算法Adaboost利用前一轮学习器的误差来更新下一轮学习的样本权重,MART每次都拟合上一轮分类器产生的残差。举个例子便于理解,比如一个人的年龄是50岁,第一棵树拟合的结果是35岁,第一轮的残差为15岁;然后第二棵数拟合的结果是10岁,两棵树相加总的拟合结果是45岁,第二轮的残差为5岁;第三棵数拟合的结果为2岁,三棵树相加拟合的结果是47岁,第三轮的残差是3岁......只要如此不断地进行下去,拟合结果就可以达到50岁,拟合残差的过程就是训练数据的过程。
对于一个给定的数据集$\{x_i,y_i\}, i=1,2,...,m$,其中特征向量$x_i \in \mathbb{R}^n$,标签$y_i \in \mathbb{R}$,可以用$x_{ij}, j=1,2,...,d来代表x_i的第j个特征值$。对于一个典型的回归决策树问题,需要遍历所有特征$j$的全部阈值$t$,找到最优的$j$和$t$使下面的等式最小化:
$$S_j=\sum_{i \in L}(y_i-\mu_L)^2+\sum_{i \in R}(y_i-\mu_R)^2$$
其中$x_{ij} \leq t$的所有样本落入左子树$L$中,其中$x_{ij} > t$的所有样本落入右子树$R$中,$\mu_L(\mu_R)$表示左子树(右子树)所有样例标签值的均值。如果这就是一棵最简单的拥有一个根节点、两个叶子节点的二叉回归树,那么只需要根据最优阈值切分为左右子树,并且分别计算左右子树的值$\gamma_l,l=1,2$即可。如果将划分子树的过程继续进行$L-1$次即可得到一棵包含$L$个叶子节点的回归树。
上面公式使用最小二乘法计算拟合误差,所以通过上面方法得到的模型又称为最小二乘回归树。其实不管误差的计算方式如何,我们都可以拟合出相应的回归树,唯一的区别是梯度的计算不同而已。
MART使用线性组合的方式将拟合的树结合起来,作为最后的输出:
$$F_n(x)=\sum_{i=1}^{N}\alpha_if_i(x)$$
$f_i(x)$是单棵回归树函数,$\alpha_i$是第$i$棵回归树的权重。
在这里我们需要弄清楚为什么拟合残差就能不断减少拟合误差。假设拟合误差$C$是拟合函数$F_n$的函数$C(F_n)$。那么:
$$\delta C \approx \frac{\partial{C(F_n)}}{\partial{F_n}}\delta F_n$$
如果取$\delta F_n=-\eta \frac{\partial{C}}{\partial{F_n}}$,就可以得到$\delta C<0$。其中$\eta$是学习率,为正实数。所以只要函数$F_n$拟合误差函数的负梯度就可以不断降低拟合误差的值。
设标签向量$y=[y_1,y_2,...,y_m]^T$,如果用最小二乘的方式表示拟合误差,则:$$C=\frac{1}{2}(F_n-y)^2$$
那么$\delta F_n=-\eta \frac{\partial{C}}{\partial{F_n}}=-\eta (F_n-y)$。这其实就是上面提到的残差,所以拟合残差可以不断减少拟合误差。
5.2 逻辑回归+MART进行二分类
了解了MART之后,下面举一个MART实际应用的例子:使用MART和逻辑回归进行二分类。用于分类的样本$x_i \in \mathbb{R}^n$,标签$y_i \in \{\pm1\}$,拟合函数$F(x)$。为了简化表示,我们表示条件概率如下:
$$P_+ \equiv P(y=1|x)$$
$$P_- \equiv P(y=-1|x)$$
用交叉熵表示损失函数:$$L(y,F)=-ylog(P_+)-(1-y)log(P_-)$$
逻辑回归使用对数机率(属于正例概率/属于负例概率)进行建模,
$$F_n(x)=\frac{1}{2}log(\frac{P_+}{P_-})$$
$$P_+=\frac{1}{1+e^{-2\sigma F_n(x)}}$$
$$P_-=1-P_+=\frac{1}{1+e^{2\sigma F_n(x)}}$$
将$P_+$和$P_-$带入$L(y,F)$中,得到:
$$L(y,F_n)=log(1+e^{-2y\sigma F_n})$$
$R_{jm}$表示落入第$m$棵树的第$j$个叶子节点中的样例集合,可以通过下式对该叶子节点的值进行优化:
$$\gamma_{jm}=arg\min_{\gamma}\sum_{x_i \in R_{jm}}\log\left(1+e^{-2\sigma y_i\left(F_{m-1}\,\,\left({x_i}\right)+\gamma\right)\,}\right)$$
上式可以使用Newton-Raphson方法按照下面的公式进行迭代求解:
$$\gamma_{n+1}=\gamma_{n}-\frac{g‘(\gamma_n)}{g‘‘(\gamma_n)}$$
5.3 LambdaMART基本定义
LambdaMART基于MART,优化$\lambda$梯度。根据上面的定义,对于任意$U_i$和$U_j$,有:
$$\lambda_{ij}=\frac{\partial{C(s_i-s_j)}}{\partial{s_i}}=\frac{-\sigma |\Delta_{Z_{ij}}|}{1+e^{\sigma(s_i-s_j)}}$$
$|\Delta_{Z_{ij}}|$表示交换$U_i$和$U_j$的位置产生的评价指标差值,$Z$可以是$NDCG$或者$ERR$等。对于特定$U_i$,累加其他所有排序项的影响,得到:
$$\lambda_i=\sum_{j:\{i,j\} \in I}\lambda_{ij}-\sum_{j:\{j,i\} \in I}\lambda_{ij}$$
为了简化表示:
$$\sum_{\{i,j\}\rightleftharpoons I}=\sum_{j:\{i,j\} \in I}\lambda_{ij}-\sum_{j:\{j,i\} \in I}\lambda_{ij}$$
于是我们可以更新损失函数:
$$\frac{\partial{C}}{\partial{s_i}} = \sum_{j:\{i,j\} \in I} \frac{-\sigma |\Delta_{Z_{ij}}|}{1+e^{\sigma(s_i-s_j)}} = \sum_{j:\{i,j\} \in I} -\sigma |\Delta_{Z_{ij}}| \rho_{ij}$$
其中,我们定义:
$$\rho_{ij}=\frac{1}{1+e^{\sigma(s_i-s_j)}}=\frac{-\lambda_{ij}}{\sigma |\Delta_{Z_{ij}}|}$$
然后可以得到:
$$\frac{\partial{^2C}}{\partial{s_i^2}}=\sum_{\{i,j\}\rightleftharpoons I}\sigma^2|\Delta_{Z_{ij}}|\rho{ij}(1-\rho_{ij})$$
所以我们可以用下面的公式计算第$k$棵树的第$k$个叶子节点上的值:
$$\gamma_{km}=\frac{\sum_{x_i \in R_{km}}\frac{\partial{C}}{\partial{s_i}}}{\sum_{x_i \in R_{km}}\frac{\partial{^2C}}{\partial{s_i^2}}}=\frac{-\sum_{x_i \in R_{km}}\sum_{\{i,j\}\rightleftharpoons I}|\Delta_{Z_{ij}}|\rho_{ij}}{\sum_{x_i \in R_{km}}\sum_{\{i,j\}\rightleftharpoons I}|\Delta_{Z_{ij}}|\rho_{ij}(1-\rho_{ij})}$$
所以总结LambdaMART算法如下:

1. Christopher J.C. Burges. From RankNet to LambdaRank to LambdaMART: An Overview. Microsoft Research Technical Report MSR-TR-010-82.
2. Chrisopher D.Manning, Prabhakar Raghavan, Hinrich Schutze著, 王斌译. Introduction to Information Retrieval, 8.4 有序检索结果的评价方法, 2017年10月北京第11次印刷.
3. Olivier Chapelle, Ya Zhang, Pierre Grinspan. Expected Recipocal Rank for Graded Relevance. CIKM 2009.
机器学习排序算法:RankNet to LambdaRank to LambdaMART
标签:决定 微软 不同 西湖 替换 导数 14. 优点 交换
原文地址:https://www.cnblogs.com/genyuan/p/9788294.html