标签:设定 线性 com 网络 文章 网格 操作 图像 相对
目录
@
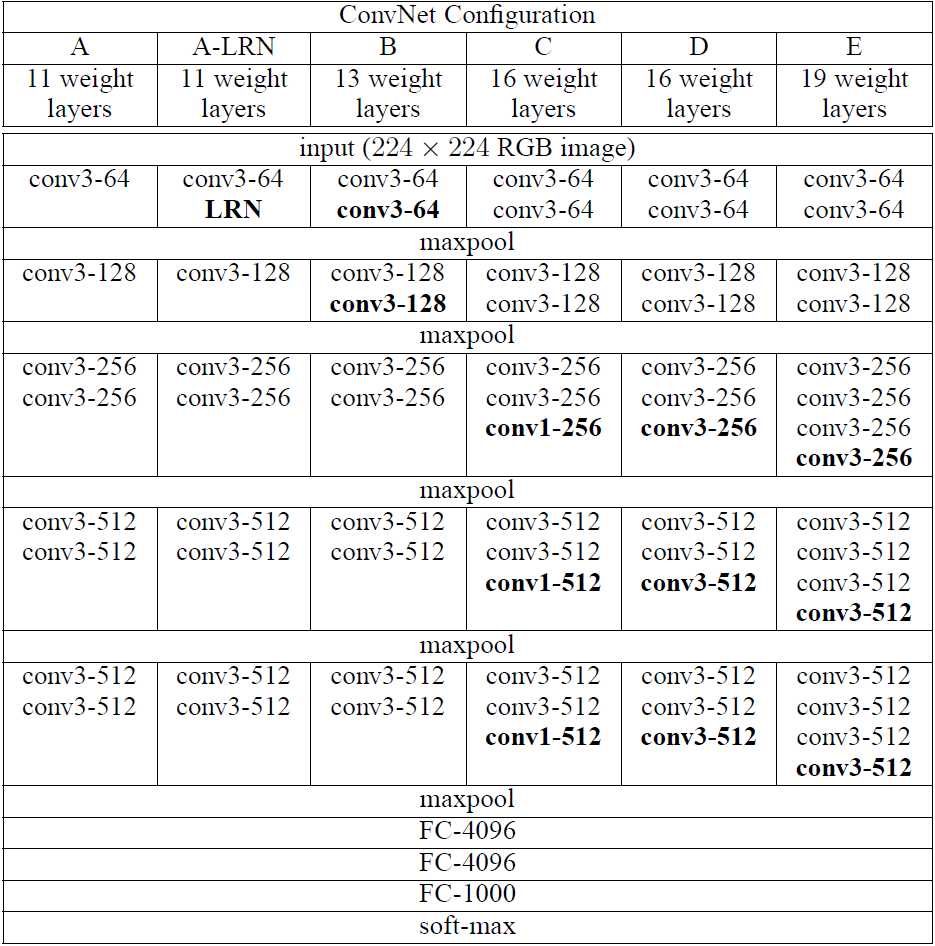
??VGG提出了相对AlexNet更深的网络模型,并且通过实验发现网络越深性能越好(在一定范围内)。在网络中,使用了更小的卷积核(3x3),stride为1,同时不单单的使用卷积层,而是组合成了“卷积组”,即一个卷积组包括2-4个3x3卷积层(a stack of 3x3 conv),有的层也有1x1卷积层,因此网络更深,网络使用2x2的max pooling,在full-image测试时候把最后的全连接层(fully-connected)改为全卷积层(fully-convolutional net),重用训练时的参数,使得测试得到的全卷积网络因为没有全连接的限制,因而可以接收任意宽或高为的输入,另外VGGNet卷积层有一个显著的特点:特征图的空间分辨率单调递减,特征图的通道数单调递增,这是为了更好地将HxWx3(1)的图像转换为1x1xC的输出,之后的GoogLeNet与Resnet都是如此。另外上图后面4个VGG训练时参数都是通过pre-trained 网络A进行初始赋值。上图为VGG不同版本的网络模型,较为流行的是VGG-16,与VGG-19。
??另外在某篇博客看到一段对VGG-Net与GoogLe-Net的总结,摘取至此(会在最后的参考链接给出引用):
GoogLeNet和VGG的Classification模型从原理上并没有与传统的CNN模型有太大不同。大家所用的Pipeline也都是:训练时候:各种数据Augmentation(剪裁,不同大小,调亮度,饱和度,对比度,偏色),剪裁送入CNN模型,Softmax,Backprop。测试时候:尽量把测试数据又各种Augmenting(剪裁,不同大小),把测试数据各种Augmenting后在训练的不同模型上的结果再继续Averaging出最后的结果。
??使用3x3小卷积核,是能够获取上下左右中心信息的最小卷积核,同时在某些“卷积组”使用1x1卷积核,stride=1,padding=1(为了保证卷积层后像素保持不变),2个3x3卷积层堆叠起来相当于一个5x5卷积层,3个3x3卷积层堆叠起来相当于一个7x7卷积层。但一些3x3卷积层堆叠起来与直接一个7x7卷积层有什么好处呢?作者给出了如下几个理由:
??1x1卷积核是在保持空间维度不变的情况下,进行了一个线性映射并且多加上了一层非线性修正层,是一种增加决策函数“非线性”(non-linearity)而不影响卷积层感受野的方式。
??相对于AlexNet使用的3x3池化核,VGG使用2x2池化核,stride为2的max pooling,从而获取更细节的信息。
??VGG最后三个全连接层在形式上完全平移AlexNet的最后三层,VGGNet后面三层(三个全连接层)为:
??在某个测试阶段(whole-image)作者将FC层利用conv层代替,如下图(上半部分是训练阶段,此时最后三层都是全连接层(输出分别是4096、4096、1000),下半部分是测试阶段(输出分别是1x1x4096、1x1x4096、1x1x1000),最后三层都是卷积层):
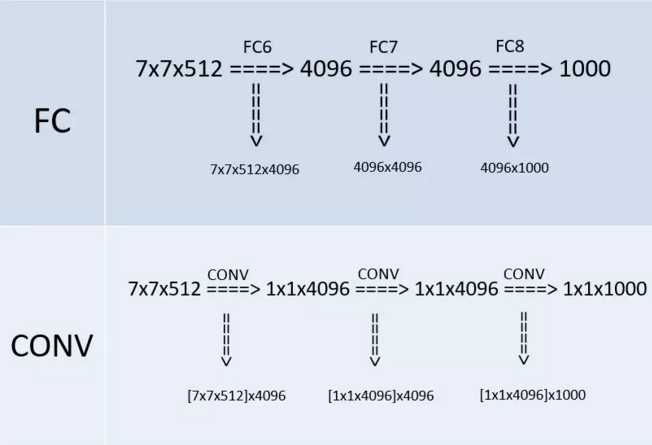
改变之后,整个网络由于没有了全连接层,网络中间的feature map不会固定,所以网络对任意大小的输入都可以处理。
ps:以下来自翻译,因为刚入门,对于训练/测试模型的一些操作还不是很熟悉,所以直接翻译了,积累一些训练方法跟trick。
??ConvNet训练过程通常遵循Krizhevsky等人(2012)(除了从多尺度训练图像中对输入裁剪图像进行采样外,如下文所述)。也就是说,通过使用具有动量的小批量梯度下降(基于反向传播(LeCun等人,1989))优化多项式逻辑回归目标函数来进行训练。批量大小设为256,动量为0.9。训练通过权重衰减(L2惩罚乘子设定为)进行正则化,前两个全连接层执行丢弃正则化(丢弃率设定为0.5)。学习率初始设定为,然后当验证集准确率停止改善时,减少10倍。学习率总共降低3次,学习在37万次迭代后停止(74个epochs)。我们推测,尽管与(Krizhevsky等,2012)相比我们的网络参数更多,网络的深度更大,但网络需要更小的epoch就可以收敛,这是由于(a)由更大的深度和更小的卷积滤波器尺寸引起的隐式正则化,(b)某些层的预初始化。
??网络权重的初始化是重要的,因为由于深度网络中梯度的不稳定,不好的初始化可能会阻碍学习。为了规避这个问题,我们开始训练配置A(表1),足够浅以随机初始化进行训练。然后,当训练更深的架构时,我们用网络A的层初始化前四个卷积层和最后三个全连接层(中间层被随机初始化)。我们没有减少预初始化层的学习率,允许他们在学习过程中改变。对于随机初始化(如果应用),我们从均值为0和方差为的正态分布中采样权重。偏置初始化为零。值得注意的是,在提交论文之后,我们发现可以通过使用Glorot&Bengio(2010)的随机初始化程序来初始化权重而不进行预训练。
??为了获得固定大小的224×224 ConvNet输入图像,它们从归一化的训练图像中被随机裁剪(每个图像每次SGD迭代进行一次裁剪)。为了进一步增强训练集,裁剪图像经过了随机水平翻转和随机RGB颜色偏移(Krizhevsky等,2012)。下面解释训练图像归一化。
??训练图像大小。令S是等轴归一化的训练图像的最小边,ConvNet输入从S中裁剪(我们也将S称为训练尺度)。虽然裁剪尺寸固定为224×224,但原则上S可以是不小于224的任何值:对于,裁剪图像将捕获整个图像的统计数据,完全扩展训练图像的最小边;对于,裁剪图像将对应于图像的一小部分,包含小对象或对象的一部分。
??我们考虑两种方法来设置训练尺度S。第一种是修正对应单尺度训练的S(注意,采样裁剪图像中的图像内容仍然可以表示多尺度图像统计)。在我们的实验中,我们评估了以两个固定尺度训练的模型:(已经在现有技术中广泛使用(Krizhevsky等人,2012;Zeiler&Fergus,2013;Sermanet等,2014))和。给定ConvNet配置,我们首先使用来训练网络。为了加速网络的训练,用预训练的权重来进行初始化,我们使用较小的初始学习率。
??设置S的第二种方法是多尺度训练,其中每个训练图像通过从一定范围(我们使用和)随机采样S来单独进行归一化。由于图像中的目标可能具有不同的大小,因此在训练期间考虑到这一点是有益的。这也可以看作是通过尺度抖动进行训练集增强,其中单个模型被训练在一定尺度范围内识别对象。为了速度的原因,我们通过对具有相同配置的单尺度模型的所有层进行微调,训练了多尺度模型,并用固定的进行预训练。
??在测试时,给出训练的ConvNet和输入图像,它按以下方式分类。首先,将其等轴地归一化到预定义的最小图像边,表示为Q(我们也将其称为测试尺度)。我们注意到,Q不一定等于训练尺度S(正如我们在第4节中所示,每个S使用Q的几个值会导致性能改进)。然后,网络以类似于(Sermanet等人,2014)的方式密集地应用于归一化的测试图像上。即,全连接层首先被转换成卷积层(第一FC层转换到7×7卷积层,最后两个FC层转换到1×1卷积层)。然后将所得到的全卷积网络应用于整个(未裁剪)图像上。结果是类得分图的通道数等于类别的数量,以及取决于输入图像大小的可变空间分辨率。最后,为了获得图像的类别分数的固定大小的向量,类得分图在空间上平均(和池化)。我们还通过水平翻转图像来增强测试集;将原始图像和翻转图像的soft-max类后验进行平均,以获得图像的最终分数。
??由于全卷积网络被应用在整个图像上,所以不需要在测试时对采样多个裁剪图像(Krizhevsky等,2012),因为它需要网络重新计算每个裁剪图像,这样效率较低。同时,如Szegedy等人(2014)所做的那样,使用大量的裁剪图像可以提高准确度,因为与全卷积网络相比,它使输入图像的采样更精细。此外,由于不同的卷积边界条件,多裁剪图像评估是密集评估的补充:当将ConvNet应用于裁剪图像时,卷积特征图用零填充,而在密集评估的情况下,相同裁剪图像的填充自然会来自于图像的相邻部分(由于卷积和空间池化),这大大增加了整个网络的感受野,因此捕获了更多的上下文。虽然我们认为在实践中,多裁剪图像的计算时间增加并不足以证明准确性的潜在收益,但作为参考,我们还在每个尺度使用50个裁剪图像(5×5规则网格,2次翻转)评估了我们的网络,在3个尺度上总共150个裁剪图像,与Szegedy等人(2014)在4个尺度上使用的144个裁剪图像。
??文章最后还有单尺度评估与多尺度评估,多裁剪图像评估等,这里就不细说了。
https://blog.csdn.net/abc_138/article/details/80568450
https://blog.csdn.net/qq_31531635/article/details/71170861
https://blog.csdn.net/qq_26591517/article/details/81071393
https://blog.csdn.net/u011440696/article/details/77756776
http://blog.leanote.com/post/dataliu/5d29e67dd0b0
标签:设定 线性 com 网络 文章 网格 操作 图像 相对
原文地址:https://www.cnblogs.com/kk17/p/9792071.html