标签:技术分享 sig 通过 char* str 探讨 连续 入口 应用
要求:
1.输入一个二维整形数组,数组里有正数也有负数。
2.二维数组中连续的一个子矩阵组成一个子数组,每个子数组都有一个和。
3.求所有子数组的和的最大值,要求时间复杂度为O(n)。
设计思路:
参照一维整数数组求解最大子数组的方法,通过将不同行列的最大子数和加起来的方法来求解整体最大子数组的和。
实现方法:先求出每一行的最大子数组之和,之后通过比较得出最大和MaxSum,然后通过上述方法求二行的最大子数组之和并与MaxSum比较,用MaxSum存放较大值。以此类推,再求第三行,第四行。。。
最后输出。
合作过程:
两人合作探讨设计思路。
一人负责分析程序,编写代码。
另一人负责代码复审和代码测试。
主要代码:
// 2w.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
int _tmain(int argc, _TCHAR* argv[])
{
return 0;
}
//二维整数数组最大子数组之和
#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;
int main()
{
int E,F;
cout << "输入二维数组的行数和列数:" << endl;
cin >> E >> F;
int a[5][5],line[5],sum = 0,d1 = 0;
int MaxSum ,Maxd1,end1[5][5] = {0},end2[5][5] = {0};
int i_max = 0,j_max = 0;
srand((unsigned int)time(0));
cout << "二维数组为:" << endl;
for (int j = 0;j < E;j++)
{
for (int k = 0;k < F;k++)
{
a[j][k] = rand()%50 - 25;
cout << a[j][k] << ‘\t‘;
}
cout << endl;
}
cout << endl;
MaxSum = a[0][0];
Maxd1 = a[0][0];
for (int i = 0;i < E;i++)
{
for (int i1 = 0;i1 < E-i;i1++)
{
for (int j = 0;j < F;j++)
{
line[j] = 0;
}
for (int i2 = i1;i2 <= i1+i;i2++)
{
for (int j = 0;j < F;j++)
{
line[j] += a[i2][j];
}
}
sum = 0;
for (int k = 0;k < F;k++)
{
sum += line[k];
if (sum > MaxSum)
{
MaxSum = sum;
end1[i][i1] = k;
i_max = i;
j_max = i1;
}
if(sum < 0)
{
sum = 0;
}
}
for (int k = F-1;k >= 0;k--)
{
d1 += line[k];
if (d1 > Maxd1)
{
Maxd1 = d1;
end2[i][i1] = k;
}
if(d1 < 0)
{
d1 = 0;
}
}
}
}
cout << "最大子数组为:" << endl;
for (int k = 0;k <= i_max;k++)
{
for (int k1 = end2[i_max][j_max];k1 <= end1[i_max][j_max];k1++)
{
cout << a[j_max+k][k1] << ‘\t‘;
}
cout << endl;
}
cout << endl;
cout << "最大子数组的和为: " << MaxSum << endl;
}
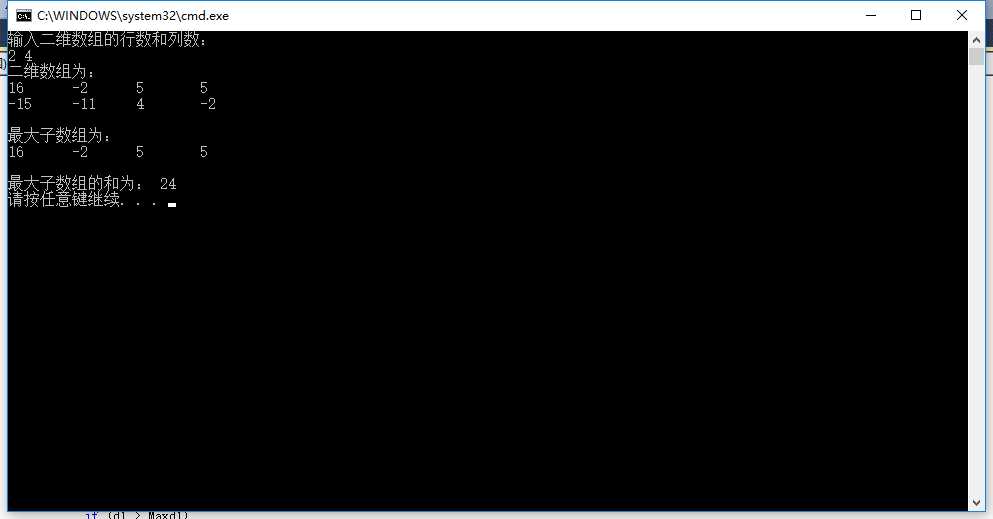
结果:
照片:
返回一个二维整数数组中最大子数组的和
标签:技术分享 sig 通过 char* str 探讨 连续 入口 应用
原文地址:https://www.cnblogs.com/lwan/p/9824755.html