标签:.com 一个 strong [] 9.png 实现 速度 长度 算法
复杂度也称为渐进复杂度,包括渐进时间复杂度和渐进空间复杂度,描述算法随数据规模变化而逐渐变化的趋势。复杂度分析是评估算法好坏的基础理论方法,所以掌握好复杂度分析方法是很有必要的。
首先,学习数据结构是为了解决“快”和“省”的问题,那么如何去评估算法的速度快和省空间呢?这就需要掌握时间和空间复杂度分析。同一段代码运行在不同环境、不同配置机器、处理不同量级数据…效率肯定不会相同。时间复杂度和空间复杂度是不运行代码,从理论上粗略估计算法执行效率的方法。时间复杂度一般用O来表示,如下例子:计算1,2,3…n的和。CPU执行每行代码时间很快,假设每行执行时间都一样为unit_time,第2行为一个unit_time,第3、4行都执行了n遍,那么下面这段代码执行的耗时时间可以这么计算:(1+2*n) * unit_time。
1 public int sum(int n) {
2 int sum = 0;
3 for (int i = 1; i <= n; i++) {
4 sum = sum + i;
5 }
6 return sum;
7 }
类似的再看一个例子:
1 public int sum(int n) {
2 int sum = 0;
3 int i = 1;
4 int j;
5 for (; i <= n; i++) {
6 j = 1;
7 for (; j <= n; j++) {
8 sum = sum + i * j;
9 }
10 }
11 return sum;
12 }
第2、3、4行分别执行执行了一次,时间为3unit_time,第5、6两行循环了n次为2n * unit_time,第7、8两行执行了n*n次为(n²) * unit_time,所以总的执行时间为:(2n²+2n+3) * unit_time
可以看出来,所有代码执行时间T(n)与每行代码执行次数成正比。可以用如下公式来表示:
T(n) = O(f(n))
T(n)表示代码的执行时间;
n表示数据规模大小;
f(n)表示每行代码执行的次数和,是一个表达式;
O表示执行时间T(n)和f(n)表达式成正比
那么上面两个时间复杂度可以表示为:
T(n) = O(1+2*n) 和 T(n) = O(2n²+2n+3)
实际上O并不表示具体的执行时间,只是表示代码执行时间随数据规模变化的趋势,所以时间复杂度实际上是渐进时间复杂度的简称。当n很大时,系数对结果的影响很小可以忽略,上面两个例子的时间复杂度可以粗略简化为:
T(n) = O(n) 和 T(n) = O(n²)
因为时间复杂度是表示的一种趋势,所以常常忽略常量、低阶、系数,只需要最大阶量级就可以了。
上面例子可以看出,复杂度忽略了低阶、常量和系数,所以执行最多的那一段最能表达时间复杂度的趋势。
还是上面的例子,总的时间复杂度等于各部分代码时间复杂度的和,求和之后再用最能表达趋势的项来表示整段代码的时间复杂度。
上面第二段代码,j 循环段嵌套在 i 循环内部,所以 j 循环体内的时间复杂度等于单独 i 的时间复杂度乘以单独 j 的时间复杂度。
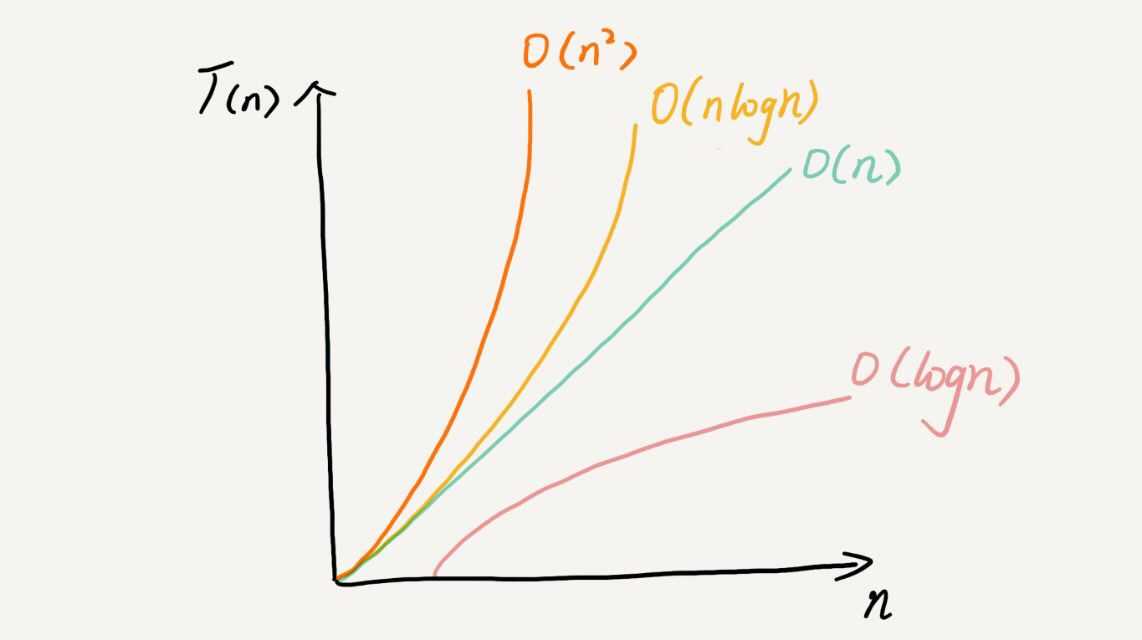
常见的复杂度有以下几种
可以这么来理解:如果一段代码有1000或10000行甚至更多,行数是一个常量,不会随着数据规模增大而变化,我们就认为时间复杂度为一个常量,用O(1)表示。
这几种复杂度效率曲线比较
模拟一个数组动态扩容例子,如果数组长度够,直接往里面插入一条数据;反之,将数组扩充一倍,然后往里面插入一条数据:
1 int[] arr = new int[10]; 2 int len = arr.length; 3 int i = 0; 4 public void add(int item) { 5 if (i >= len) { 6 int[] new_arr = new int[len * 2]; 7 for (int i = 0; i < len; i++) { 8 new_arr[i] = arr[i]; 9 } 10 arr = new_arr; 11 len = arr.length; 12 } 13 arr[i] = item; 14 i++; 15 }
最好情况下某个算法的时间复杂度。最好情况下,数组空间足够,只需要执行插入数据就可以了,此时时间复杂度是O(1)。
最坏情况下某个算法的时间复杂度。最坏情况下数组满了,需要先申请一个空间为原来两倍的数组,然后将数据拷贝进去,此时时间复杂度为O(n)。一般情况下我们说算法复杂度就是指的最坏情况时间复杂度,因为算法时间复杂度不会比最坏情况复杂度更差了。
最好时间复杂度和最坏时间复杂度都是极端情况下的时间复杂度,发生的概率并不算很大。平均时间复杂度是描述各种情况下平均的时间复杂度。上面的动态扩容例子将1到n+1次为一组来分析,前面n次的时间复杂度都是1,第n+1次时间复杂度是n,将一个数插入数组里的1 至 (n+1)个位置概率都为1/(n+1),所以平均时间复杂度为:
O(n) = (1 + 1 + 1 + …+n)/(n+1) = O(1)
对一个数据结构进行一组连续的操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连续的关系。并且和这组数据类型的情况循环往复出现,这时候可以将这一组数据作为一个整体来分析,看看是否可以将最后一个耗时的操作复杂度均摊到其他的操作上,如果可以,那么这种分析方法就是均摊时间复杂度分析法。上面的例子来讲,第n+1次插入数据时候,数组刚好发生扩容,时间复杂度为O(n),前面n次刚好将数组填满,每次时间复杂度都为O(1),此时可以将第n+1次均摊到前面的n次上去,所以总的均摊时间复杂度还是O(1)。
类比时间复杂度,如下代码所示,第2行申请了一个长度为n的数据,第三行申请一个变量i为常量可以忽略,所以空间复杂度为O(n)
1 public void init(int n) { 2 int[] arr = new int[n]; 3 int i = 0; 4 for (; i < n; i++) { 5 arr[i] = i + 1; 6 } 7 }
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元,若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为O(1)。
标签:.com 一个 strong [] 9.png 实现 速度 长度 算法
原文地址:https://www.cnblogs.com/mr-yang-localhost/p/9863168.html