标签:数组 number nbsp san bool pack hang exit rand
1. 前提
2. 优化策略1:主元(Pivot)的选取
归并排序(Merge Sort)有一个很大的优势,就是每一次的递归都能够将数组平均二分,从而大大减少了总递归的次数。
而快速排序(Quick Sort)在这一点上就做的很不好。
快速排序是通过选择一个主元,将整个数组划分(Partition)成两个部分,小于等于主元 and 大于等于主元。
这个过程对于数组的划分完全就是随机的,俗称看脸吃饭。
这个划分是越接近平均二分,那么这个划分就越是优秀;而若果不巧取到了数组的最大值或是最小值,那这次划分其实和没做没有什么区别。
因此,主元的选取,直接决定了一个快速排序的效率。
通过之前快速排序的学习,我们知道了基本上有两种主流的划分方式,我将其称之为:
前者将最左侧的数作为主元,后者将最右侧的数作为主元,这种行为完全就是随机取数。
最简单的的方法,就是在范围内取一个随机数,但是这种方法从概率的角度上来说,和之前的没有区别。
进一步的思考,可以从范围内随机取出三个数字,找到三个数字的中位数,然后和原主元的位置进行交换。
将中位数作为主元,相比于随机取出的另外两个数字,对于划分的影响还是很明显的。
1 package com.gerrard.sort.compare.quick.partition.pivot; 2 3 import com.gerrard.util.RandomHelper; 4 5 public final class MediumPivot implements Pivot { 6 7 @Override 8 public int getPivotIndex(int[] array, int left, int right) { 9 int index1 = RandomHelper.randomBetween(left, right); 10 int index2 = RandomHelper.randomBetween(left, right); 11 int index3 = RandomHelper.randomBetween(left, right); 12 if (array[index1] > array[index2]) { 13 if (array[index2] > array[index3]) { 14 return index2; 15 } else { 16 return array[index1] > array[index3] ? index3 : index1; 17 } 18 } else { 19 if (array[index1] > array[index3]) { 20 return index3; 21 } else { 22 return array[index2] > array[index3] ? index3 : index2; 23 } 24 } 25 } 26 }
3. 优化策略2:阈值的选取
同样是参考归并排序的优化策略,归并排序可以通过判断数组的长度,设定一个阈值。
数组长度大于阈值的,使用归并排序策略。
数组长度小于阈值的,使用直接插入排序。
通过这种方式,归并排序避免了针对小数组时候的递归(递归层次增加最多的场景,就是大量的小数组),从而减轻了JVM的负担。
1 public class OptimizedQuickSort implements Sort { 2 3 private ThreeWayPartition partitionSolution = new ThreeWayPartition(); 4 private int threshold = 2 << 4; 5 6 public void setPartitionSolution(ThreeWayPartition partitionSolution) { 7 this.partitionSolution = partitionSolution; 8 } 9 10 public void setThreshold(int threshold) { 11 this.threshold = threshold; 12 } 13 14 @Override 15 public void sort(int[] array) { 16 sort(array, 0, array.length - 1); 17 } 18 19 private void sort(int[] array, int left, int right) { 20 if (right - left < threshold) { 21 insertionSort(array, left, right); 22 } else if (left < right) { 23 int[] partitions = partitionSolution.partition(array, left, right); 24 sort(array, left, partitions[0] - 1); 25 sort(array, partitions[1] + 1, right); 26 } 27 } 28 29 private void insertionSort(int[] array, int startIndex, int endIndex) { 30 for (int i = startIndex + 1; i <= endIndex; ++i) { 31 int cur = array[i]; 32 boolean flag = false; 33 for (int j = i - 1; j > -1; --j) { 34 if (cur < array[j]) { 35 array[j + 1] = array[j]; 36 } else { 37 array[j + 1] = cur; 38 flag = true; 39 break; 40 } 41 } 42 if (!flag) { 43 array[0] = cur; 44 } 45 } 46 } 47 }
4. 优化策略3:三路划分
从上面的代码中,我们可以看到一个 ThreeWayPartition,这就是现在要讲的三路划分。
回顾之前的快速排序划分的描述:
快速排序是通过选择一个主元,将整个数组划分成两个部分,小于等于主元 and 大于等于主元。
不难发现,一次划分之后,我们将原数组划分成了三个部分,小于等于主元 and 主元 and 大于等于主元,划分结束之后,再将主元两侧进行递归。
由此可见,等于主元的部分被划分到了三个部分,那么我们就有了这样的思考:
能不能将数组明确地划分成三个部分:小于主元 and 主元和等于主元 and 大于主元。
这样一来,等于主元的部分就直接从下一次的递归中去除了。
回看一下 “挖坑取数” 的代码:
1 @Override 2 public int partition(int[] array, int left, int right) { 3 int pivot = array[left]; 4 int i = left; 5 int j = right + 1; 6 boolean forward = false; 7 while (i < j) { 8 while (forward && array[++i] <= pivot && i < j) ; 9 while (!forward && array[--j] >= pivot && i < j) ; 10 ArrayHelper.swap(array, i, j); 11 forward ^= true; 12 } 13 return j; 14 }
在内循环中,我们的判断条件是: array[++i] <= pivot。
在这个基础上,再做一次判断,针对等于 pivot 的情况,将等于 pivot 的值,与一个已经遍历过的位置交换:
那么,在整个划分结束之后,我们会得到这么一个数据模型:

其中:
然后将 left->p 的数据依次交换到 i 的左侧,同理,将q->right 的数据依次交换到 j 的右侧。
这样我们就能得到整个数组关于 pivot 的严格大小关系:
1 package com.gerrard.sort.compare.quick.partition; 2 3 import com.gerrard.sort.compare.quick.partition.pivot.Pivot; 4 import com.gerrard.util.ArrayHelper; 5 6 /** 7 * Three-Way-partition is an optimized solution for partition, also with complexity O(n). 8 * It directly separate the original array into three parts: smaller than pivot, equal to pivot, larger than pivot. 9 * It extends {@link SandwichPartition} solution. 10 * 11 * Step1: Select the left one as pivot. 12 * Step2: Besides i and j, define two more index p and q as two sides index. 13 * Step3: Work as SandwichPartition, from sides->middle, the only difference is: 14 * when meeting equal to pivot scenario, swap i and p or j and q. 15 * 16 * Step4: After iterator ends, the array should look like: 17 * 18 * left i=j right 19 * --------------------------------------------------- 20 * | | | | | | | 21 * --------------------------------------------------- 22 * p p‘ q‘ q 23 * 24 * The distance between left->p and p‘->i should be same. 25 * The distance between j->q‘ and q->right should also be same. 26 * [left,p) and (q,right] is equal to pivot, [p,i) is smaller than pivot, (j,q] is larger than pivot. 27 * 28 * Step5: Exchange [left,p) and [p‘,i), exchange (q,right] and (j,q‘]. 29 * Step6: Returns two number p‘-1 and q‘+1. 30 * 31 */ 32 public final class ThreeWayPartition { 33 34 public int[] partition(int[] array, int left, int right) { 35 if (pivotSolution != null) { 36 int newPivot = pivotSolution.getPivotIndex(array, left, right); 37 ArrayHelper.swap(array, left, newPivot); 38 } 39 int pivot = array[left]; 40 int i = left; 41 int j = right + 1; 42 int p = i; 43 int q = j - 1; 44 boolean forward = false; 45 while (i < j) { 46 while (forward && array[++i] <= pivot && i < j) { 47 if (array[i] == pivot) { 48 ArrayHelper.swap(array, i, p++); 49 } 50 } 51 while (!forward && array[--j] >= pivot && i < j) { 52 if (array[j] == pivot) { 53 ArrayHelper.swap(array, j, q--); 54 } 55 } 56 ArrayHelper.swap(array, i, j); 57 forward ^= true; 58 } 59 while (p > left) { 60 ArrayHelper.swap(array, --p, --i); 61 } 62 while (q < right) { 63 ArrayHelper.swap(array, ++q, ++j); 64 } 65 return new int[]{i, j}; 66 } 67 }
5. 优化测试
最后,针对各种快速排序的算法,我做了一系列的性能测试:
1 package com.gerrard.helper; 2 3 import com.gerrard.sort.Sort; 4 5 public final class ComparableTestHelper { 6 7 private ComparableTestHelper() { 8 9 } 10 11 public static void printCompareResult(int[] array, Sort... sorts) { 12 for (Sort sort : sorts) { 13 int[] copyArray = ArrayTestHelper.copyArray(array); 14 long t1 = System.nanoTime(); 15 sort.sort(copyArray); 16 long t2 = System.nanoTime(); 17 double timeInSeconds = (t2 - t1) / Math.pow(10, 9); 18 System.out.println("Algorithm " + sort + ", using " + timeInSeconds + " seconds"); 19 } 20 } 21 }
测试结果:
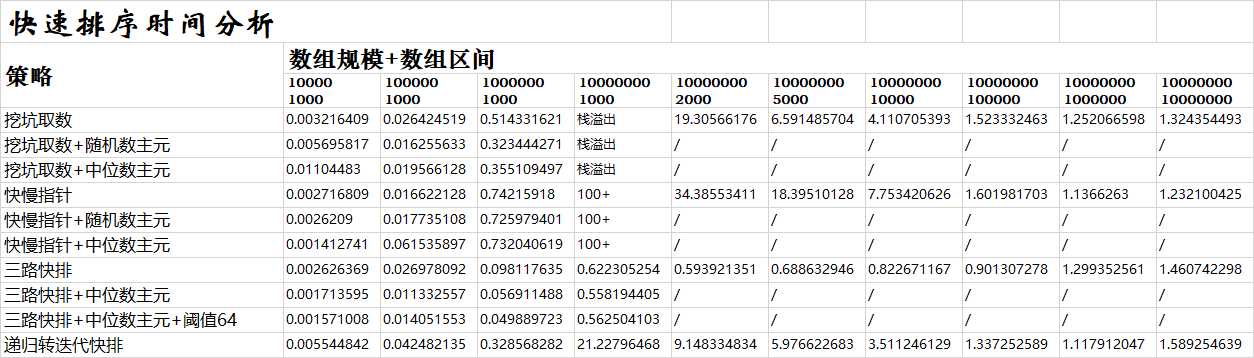
从测试结果中,我们可以发现:
但是还有几个比较奇怪的现象:
希望有读者能够解惑这些现象。
标签:数组 number nbsp san bool pack hang exit rand
原文地址:https://www.cnblogs.com/jing-an-feng-shao/p/9865644.html