1. 多层神经网络存在的问题  

  常用的神经网络模型, 一般只包含输入层, 输出层和一个隐藏层：

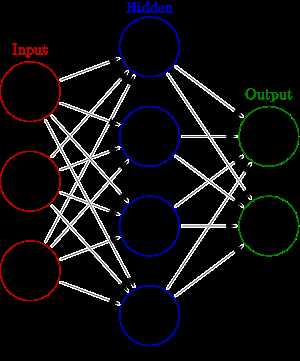
  理论上来说, 隐藏层越多, 模型的表达能力应该越强。但是, 当隐藏层数多于一层时, 如果我们使用随机值来初始化权重, 使用梯度下降来优化参数就会出现许多问题[1]:

1. 如果初始权重值设置的过大, 则训练过程中权重值会落入局部最小值(而不是全局最小值)。
2. 如果初始的权重值设置的过小, 则在使用BP调整参数时, 当误差传递到最前面几层时, 梯度值会很小, 从而使得权重的改变很小, 无法得到最优值。[疑问, 是否可以提高前几层的learning rate来解决这个问题?]

  所以, 如果初始的权重值已经比较接近最优解时, 使用梯度下降可以得到一个比较好的结果, Hinton等在2006年提出了一种新的方法[2]来求得这种比较接近最优解的初始权重。

2. Deep Belief Network

  DBN是由Hinton在2006年提出的一种概率生成模型, 由多个限制玻尔兹曼机(RBM)[3]堆栈而成:

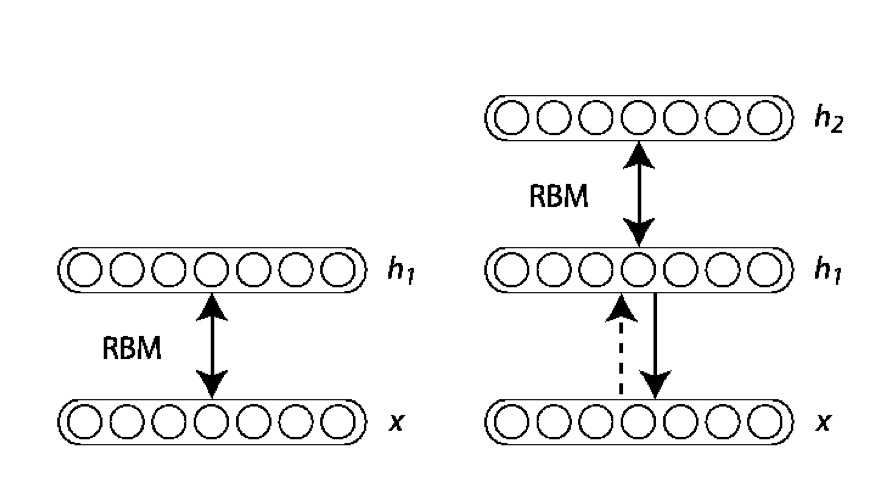
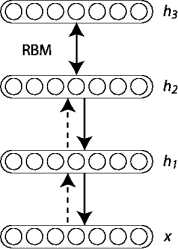
  在训练时, Hinton采用了逐层无监督的方法来学习参数。首先把数据向量x和第一层隐藏层作为一个RBM, 训练出这个RBM的参数(连接x和h₁的权重, x和h₁各个节点的偏置等等), 然后固定这个RBM的参数, 把h₁视作可见向量, 把h₂视作隐藏向量, 训练第二个RBM, 得到其参数, 然后固定这些参数, 训练h₂和h₃构成的RBM, 具体的训练算法如下:

  上图最右边就是最终训练得到的生成模型:

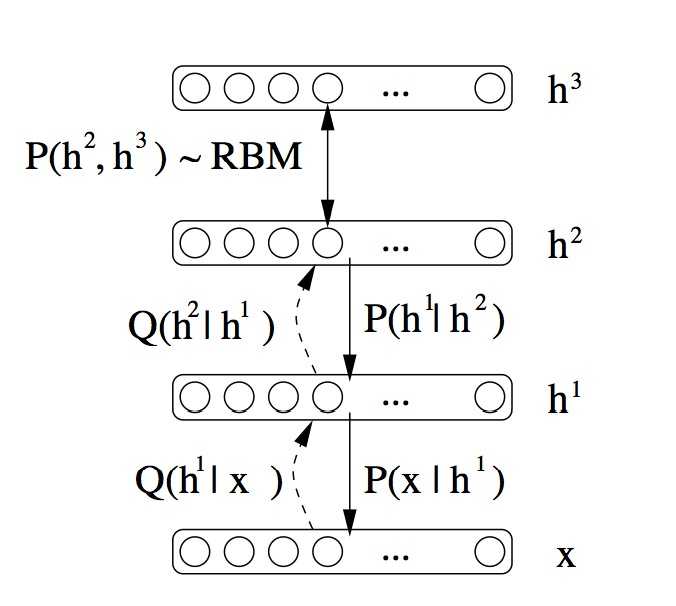
  用公式表示为:

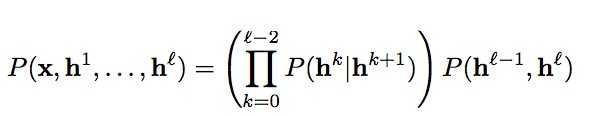
3. 利用DBN进行有监督学习

  在使用上述的逐层无监督方法学得节点之间的权重以及节点的偏置之后(亦即初始化), 可以在DBN的最顶层再加一层, 来表示我们希望得到的输出, 然后计算模型得到的输出和希望得到的输出之间的误差, 利用后向反馈的方法来进一步优化之前设置的初始权重。因为我们已经使用逐层无监督方法来初始化了权重值, 使其比较接近最优值, 解决了之前多层神经网络训练时存在的问题, 能够得到很好的效果。

  参考文献:

  [1]. Reducing the Dimensionality of Data with Neural Networks. G. E. Hinton, R. R. Slakhutdinov. 2006, Science.

  [2]. A fast learning algorithm for deep belief nets. G. E. Hinton, Simon Osindero, Yee-Whye Teh. 2006, Neural Computation.

  [3]. 限制玻尔兹曼机(Restricted Boltzmann Machine, RBM)简介

  [4]. Scholarpedia: Deep Belief Networks

  [5]. Learning Deep Architectures for AI. Yoshua Bengio