【Delphi】如何在三轴加速器的频谱分析中使用FFT(快速傅里叶变换)算法

标签：cdc   lib   高通   中间   glib   ima   采集   abs   机器学习   

       关于傅里叶变换的作用，网上说的太过学术化，且都在说原理，已经如何编码实现，可能很多人有个模糊影响，在人工智能，图像识别，运动分析，机器学习等中，频谱分析成为了必备的手段，可将离散信号量转换为数字信息进行归类分析。

今天这里将的不是如何实现，而是如何使用傅里叶变换

       但频谱分析中，涉及到的信号处理知识对大部分软件开发的人来说，太过于晦涩难懂，傅里叶变换，拉普拉斯，卷积，模相，实数，虚数，复数，三角函数等等，已经能让软件工程师望而却步，造成懂知识的人无法开发，懂开发的人无法分析，而同时具备两种技能的人，除了专业的研究生博士，剩下的少之又少。

       站在软件开发人员的角度，能否抛开这些晦涩难懂概念，进行纯软件方面的信号处理？这个问题可能没有答案，最好能够通过实践来证明。而且若是抛开这些概念，让那些有兴趣的开发人员学习到信号处理，频谱分析，先不管可不可能，光想想，其作用也是有的，至少“高深”的东西能够被用上了。

三轴加速器步数计算分析

       下面就以三轴加速器的实际应用开发为例，来讲一讲（限于个人水平，可能比较粗略）。

       试下运动APP也有不少，不少APP开发人员就会接触到陀螺仪，加速器等，利用这些传感器进行行为分析，首先需要获取传感器的数据，将获取的数据输出到平面坐标图表中：

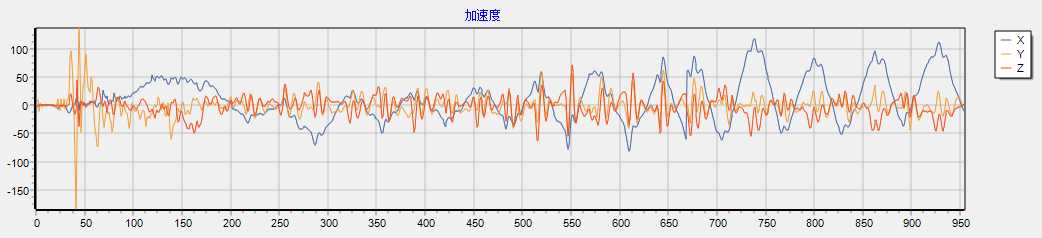
       在上图中，采集频率为50Hz，即X轴每一个点为50分之1秒，可以看到前4秒（0-200）没有太明显走动，4秒后到12秒走动速度较慢，12秒走路稍微加快。在这里不得不感叹人脑简直是宇宙超级无敌，光看图表就能够直接知道行为，无法想象未来谁能够让人工智能能够超越人脑。

        在软件开发中，我们要如何通过代码分析得到上面“人脑的分析结果“？ 要直接上代码不是我的作风，百度可以搜到一篇腾讯的文章《利用三轴加速器的计步测算方法》，此文章的分析方法可以说大致能够理解，涉及到的计算方法却语焉不详，比如，在没有进行滤波前，上图的X轴波峰波谷并不平滑，可以看出每个大波峰上又有2个小波谷，如果以此来计算，得出来的步数误差非常大。

        可能一些做过信号处理的人会说，做一个均值滚动滤波+低通滤波+高通滤波就差不多了，我只能说对于复杂的周期性信号分析是可行的，对于三轴加速器的步数计算来说，实际中并不存在什么周期性信号，人的上坡下坡走路非直线，时快时慢等动作都会加大分析难度。

        先不说这么多了，拿到信号原始数据，马上进行傅里叶变换，Delphi可以使用FPC一个开源的库AlgLib，最新版好像不开源了且分为免费版和收费版，但codetyphon收录了以前的开源版本可以用。

        alglib中关于快速傅里叶变换是在u_fft.pp文件中，delphi只把后缀pp改成pas就可以使用了。使用FFTC1D函数进行变换，其中N即为采集的数据量，当然实际中我们有时候采集了几十秒，而N的最佳范围是在128-2048范围（既充分又计算量不高），所以我们每10秒（50Hz即500个数据）进行一次傅里叶变换分析即可。

FFTC1D函数函数的调用方法

        比如采集到的数据为[3.4,  4.1, 6.7, 3.1...],则如下代码：

var 
  A : TComplex1DArray; 
  I, N : Integer;
begin
   N := 50*10 // 10秒
   SetLength(A, N);
   for I:=0 to N-1 do
   begin
      A[I].X:=I;  //即时域的刻度
      A[I].Y:=Data[nIdx]; //填上采集的数据
   end;
   FFTC1D(A);

   //////////////////////////
   // 到这里已经完成傅里叶变换，如何使用变换后的数据？？  
end;

这里先引用百科上的一段话来帮助理解下面代码：

假设FFT之后某点n用复数a+bi表示，
那么这个复数的模就是An=根号a*a+b*b，
相位就是Pn=atan2(b,a)。
根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：An/(N/2)*cos(2*pi*Fn*t+Pn)，即2*An/N*cos(2*pi*Fn*t+Pn)。
对于n=1点的信号，是直流分量，幅度即为A1/N。

由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。

       经过变换后的复数数组A，即是变换结果，但并不是分析的数据，而是一个中间数据，由该数据可以得到模值和相位，根据傅里叶变换原理，模值计算如下：

// 对A数组每个点的复数求模，即实部和虚部平方和再开根号。 
nAValue := Math.Power(Abs(A[I].X*A[I].X)+Abs(A[I].Y*A[I].Y), 0.5); 

　　至于相位则是根据公式Pn=atan2(b,a)计算，但是频谱分析比较有用的是模值（主要是滤波），所以其他不管，当然幅度也有一定作用。

       前面讲到使用10秒的数据进行计算，这样得到的傅里叶变换结果复数也有500个，由于傅里叶的对称性，我们只取0-250的结果来计算模值即可，因为251-500是对称的结果。

       计算模值后再输出平面坐标图表，如下：

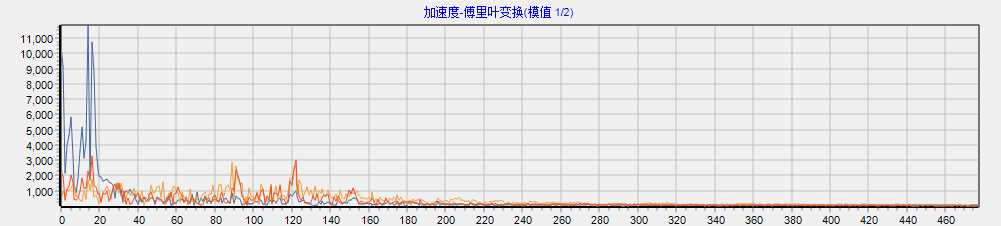
如上图，各种傅里叶变换文章中的结果图就出来了（请忽略图中的时间刻度与文章的10秒500个数据等相关性，因为我用的图是随便一段数据来的。）

看到上面的傅里叶变换结果图，会不会觉得悲剧才开始发生。没错，结果是出来了，但我们该如何分析呢？

如何分析傅里叶变换结果

【Delphi】如何在三轴加速器的频谱分析中使用FFT(快速傅里叶变换)算法

标签：cdc   lib   高通   中间   glib   ima   采集   abs   机器学习   

原文地址：https://www.cnblogs.com/caibirdy1985/p/9896617.html