标签：ali   一个   情况下   性能   就会   遇到   插入   extends   tab   

2018-2019-20172321 《Java软件结构与数据结构》第七周学习总结

教材学习内容总结

第11章 二叉查找树

一、概述

• 二叉查找树是一种含有附加属性的二叉树，该属性即其左孩子小于父节点，而父节点又小于等于其右孩子。如下图所示。根结点的左子树每个元素都小于80，右子树每个元素都大于80.

• 查找方法，要判定一个具体的目标是否存在于树中，需要沿着从根开始的路径，根据查找目标是小于还是大于当前结点的值，相应地转到当前结点的左子结点或右结点。最终或是找到目标元素，或是遇到路径的末端，后者意味着目标不在树中。

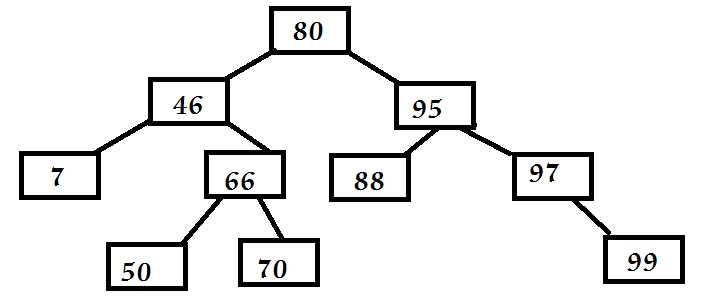
• 在二叉查找树中添加元素，改过程类似于树的查找过程，新元素添加为树的叶结点，从根开始，沿着每个结点中元素所确定的路径，直到相应地方向上没有子结点为止，此时，将新元素添加为叶结点。

  如果没有其他操作，二叉查找树的树形由元素的添加顺序来决定。

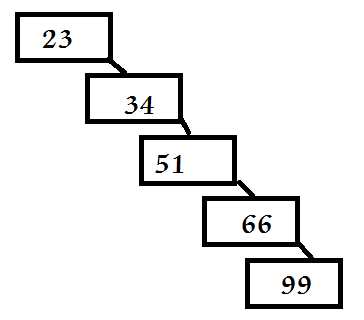
• 注:如果输入是完全有序的，二叉查找树就会退化为一个有序链表，削弱了它本身的价值，如下图所示。

• 在二叉查找树中删除元素，要考虑如下三种情况（参考下图）：

• 第一种情况：如果被删除的结点是叶结点（无子结点），可以简单地删除
• 第二种情况：如果被删除的结点是只有一个子结点，则用它的子结点替代它

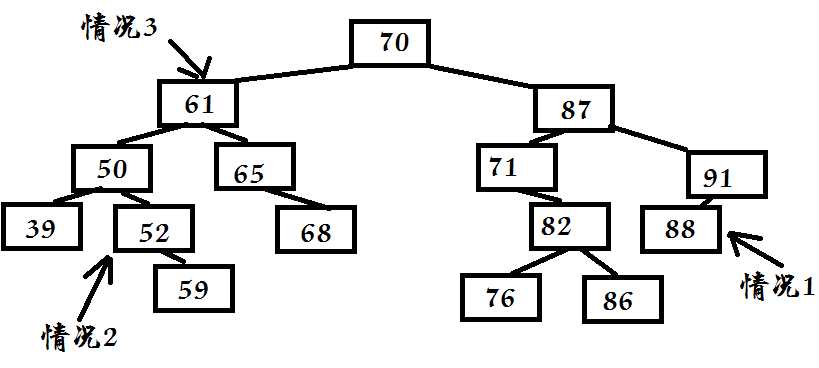
• 第三种情况，如果被删除结点有两个子结点，在树的更低层找到一个合适的结点来代替它。被删除结点的子结点成为替代结点的子结点。

  当从二叉查找树中删除有两个子结点的结点是，比较好的办法是用它的中序后继来取代它，即在中序遍历中排在被删元素之后的那个元素（紧邻的下一个值）

• 二叉查找树的接口类继承自二叉树的接口类BinaryTreeADT

public interface BinarySearchTreeADT<T> extends BinaryTreeADT<T>
{
    public void addElement(T element);
    //往树中添加一个元素
    public T removeElement(T targetElement);
    // 从树中删除一个元素
    public void removeAllOccurrences(T targetElement);
    // 从树中删除所指定元素的任何存在
    public T removeMin();
    //删除树中最小元素
    public T removeMax();
    // 删除树中最大元素
    public T findMin();
    //返回一个指向树中最小元素的引用
    public T findMax();
    //返回一个指向树中最大元素的引用
}

二、平衡二叉查找树

• 在平衡二叉树中进行查找，比在退化的树中进行查找的效率高很多。在有n个结点的平衡树中进行查找及添加操作的效率是进行O(log2 n)次比较（最长路径的长度）。树越退化，查找及添加操作的时间复杂度越接近O(n)，它抵消了使用查找树带来的益处。

  可以对二叉查找树进行旋转以恢复平衡

• 右旋转

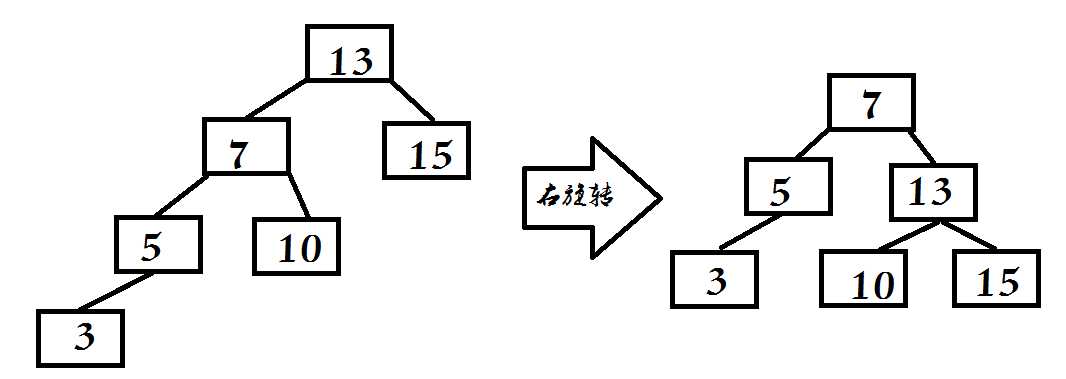
 1.令根的左子结点变为新的根
 2.令原根结点变为新的根结点的右子结点
 3.令原根的左子结点的右子结点变为原根结点的新的左子结点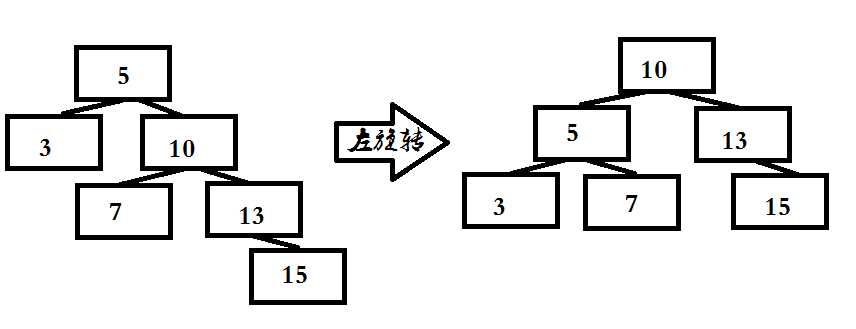

• 左旋转

 1.令根的右子结点变为新的根
 2.令原根结点变为新的根结点的左子结点
 3.令原根的右子结点的左子结点变为原根结点的新的右子结点

并非所有的不平衡情况都可以用一个单一的旋转解决，如果不平衡性是由根的右子结点的左子树的长路径引发的，则必须先绕那个异常子树执行一次右旋转，然后再绕根执行一次左旋转（右-左旋转）。如果不平衡是由根的左子结点的右子树中的长路径引发，则执行（左-右旋转）

三、AVL树

• AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。

四、红黑树

- 红黑树（RBT）是具有以下性质的二叉查找树：
- 1.节点非红即黑。
- 2.根节点是黑色。
- 3.所有NULL结点称为叶子节点，且认为颜色为黑。
- 4.所有红节点的子节点都为黑色。
- 5.从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

显然红黑树的平衡性能比AVL的略差些，但是经过大量试验证明，实际上红黑树的效率还是很不错了，仍能达到O(logN)

教材学习中的问题和解决过程

• 问题1：

代码调试中的问题和解决过程

代码托管

上周考试错题总结

没有测试

结对及互评

学习进度条

参考资料

• 《Java软件结构与数据结构》第四版
• 完全树-学术百科-知网空间
• 完美二叉树, 完全二叉树和完满二叉树

2018-2019-20172321 《Java软件结构与数据结构》第七周学习总结

标签：ali   一个   情况下   性能   就会   遇到   插入   extends   tab   

原文地址：https://www.cnblogs.com/N-idhogg/p/9894910.html