标签：红色   必须   add   树的高度   开始   cti   contain   ceo   查找   

2018-2019-20172329 《Java软件结构与数据结构》第七周学习总结

教材学习内容总结

《Java软件结构与数据结构》第十一章-二叉查找树

一、概述

• 1、什么是二叉查找树：二叉查找树是一种带有附加属性的二叉树，即对树中的每个结点，其左孩子都要小于其父结点，而父结点又小于或等于其右孩子。

• 2、二叉查找树的定义是二叉树定义的扩展。

• 3、操作：

二、用链表实现二叉查找树

• 1、addElement操作

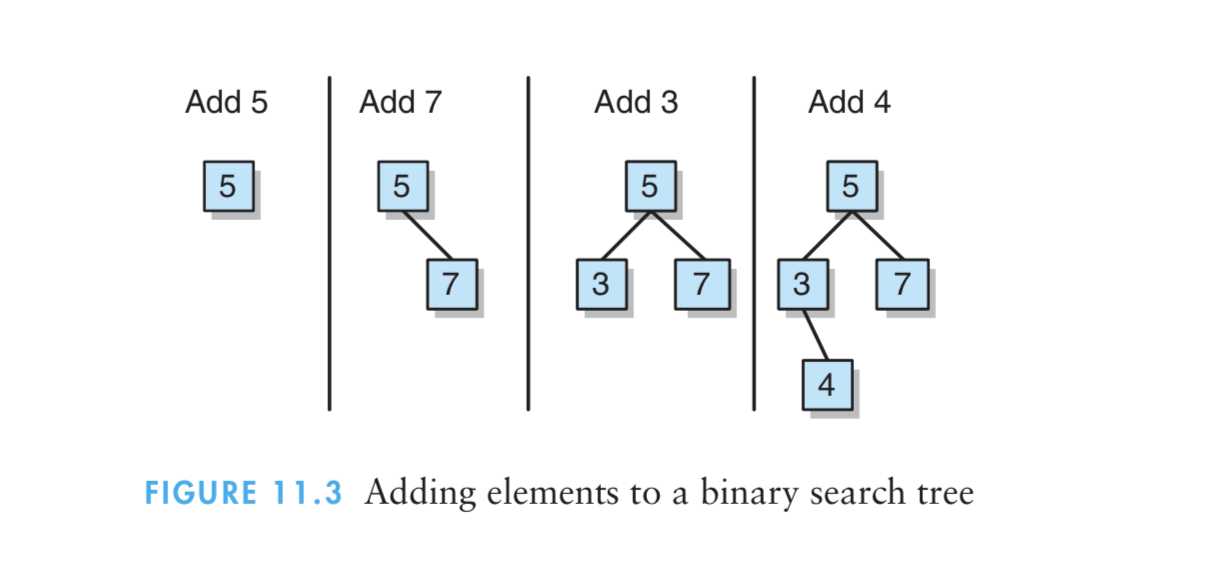
  • 过程：如果这个树为空，则新元素就将成为根结点。如果树非空，这个新元素会与树根元素进行对比。

    • （1）如果它小于根结点中存储的那个元素且根的左孩子为null，则这个新元素就将成为根的左孩子。

    • （2）如果这个新元素小于根结点中储存的那个元素且根的左孩子不是null，则会遍历根的左孩子，并再次进行比较操作。

    • （3）如果这个新元素大于或等于树根存储的那个元素且根的右孩子为null，则这个新元素会成为根的右孩子，并再次进行比较操作。

  • 图解：
    

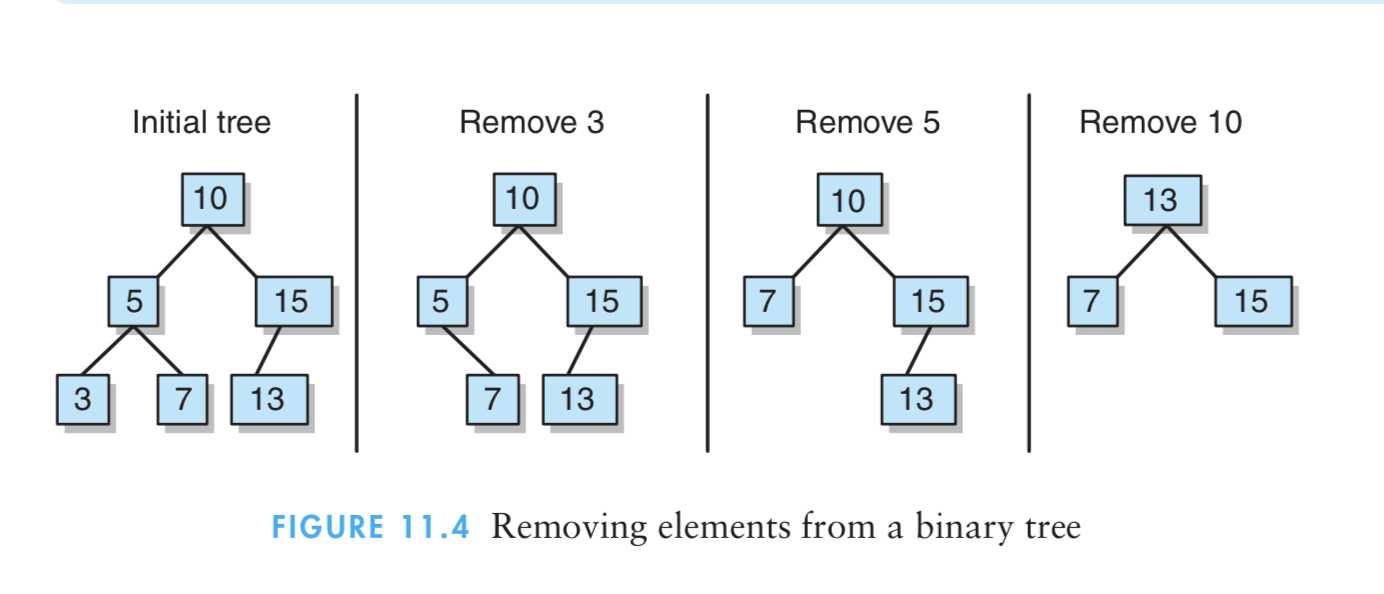
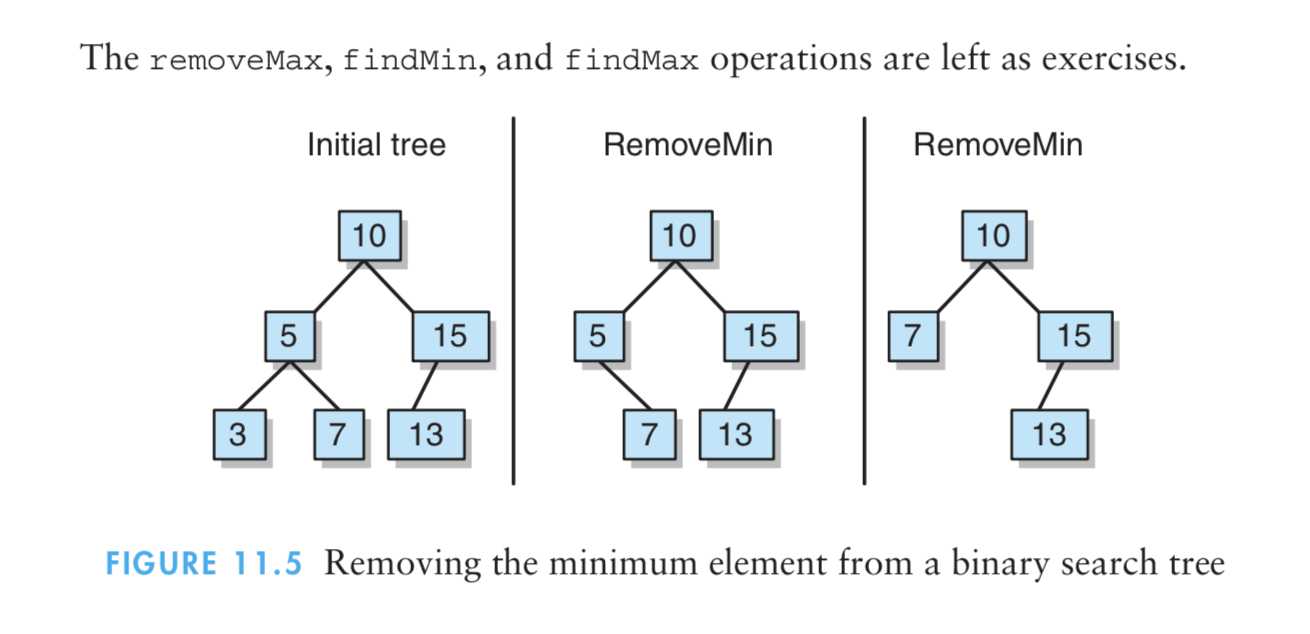
• 2、removeElement操作

  • 过程：

    • （1）如果被删除结点没有孩子，则replacement返回null。

    • （2）如果被删除结点只有一个结点，则replacement返回这个孩子。

    • （3）如果被删除结点有两个孩子，则replacement会返回中序后继者（因为相等元素会放到右边）

    • 注：从二叉查找树中删除一个元素时，必须推选出另一个结点来代替要被删除的那个结点。

  • 图解：
    

• 3、 removeMin操作
  • 过程：
    • （1）如果树根没有左孩子，则树根就是最小元素，而树根的右孩子会变成新的根结点。
    • （2）如果树的最左边结点是一片叶子，则这片叶子就是最小元素，这时只需设置其父结点的左孩子引用为null即可。
    • （3）如果树的最左侧结点是一个内部结点，则需要设置其父结点的左孩子引用指向这个将删除结点的右孩子。
    • 注：二叉查找树的最右侧结点会存放最大元素，而其最左侧结点会存放最小元素。
  • 图解：
    

三、用有序列表实现二叉查找树

• 1、BinarySearchTreeList实现的分析

注：*add操作和remove操作都可能导致树变的不平衡

四、平衡二叉树

• 1、下图显示了得到的二叉树，这个结果二叉树看作是一颗蜕化树，看起来更像是一个链表，而事实上，它的效率比链表还低。
  

• 2、如果没有平衡假设，最坏情况下addElement操作时间复杂性是O(n)而不是O(log n)，因为存在这种可能，即树根是书中的最小元素，而将被插入的元素可能是树中的最大元素。
• 3、如果二叉查找树不平衡，其效率可能比线性结构的还要低。
• 4、右旋
  • 用途：因为树根左孩子的左子树中较长的路径而导致的不平衡。
  • 步骤：
    • （1）使树根的左孩子元素成为新的根元素。
    • （2）使原根元素成为这个新树根的右孩子元素。
    • （3）使原树根的左孩子的右孩子，成为原树根的新的左孩子。
  • 图解：
    
• 5、左旋
  • 用途：由树根右孩子的右子树中较长的路径而导致的不平衡。
  • 步骤：
    • （1）使树根的右孩子元素成为新的根元素。
    • （2）使原根元素成为这个新树根的左孩子元素。
    • （3）使原树根右孩子结点的左孩子，成为原树根的新的右孩子。
  • 图解：
    
• 6、左右旋
  • 用途：对于由于树根左孩子的右子树中较长的路径而导致的不平衡，我们必须先让树根左孩子的右孩子绕着树根的左孩子进行一次左旋，然后再让所得的树根左孩子绕着树根进行一次右旋。
  • 图解：
    
• 7、右左旋
  • 用途：对于由树根右孩子的左子树中较长路径而导致的不平衡，我们必须先让树根右孩子的左孩子，绕着树根右孩子进行一次右旋，然后再让所得的树根右孩子绕着树根进行一次左旋。
  • 图解：
    

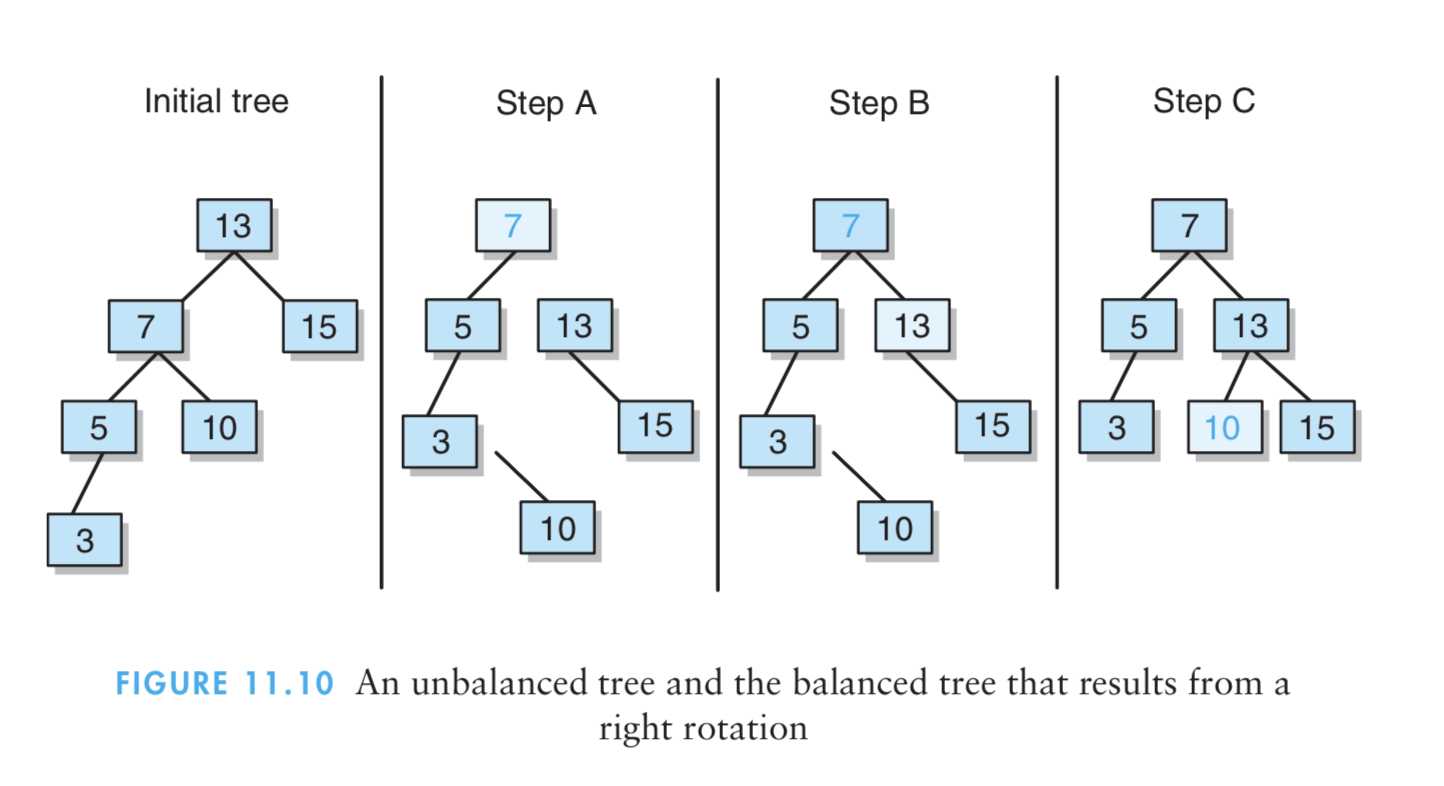
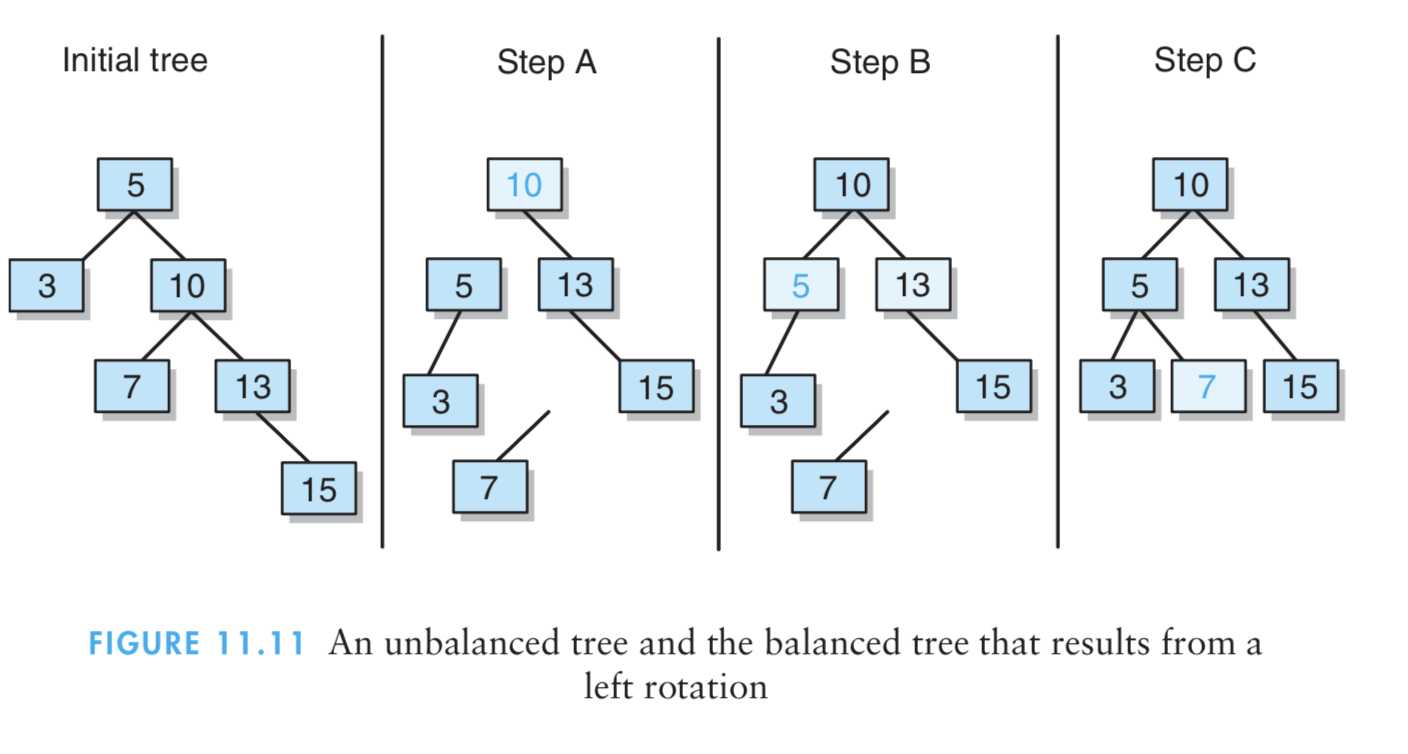
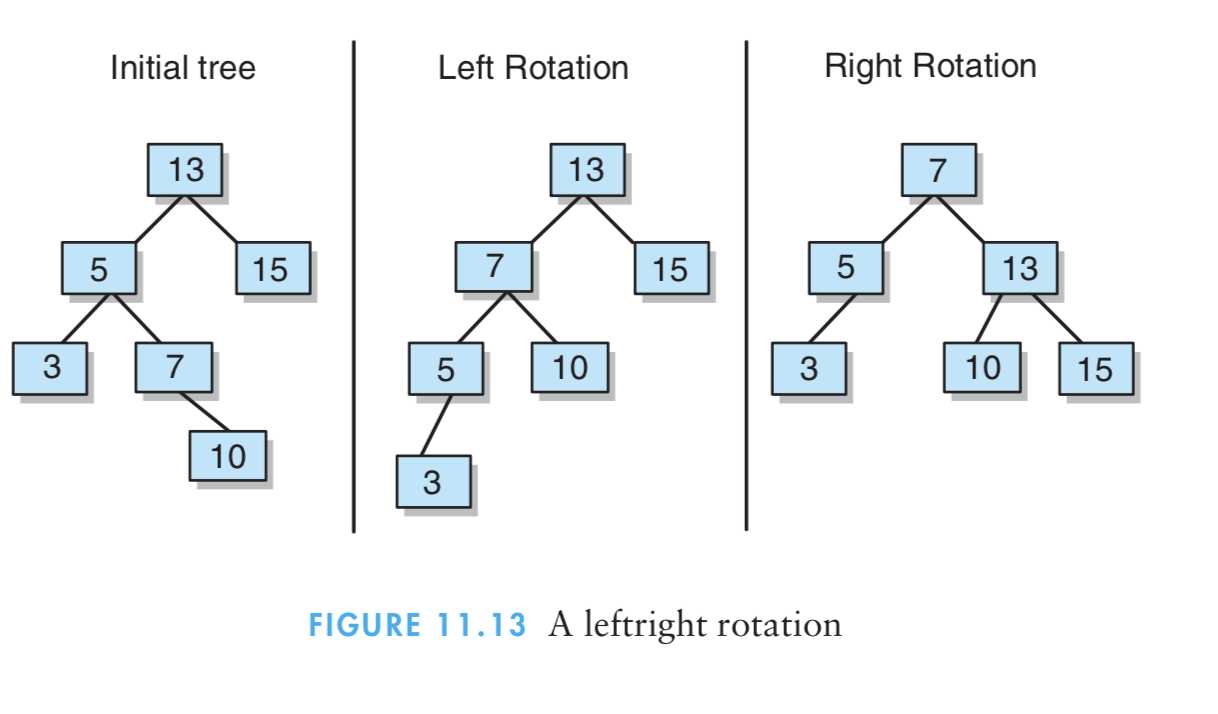
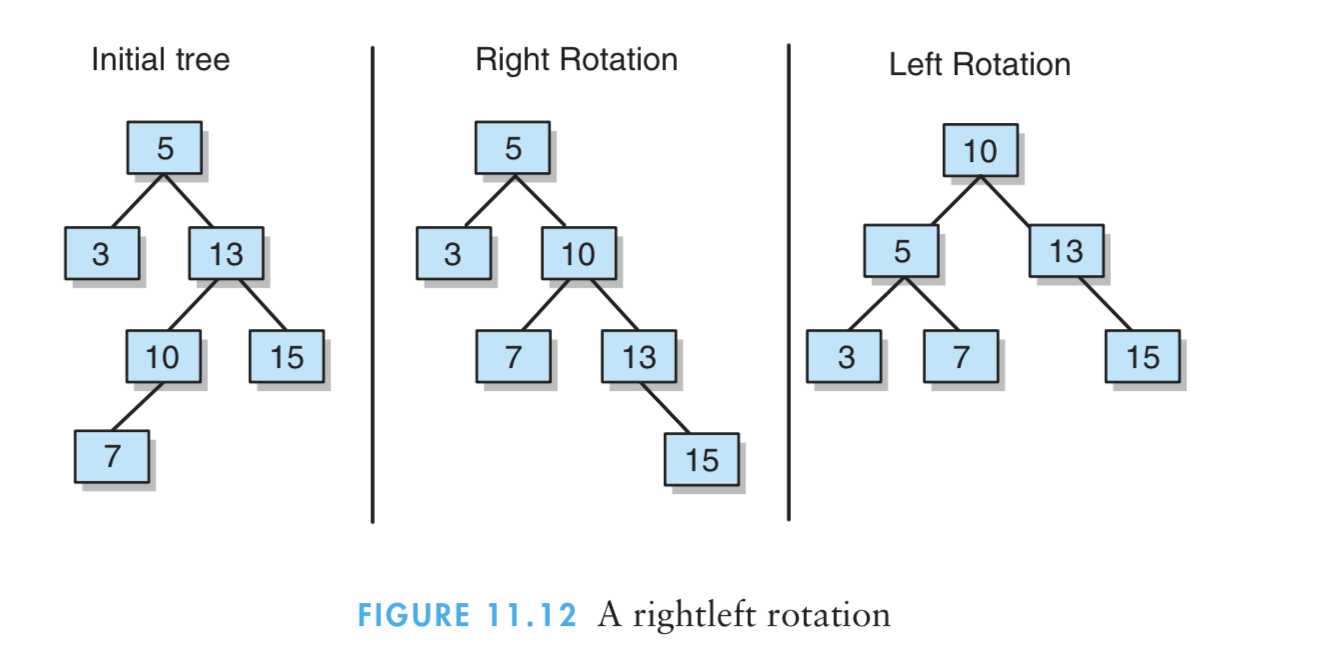
• 8、综上所述，平衡化树的一般性办法，其中自树根而下的路径最大长度必须不超过log2 n，而且自树根而下的路径最小长度必须不小于(log2 n)-1。
  五、实现二叉查找树：AVL树

• 1、什么是AVL树
  • 它是上述树的一种变体。对于树中的每个结点，我们都会跟踪起左右子树的高度。对于树中任何结点，如果其平衡因子（平衡因子指的是左右子树的高度差，即右子树的高度减去左子树的高度）大于1或小于-1，则以该结点为树根的子树需要重新平衡。
• 2、AVL树的操作（右旋，左旋，左右旋，右左旋）
  • 右旋：
    • 用在：平衡因子<-1且孩子的平衡因子<=-1
  • 左旋：
    • 用在：平衡因子>1且孩子的平衡因子>=1
  • 左右旋：
    • 用在：平衡因子<-1且孩子的平衡因子>=1
  • 右左旋：
    • 用在：平衡因子>1且孩子的平衡因子<=-1

• 删除结点的实例图：
  

• AVL树的性质：
  （1）左子树和右子树的高度之差的绝对值不超过1
  （2）树中的每个左子树和右子树都是AVL树
  （3）每个节点都有一个平衡因子(balance factor--bf),任一节点的平衡因子是-1,0,1之一
  六、实现二叉查找树：红黑树
• 1、什么是红黑树：红黑树是一种平衡二叉查找树，其中的每个结点存储一种颜色（黑色或者红色，通常用一个布尔值来实现，值false等价于红色）
• 2、规则：
  • （1）根结点为黑色。
  • （2）红色结点所有孩子都为黑色。
  • （3）从树根到树叶的每条路径都包含同样数目的黑色结点。
    

教材学习中的问题和解决过程

• 问题1：在书中225页中有一个类叫做超类，为什么叫做超类？
• 问题1解决方案：

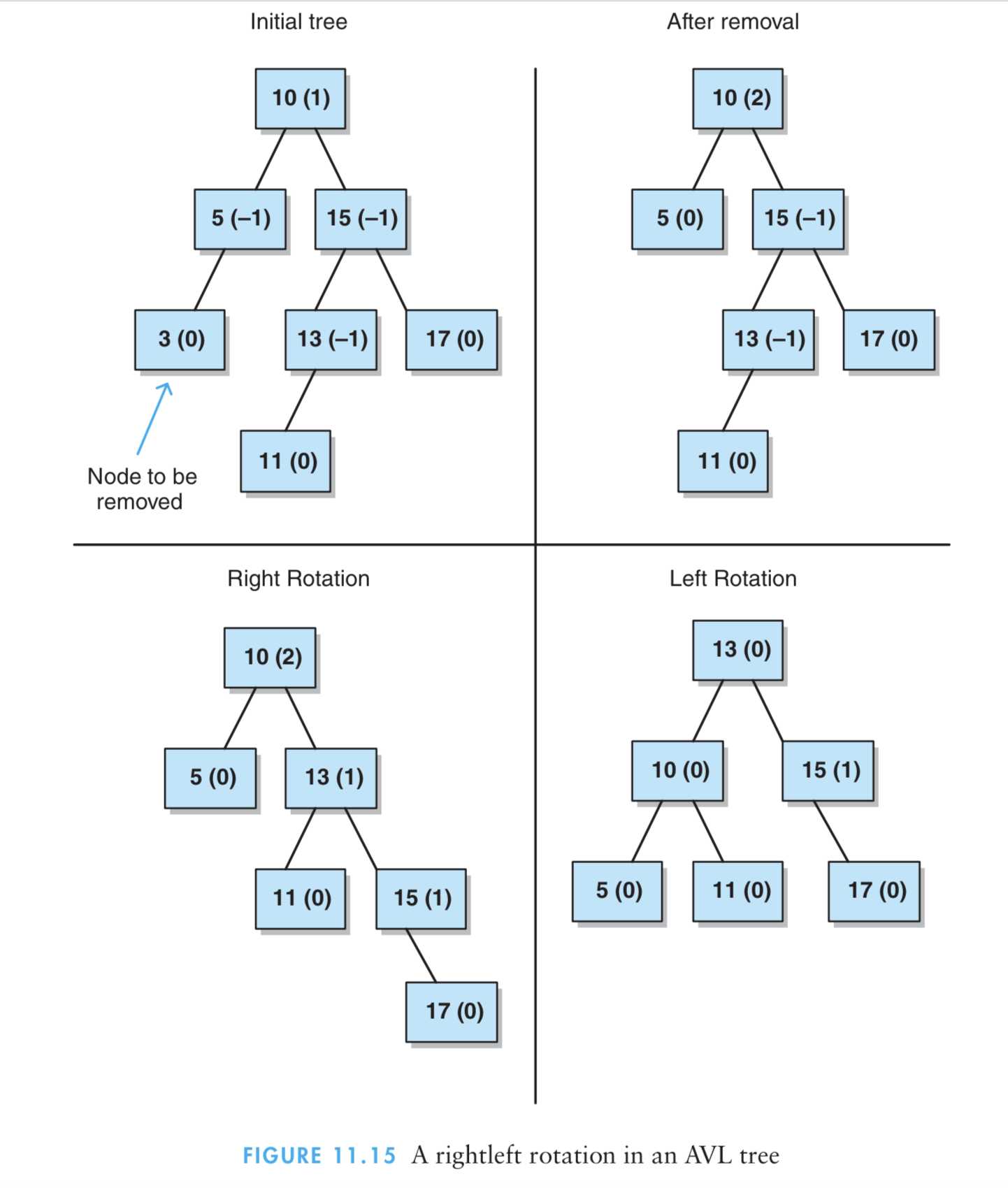
• 从网上查询了以后得知：
  是父类。
  超类(SuperClass) ：用java术语来讲,被继承的类称为超类(SuperClass)，也有叫做父类，继承的类称为子类。
  比如：
  public class A{//定义类A
  }
  public class B extends A{//定义类B，继承类A
  }
  则，类A就是超类或父类，类B叫子类

• 问题2：涉及红黑树的问题，对于我们大家都是一个难点，所以在教材问题中将红黑树具体来写一下：

• 问题2解决方案：
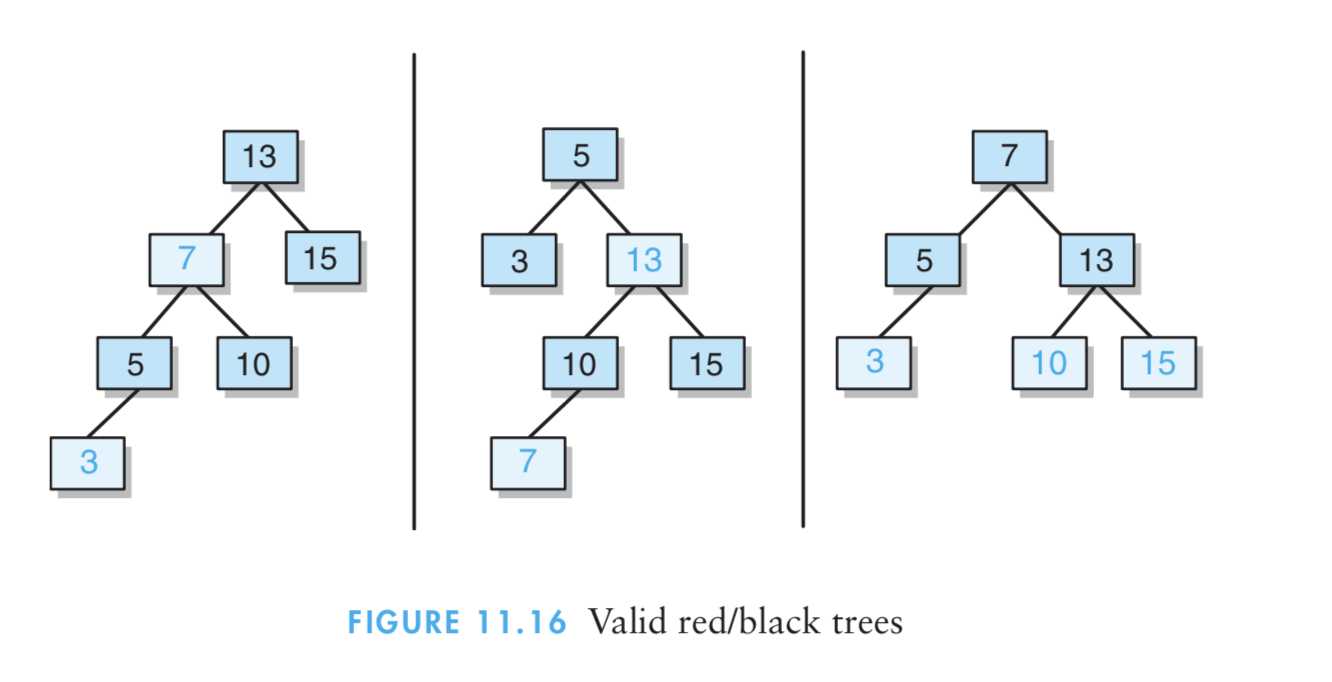
  （1）首先，我们需要了解到红黑树代表的是什么：红黑树是一种平衡二叉查找树，其中的每个结点存储一种颜色（红色或黑色，通常用一个布尔值来实现，值false等价于红色）。控制结点颜色的规则如下：

• 根结点为黑色。

• 红色结点的所有孩子都为黑色。

• 从树根到树叶的每条路径都包含同样数目的黑色结点。

（2）我们了解到在某种程度上，红黑树中的平衡限制没有AVL树那样的严格。但是，它们的序仍旧是log n。

（3）我们分析一下红黑树的时间复杂度：

• 红黑树的时间复杂度为: O(lgn)

• 下面通过“数学归纳法”对红黑树的时间复杂度进行证明。

• 定理：一棵含有n个节点的红黑树的高度至多为2log(n+1).

• 证明：
  "一棵含有n个节点的红黑树的高度至多为2log(n+1)" 的逆否命题是 "高度为h的红黑树，它的包含的内节点个数至少为 2h/2-1个"。

  我们只需要证明逆否命题，即可证明原命题为真；即只需证明 "高度为h的红黑树，它的包含的内节点个数至少为 2h/2-1个"。

  从某个节点x出发（不包括该节点）到达一个叶节点的任意一条路径上，黑色节点的个数称为该节点的黑高度(x‘s black height)，记为bh(x)。关于bh(x)有两点需要说明：
• 第1点：根据红黑树的"特性(5) ，即从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点"可知，从节点x出发到达的所有的叶节点具有相同数目的黑节点。这也就意味着，bh(x)的值是唯一的！

• 第2点：根据红黑色的"特性(4)，即如果一个节点是红色的，则它的子节点必须是黑色的"可知，从节点x出发达到叶节点"所经历的黑节点数目">= "所经历的红节点的数目"。假设x是根节点，则可以得出结论"bh(x) >= h/2"。进而，我们只需证明 "高度为h的红黑树，它的包含的黑节点个数至少为 2bh(x)-1个"即可。

  到这里，我们将需要证明的定理已经由
  "一棵含有n个节点的红黑树的高度至多为2log(n+1)"
  转变成只需要证明
  "高度为h的红黑树，它的包含的内节点个数至少为 2bh(x)-1个"

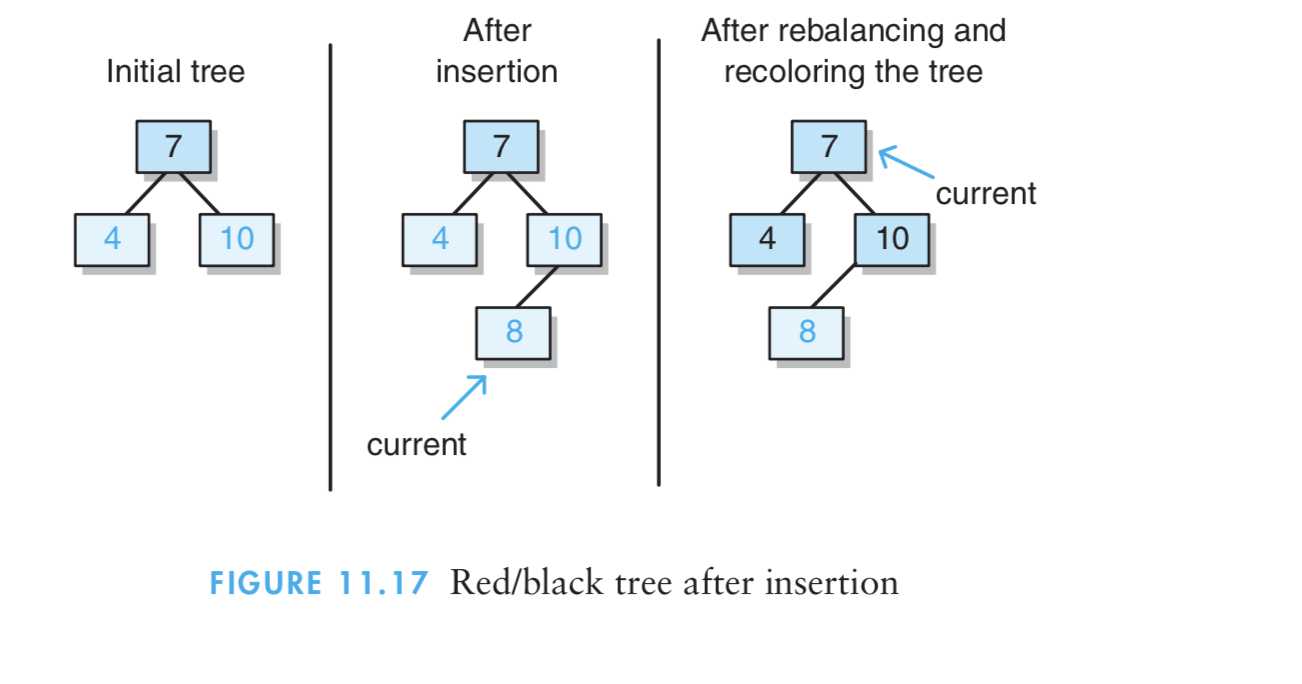
（4）红黑树中元素插入：
将一个节点插入到红黑树中，需要执行哪些步骤呢？首先，将红黑树当作一颗二叉查找树，将节点插入；然后，将节点着色为红色；最后，通过旋转和重新着色等方法来修正该树，使之重新成为一颗红黑树。详细描述如下：

1、第一步: 将红黑树当作一颗二叉查找树，将节点插入。
红黑树本身就是一颗二叉查找树，将节点插入后，该树仍然是一颗二叉查找树。也就意味着，树的键值仍然是有序的。此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。这也就意味着，任何的旋转和重新着色操作，都不会改变它仍然是一颗二叉查找树的事实。
好吧？那接下来，我们就来想方设法的旋转以及重新着色，使这颗树重新成为红黑树！

2、第二步：将插入的节点着色为"红色"。
为什么着色成红色，而不是黑色呢？为什么呢？在回答之前，我们需要重新温习一下红黑树的特性：

(1) 每个节点或者是黑色，或者是红色。

(2) 根节点是黑色。

(3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]

(4) 如果一个节点是红色的，则它的子节点必须是黑色的。

(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
将插入的节点着色为红色，不会违背"特性(5)"！少违背一条特性，就意味着我们需要处理的情况越少。接下来，就要努力的让这棵树满足其它性质即可；满足了的话，它就又是一颗红黑树了。o(∩∩)o...哈哈

3、第三步: 通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。
第二步中，将插入节点着色为"红色"之后，不会违背"特性(5)"。那它到底会违背哪些特性呢？
对于"性质(1)"，显然不会违背了。因为我们已经将它涂成红色了。
对于"性质(2)"，显然也不会违背。在第一步中，我们是将红黑树当作二叉查找树，然后执行的插入操作。而根据二叉查找数的特点，插入操作不会改变根节点。所以，根节点仍然是黑色。
对于"性质(3)"，显然不会违背了。这里的叶子节点是指的空叶子节点，插入非空节点并不会对它们造成影响。
对于"性质(4)"，是有可能违背的！
那接下来，想办法使之"满足特性(4)"，就可以将树重新构造成红黑树了。

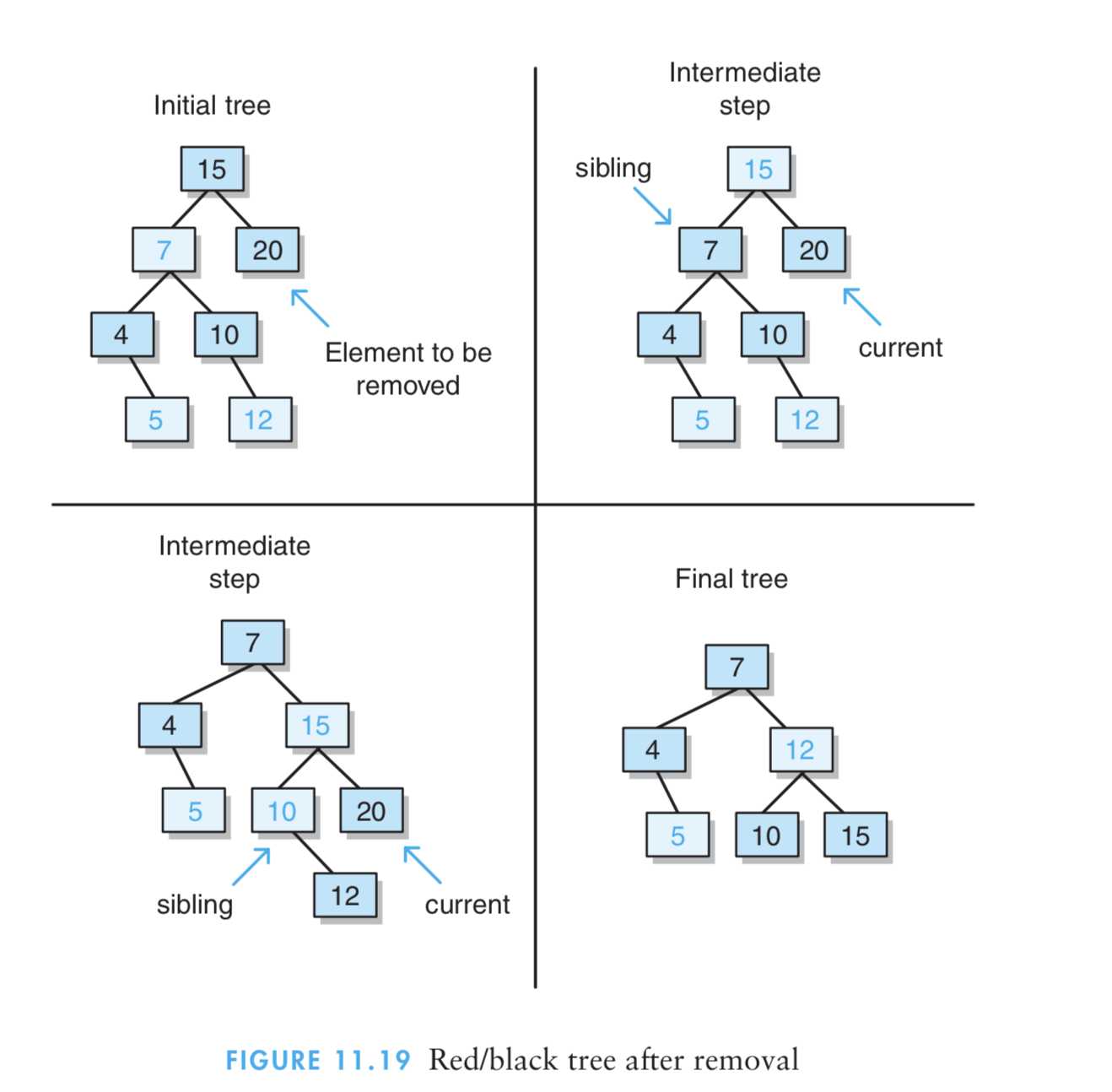
（5）红黑树中元素删除：
-（1）重新平衡化（及重新着色）：删除元素之后进行这一操作，是一种迭代过程，从删除点开始，一直上溯到树根。因此，如前所述，实现红黑树时最好在各个结点中包含一个父结点引用。这一过程的终止条件是（current==root）或（current.color==red），其中current是我们正在处理的这个结点。

• （2）在删除中而言，焦点要放在当前结点的兄弟的颜色上。
  • 如果兄弟的颜色是red，则在做其他事之前必须完成如此处理步骤：
    • （1）设置兄弟的颜色为black；
    • （2）设置current的父亲的颜色为red；
    • （3）让兄弟绕着current的父亲向右旋转；
    • （4）设置兄弟等于current的父亲的左孩子；
  • 如果兄弟的两个孩子都是black或null，则需要做到：
    • （1）设置兄弟的颜色为red；
    • （2）设置current等于current的父亲；
  • 如果兄弟的两个孩子不全为black，则将查看兄弟的左孩子是否是black。如果是，则在继续之前必须完成如下步骤：
    • （1）设置兄弟的右孩子的颜色为black；
    • （2）设置兄弟的颜色为red；
    • （3）让兄弟的右孩子绕着兄弟本身向右旋转。
    • （4）设置兄弟等于current的父亲的左孩子；
  • 最后是兄弟的两个孩子都不为black这一情况，这时必须：
    • （1）设置兄弟的颜色为current的父亲的颜色；
    • （2）设置current的父亲的颜色为black；
    • （3）设置兄弟的左孩子的颜色为black；
    • （4）让兄弟绕着current的父亲向右旋转；
    • （5）设置current等于树根。
  • 该循环终止之后，我们要删除该结点，并设置其父亲的孩子引用为null。
    

代码调试中的问题和解决过程

• 问题1：在补全代码的时候，发现有一个字段自己好像没有见过instanceof
• 问题1解决方案：
  （1）自己也查了查这个到底是什么？用法如下：
• 1、java 中的instanceof 是一个二元操作符（运算符）运算符，由于是字母组成，所以是Java的保留关键字，但是和>=，<=，==属同一类，它的作用是用来判断，instanceof 左边对象是否为instanceof 右边类的实例，返回一个boolean类型值。还可以用来判断子父类的所属关系。
• 2、用法：
  boolean result = object instanceof class
  参数：
  Result：布尔类型。
  Object：必选项。任意对象表达式。
  Class：必选项。任意已定义的对象类。
  说明：
  如果 object 是 class 的一个实例，则 instanceof 运算符返回 true。如果 object 不是指定类的一个实例，或者 object 是 null，则返回 false。

代码链接

上周考试错题总结

测试还没有结束

结对及互评

• 本周结对学习情况
  • 20172316赵乾宸
• 博客中值得学习的或问题：
  • 内容详略得当；
  • 代码调试环节比较详细；
• 基于评分标准，我给本博客打分：5分。得分情况如下：

1. 正确使用Markdown语法（加1分）：
2. 模板中的要素齐全（加1分）
3. 教材学习中的问题和解决过程, 一个问题加1分

4. 代码调试中的问题和解决过程, 一个问题加1分

   • 20172316唐才铭

• 博客中值得学习的或问题：
  • 内容详略得当；
  • 代码调试环节比较详细；
• 基于评分标准，我给本博客打分：9分。得分情况如下：

1. 正确使用Markdown语法（加1分）：
2. 模板中的要素齐全（加1分）
3. 教材学习中的问题和解决过程, 一个问题加1分
4. 代码调试中的问题和解决过程, 一个问题加1分

感悟

这一周很显然的感觉到自己时间很不够用，可能自己对于时间的分配还是有些不合理，总是做了些浪费时间的事情，也发现自己现在的时间观念没有过去那样很强了，希望自己可以经常反省，自己为什么会做事越来越慢。

学习进度条

参考资料

蓝墨云班课
Java程序设计
红黑树之原理和算法实现
java中instanceof的用法和实战
AVL树(平衡二叉树)
AVL树算法思想和代码实现
AVL树的旋转图解和简单实现

2018-2019-20172329 《Java软件结构与数据结构》第七周学习总结

标签：红色   必须   add   树的高度   开始   cti   contain   ceo   查找   

原文地址：https://www.cnblogs.com/qh45wangwenbin/p/9893609.html