算法的时间复杂度

标签：复杂   函数   n+2   alt   忽略   nlogn   形式   col   推理   

算法的时间复杂度

编写算法时，需要对算法进行分析。第一是从数学上证明算法的正确性，这一步主要用到形式化证明的方法及相关推理模式，如循环不变式、数学归纳法等。而在证明算法是正确的基础上，第二部就是分析算法的时间复杂度。这是用来衡量你的算法好不好，以及能不能用。这在算法的编写当中至关重要。因为时间复杂度可以帮助我们优化算法。也是衡量算法能否使用的判定条件。

时间复杂度的定义：

算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T（n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。 

时间复杂度的计算

 如果一个算法的执行次数是 T(n)，那么只保留最高次项，同时忽略最高项的系数后得到函数 f(n)，此时算法的时间复杂度就是 O(f(n))。为了方便描述，下文称此为 大O推导法。

该算法的执行次数为2N+2次，所以我们可以根据推导法计算出来，这个算法的时间复杂度为----------------O（n）

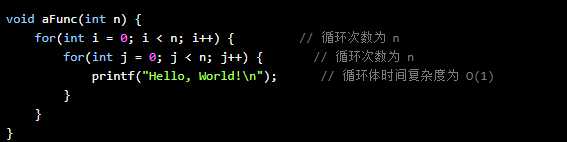
该算法的执行次数为N^2+2N次，所以我们可以根据推导法计算出来，这个算法的时间复杂度为----------------O（n^2）,这种循环结构可以用乘法判定也就是O(n × n × 1)

时间复杂度所耗费的时间是：

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) <O(2ⁿ) < O(n!) <O(nⁿ)

 时间复杂度的结论：

结论1：常见的算法的时间复杂度，

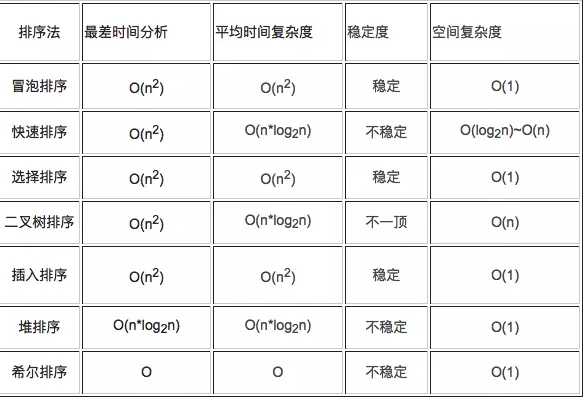
结论2：算法中语句执行次数为一个常数，则时间复杂度为O(1),

结论3：当你的算法的时间复杂度超过了O（n^2）时，你就要考虑这个算法的规模了，因为这会在后面增长的非常快而导致程序卡死

算法的时间复杂度

标签：复杂   函数   n+2   alt   忽略   nlogn   形式   col   推理   

原文地址：https://www.cnblogs.com/carsonche/p/9882216.html